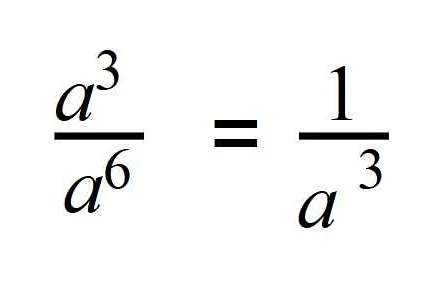10 в минус 3 степени: как правильно записать и что означает в математике

10 в минус 3 степени — это 0,001 в математике. Разберем формулу и примеры вычислений на странице. Получите ответ на вопрос в нашей статье!

10 в минус 3 степени — это очень маленькое число, которое используется в науке и математике для обозначения десятичных дробей, таких как 0,001 или 0,0001. Это число может быть записано как 0.001 или как 1/1000, а также может быть обозначено символом маленькой буквы «мю» (μ).

Существует несколько примеров того, как 10 в минус 3 степени может быть использовано в математике. Одним из таких примеров является вычисление единицы измерения массы — миллиграмма, которая равна 0,001 грамма. Другой пример включает вычисление единицы измерения сопротивления электрического тока — миллиома, которая равна 0,001 ома.

Чтобы более глубоко понять концепцию 10 в минус 3 степени и его использование в математике, необходимо ознакомиться со следующими формулами:

Десятичная дробь: 0,001 = 10-3
Обыкновенная дробь: 1/1000 = 10-3

В общем, 10 в минус 3 степени является важным числом в математике, науке и инженерии, и его использование приводит к созданию точных и удобных единиц измерения.

в минус 3 степени — что это за число?

В математике отрицательная степень числа означает, что это число является дробью с единицей в числителе и этим числом в знаменателе в положительной степени. Таким образом, 10 в минус 3 степени (10-3) равняется 1/1000 или 0,001.

Отрицательные степени удобно использовать в научных вычислениях, где может понадобиться работать с очень большими или маленькими числами. Например, для обозначения электрического сопротивления выраженного в омах, используются отрицательные степени числа 10, так как сопротивление может быть очень маленьким, например, 0,001 Ом.

Также, отрицательные степени удобно использовать для представления размеров и масс в научных и инженерных расчетах. Например, для измерения относительной громкости звука используются децибелы, которые являются отрицательными степенями числа 10.

В общем случае, если число возведено в отрицательную степень, то это будет дробью с числом в знаменателе в положительной степени. Например, 5 в минус 2 степени (5-2) равно 1/25 или 0,04.

Видео по теме:

Понятие и определение

10 в минус 3 степени — это одна тысячная или десятая десятичной дроби, обозначаемая математическим знаком м (-3) после числа 10.

Данный математический термин является частью системы международных стандартов СИ и используется для измерения единиц измерения, таких как миллиметры, микросекунды, миллиграммы, микроамперы и т. д.

При использовании научных обозначений, таких как физика, математика, химия, биология, технология, информатика, 10 в минус 3 степени означает доли единицы измерения, а не целые числа.

• Например, 1 километр — это 1000 метров, 1 микрофарад — это 0,000001 фарада, 1 миллимоль — это 0,001 моль.

Ведущие нули в записи таких дробных чисел могут быть опущены, если они не имеют значимого значения для описания исходного значения.

Например, 0.001 и .001 оба обозначают одну тысячную.

Как читать число 10 в минус 3 степени?

Чтение числа 10 в минус 3 степени может вызвать дополнительные вопросы, особенно у людей, которые не знакомы с науками, связанными с математикой и физикой. Тем не менее, данное число имеет очень простое и понятное значение:

• 10 в минус 3 степени равно 0,001 (единица на три нуля меньше 1).

Эту же информацию можно представить в следующем виде:

Число	Обозначение	Значение
10	-3	0.001

Таким образом, 10 в минус 3 степени означает, что число 1 разделено на 1000 (то есть, очень маленькое значение).

Важно понимать, что используя степени и экспоненты мы можем представить различные числа в удобной математической форме, но это не значит, что значения этих чисел становятся менее важными. Например, 10 в минус 3 степени может означать концентрацию раствора, скорость изменения чего-либо, мощность сигнала и т.д.

Вопрос-ответ:

Что такое «10 в минус 3 степени»?

«10 в минус 3 степени» означает 0,001. Это число образуется при возведении числа 10 в отрицательную третью степень.

Как записать «10 в минус 3 степени» в десятичном виде?

В десятичном виде «10 в минус 3 степени» записывается как 0,001.

Какая формула используется для возведения числа в отрицательную степень?

Для возведения числа в отрицательную степень используется формула a^-n = 1/(a^n), где «a» — число, а «n» — отрицательная степень.

Какое число образуется при возведении 2 в минус 4 степень?

При возведении 2 в минус 4 степень образуется число 0,0625.

Можно ли использовать отрицательные степени в других областях математики?

Отрицательные степени могут использоваться в различных областях математики, например, в алгебре, геометрии, математическом анализе и т.д.

Как возведение в отрицательную степень связано с инверсией?

Возведение в отрицательную степень связано с инверсией (обращением) числа. Например, если возвести число 2 в степень -1, то получится 1/2, что является инвертированной формой числа 2.

Как «10 в минус 3 степени» связано с научной нотацией?

Научная нотация используется для представления очень больших или очень маленьких чисел. Например, число 0,001 может быть записано в научной нотации как 1 x 10^-3.

Формула перевода числа 10 в минус 3 степени в десятичную систему

Число 10 в минус 3 степени (10-3) является очень маленьким числом, эквивалентным 0,001 в десятичной системе исчисления. Для перевода этого числа в десятичную систему можно использовать следующую формулу:

10-3 = 1 / 1000 = 0,001

Эта формула указывает, что 10 в минус 3 степени эквивалентно дроби 1/1000, которая также равна 0,001 в десятичной системе. Данный пример может быть использован, чтобы понять, как работает отрицательная степень числа 10.

Общая формула перевода

Для перевода чисел из одной системы счисления в другую с помощью степеней часто используется общая формула перевода:

• Пусть число A записано в системе счисления с основанием a.
• Требуется перевести число A в систему счисления с основанием b.
• Для этого число A нужно разложить на множители основания системы счисления b в виде:
  • A = cn*bn + cn-1*bn-1 + … + c1*b1 + c0*b0,
  • где n — количество знаков числа A в системе счисления b,
  • ci — цифры числа A в системе счисления b,
  • от младшего разряда к старшему.
• Значения ci могут быть вычислены по формуле:
  • ci = A mod bi+1 / bi,
  • где mod — операция остатка от деления.
• Таким образом, число A в системе счисления b будет записано в виде:
  • cncn-1…c1c0b.

Применение общей формулы перевода позволяет быстро и точно переводить числа из одной системы счисления в другую.

Примеры перевода в десятичную систему

Перевод числа из другой системы счисления в десятичную осуществляется по следующей формуле:

an-1*bn-1 + an-2*bn-2 + … + a1*b1 + a0*b0,

где

• an-1, an-2, …, a0 — цифры в исходном числе,
• b — основание системы счисления,
• n — количество разрядов в числе.

Например, для перевода числа 10112 (в двоичной системе счисления) в десятичную систему счисления, необходимо расчитать следующее значения:

• 1*23 + 0*22 + 1*21 + 1*20 = 8 + 2 + 1 = 11

Аналогично, для перевода числа 367 (в семеричной системе счисления) в десятичную систему счисления, получаем:

• 3*71 + 6*70 = 21 + 6 = 27

Таким образом, перевод чисел из других систем счисления в десятичную систему может быть осуществлен с помощью соответствующей формулы и базовых знаний работы с разрядами и степенями основания системы счисления.

ЧислоИсходная системаДесятичный эквивалент

10112	Двоичная	11
367	Семеричная	27
1234	Четверичная	27

Формула перевода числа 10 в минус 3 степени в другие системы счисления

Число 10 в минус 3 степени обозначается как 0.001 в десятичной системе счисления. Для перевода этого числа в другие системы счисления, необходимо знать формулу перевода.

Формула перевода числа 10 в минус 3 степени:

1. Умножаем число 0.001 на основание системы счисления, в которую нужно перевести число.
2. Записываем целую часть результата умножения в новую систему счисления.
3. Умножаем дробную часть результата умножения из первого пункта на основание системы счисления.
4. Записываем целую часть нового результата умножения в новую систему счисления.
5. Повторяем шаги 3-4 до тех пор, пока дробная часть не станет равной нулю или до тех пор, пока не будет получено необходимое количество знаков после запятой.

Например, для перевода числа 0.001 в двоичную систему счисления:

ШагРезультат

1	0.001 * 2 = 0.010
2	0

Таким образом, число 0.001 в десятичной системе счисления равняется 0 в двоичной системе счисления.

Перевод в двоичную систему счисления

В компьютерной технике и программировании используется двоичная система счисления. В двоичной системе счисления числа состоят только из двух символов 0 и 1. Чтобы перевести число из десятичной системы счисления в двоичную, нужно разделить число на 2 и записывать остатки, пока не получим 0.

Пример:

Перевести число 31 в двоичную систему счисления

1. 31 ÷ 2 = 15, остаток 1
2. 15 ÷ 2 = 7, остаток 1
3. 7 ÷ 2 = 3, остаток 1
4. 3 ÷ 2 = 1, остаток 1
5. 1 ÷ 2 = 0, остаток 1

Чтобы получить двоичную запись числа 31, нужно записать остатки снизу вверх: 11111

Также можно использовать таблицу степеней двойки:

СтепеньЗначение

2^4	16
2^3	8
2^2	4
2^1	2
2^0	1

Для перевода числа в двоичную систему можно использовать таблицу степеней двойки. Например, для числа 10 нужно выбрать степени, которые в сумме дают 10: 2^3, 2^1. В двоичной системе это будет выглядеть как 1010.

Перевод в восьмеричную систему счисления

Восьмеричная система счисления основана на использовании 8 цифр: 0, 1, 2, 3, 4, 5, 6 и 7. Числа в восьмеричной системе записываются в формате N8, где N — любое целое положительное число. Важно заметить, что одна цифра в восьмеричной системе эквивалентна трем битам в двоичной системе.

Перевод числа из десятичной системы в восьмеричную происходит путем деления числа на 8 с последующей записью остатка. Этот процесс повторяется до тех пор, пока результат деления не станет меньше 8.

Например, для перевода числа 95 в восьмеричную систему счисления:

1. Делим 95 на 8: 95 ÷ 8 = 11, остаток 7
2. Делим 11 на 8: 11 ÷ 8 = 1, остаток 3
3. Результат уже меньше 8, поэтому оставляем его: 1

Таким образом, число 95 в восьмеричной системе записывается как 137, где каждая цифра обозначает остаток при делении числа на 8.

Перевод в шестнадцатеричную систему счисления

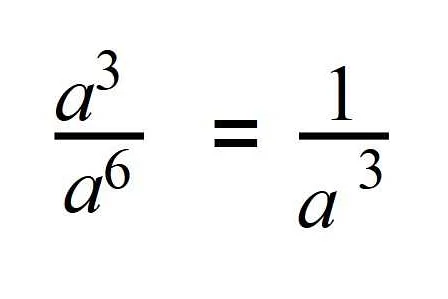
Шестнадцатеричная система счисления имеет основание 16 и использует цифры от 0 до 9 и буквы от A до F (или a до f) для обозначения чисел. При переводе числа в шестнадцатеричную систему счисления, каждая группа из 4 двоичных цифр заменяется на соответствующую шестнадцатеричную цифру.

Например, число 10110101 в двоичной системе счисления может быть переведено в шестнадцатеричную систему следующим образом:

• Разделим число на группы по 4 цифры: 1011 0101
• Заменим каждую группу на соответствующую шестнадцатеричную цифру: B5

Таким образом, число 10110101 в двоичной системе счисления эквивалентно числу B5 в шестнадцатеричной системе счисления.

Другой пример: число 1101110010 в двоичной системе счисления может быть переведено в шестнадцатеричную систему счисления следующим образом:

• Разделим число на группы по 4 цифры: 1101 1100 10
• Заменим каждую группу на соответствующую шестнадцатеричную цифру: DС2

Итак, число 1101110010 в двоичной системе счисления эквивалентно числу DC2 в шестнадцатеричной системе счисления.

Значение числа 10 в минус 3 степени в математических выражениях

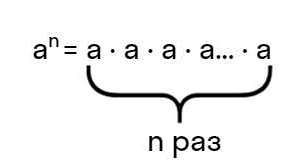
10 в минус 3 степени — это дробь, где верхнее число равно единице, а нижнее — 10 в третьей степени. В математической записи это можно представить как 1/10^3.

Также 10 в минус 3 степени можно записать в десятичной форме, что даст значение 0.001. Это число является долей единицы и принадлежит к классу дробных чисел, которые записываются через точку.

В технической и научной нотации часто используется степень десяти. Числа, записанные в формате 10 в отрицательной степени, сильно малы и часто связаны с физическими и химическими константами.

Например, в механике 10 в минус 3 степени можно использовать для измерения массы микрограму (1 мкг = 0,000001 кг).

Таким образом, значение числа 10 в минус 3 степени может быть представлено как дробь, десятичная дробь или через использование степеней числа 10 в научной нотации. Оно является особенно важным в научных расчетах, а также в различных областях, где необходимо работать с малыми значениями.

Примеры математических выражений

1. Если умножить число 5 на 10 в минус 3 степени, то получится 0.005:

5 x 10-3 = 0.005

2. Рассмотрим выражение (3 + 2) x 4. Сначала нужно выполнить действие в скобках, а затем умножить на 4:

(3 + 2) x 4 = 5 x 4 = 20

3. Попробуем найти площадь круга с радиусом 2 см. Для этого воспользуемся формулой площади круга:

S = πr2 = 3.14 x 22 = 3.14 x 4 = 12.56

Таким образом, площадь круга с радиусом 2 см будет равна 12.56 см2.

4. Найдем корни квадратного уравнения 2×2 — 7x + 3 = 0:

Сначала вычислим дискриминант:

D = b2 — 4ac = 49 — 24 = 25

Корни уравнения находим по формуле:

x1, x2 = (-b ± √D) / 2a

x1, x2 = (7 ± 5) / 4

Ответ:

• x1 = 3/2
• x2 = 1/2

5. Предположим, что мы хотим расчитать популяцию города, зная только число жителей на единицу площади и общую площадь города. Для этого нужно умножить число жителей на единицу площади на общую площадь города:

Популяция = число жителей на единицу площади x общая площадь

Пример: Если на единицу площади приходится 10 человек, а общая площадь города составляет 100 км2, то популяция города будет равна 10 x 100 000 000 = 1 000 000 человек.

Применение числа 10 в минус 3 степени в различных областях

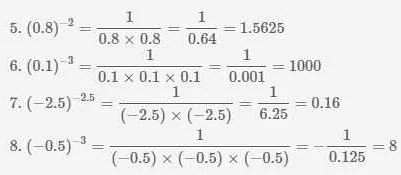
Число 10 в минус 3 степени равно 0.001. Это очень маленькое число, но оно находит широкое применение в различных областях, включая науку, технологии и финансы.

В науке 10 в минус 3 степени используется для измерения малых единиц, например, величина атомной массы измеряется в атомных единицах массы (a.m.u), которые равны 0.001 массы атома углерода-12. Также, 0.001 литра называется 1 миллилитром (мл) и используется для измерения объема жидкости.

В технологиях число 10 в минус 3 степени используется для измерения малых величин, например, в диапазоне частот 0.001 Гц – 1 кГц. Кроме того, стандарт гигабитного Ethernet использует передачу данных со скоростью 1 Гбит/с, что означает, что каждую секунду передается 10 в 9 степени бит, а каждый бит составляет 10 в минус 3 степени секунды.

В финансах 10 в минус 3 степени используется для измерения денежных единиц. Например, 1 пипс (точка) при торговле на валютном рынке означает изменение курса на 0.0001. Также, 1 базисный пункт (BPS) при изменении процентной ставки равен 0,01 процента.

Таким образом, число 10 в минус 3 степени — это маленькое число, но важное и широко используемое в различных областях науки, технологий и финансов.

Использование в физике

Десять в минус третьей степени — это очень маленькое число, которое часто используется в физике для измерения очень маленьких величин.

Например, одна из основных констант в физике — постоянная Планка — выражается в Джоулях на секунду, умноженных на десять в минус 34 степени.

Также десять в минус третьей степени используется для измерения электрического заряда, когда электрический заряд одного электрона равен примерно 1,6 × 10 в минус 19 степени Кулона.

Термин «нанометр» также используется в физике для измерения длин, он равен миллионной части миллиметра, то есть десяти в минус девятой степени метра.

Использование десяти в минус третьей степени часто встречается в физике элементарных частиц и атомной физике, где очень маленькие величины являются нормой.

Использование в технологии

10 в минус 3 степени — это дробь, в которой числитель равен единице, а знаменатель равен десяти в третьей степени. В математике это означает, что данное число равно 0.001.

Однако, значение 10 в минус 3 степени имеет широкое применение в технологии. Например, часто используется в электронике для обозначения маленьких единиц измерения, таких как микросекунды (10 в минус 6 степени) или нанометры (10 в минус 9 степени).

Также значение 10 в минус 3 степени активно используется в компьютерной науке и программировании. Например, при измерении времени выполнения программы используется миллисекунда (10 в минус 3 степени секунды). Кроме того, многие программисты используют метрическую систему счисления, где 1 Кбайт (килобайт) равен 1000 байт, в отличие от стандартной системы счисления, где 1 Кбайт равен 1024 байтам. Это связано с тем, что многие компьютерные системы используют значениe 10 в минус 3 степени, чтобы показать размер файлов.

Использование значения 10 в минус 3 степени находит свое применение не только в технологии, но и в других сферах. Например, в физике это значение используется для обозначения милливольт (10 в минус 3 степени Вольта) или миллиампер (10 в минус 3 степени Ампера).

Использование в информатике

В информатике часто встречаются значения, выраженные в 10 в минус 3 степени. Особенно это часто используется в измерениях единиц информации, таких как байты, килобайты, мегабайты и т.д. Например, 1 килобайт равен 1024 байтам, что можно записать как 2 в 10 степени.

Также 10 в минус 3 степени часто используется в рассчетах времени выполнения компьютерных программ. Время можно измерять в миллисекундах (10 в минус 3 степени секунды) или микросекундах (10 в минус 6 степени секунды).

В математических вычислениях 10 в минус 3 степени иногда используется для обозначения числа, близкого к нулю. Например, 0.001 можно записать как 10 в минус 3 степени.

• Примеры использования в информатике:
• — Размер файлов
• — Частота процессора
• — Вычислительные мощности
• — Время выполнения программ

Таким образом, понимание значения 10 в минус 3 степени является важным для понимания многих информационных технологий и вычислительных процессов.