Чего нельзя делать в математике

В статье представлены основные ошибки, которые могут быть допущены в математике. Узнайте, чего нельзя делать при работе с числами, формулами и графиками, чтобы избежать путаницы и получить правильный результат.

Математика — это наука, которая требует точности и логики. Однако, даже самые опытные математики иногда допускают ошибки и попадают в заблуждения. Это может происходить по разным причинам — невнимательность, неправильное применение методов или просто непонимание определенных понятий.

Одна из наиболее распространенных ошибок в математике — это неправильное использование знаков операций, таких как плюс, минус, умножение и деление. Например, некоторые люди ошибочно считают, что умножение всегда должно выполняться перед сложением или вычитанием, что приводит к неправильным результатам. Также, часто встречаются ошибки в расстановке скобок, что может изменить значение выражения.

Важно помнить, что порядок операций в математике определен и должен быть соблюден, чтобы получить правильный ответ.

Еще одним распространенным заблуждением в математике является идея о том, что все числа — рациональные. Некоторые люди могут быть уверены, что все числа можно представить в виде обыкновенной дроби. Однако, это не так. Существуют так называемые иррациональные числа, которые не могут быть представлены в виде дроби. Например, число «пи» (π) или квадратный корень из 2 являются иррациональными числами.

Важно помнить, что математика — это наука, которая строится на логике и точности. Избегайте ошибок и заблуждений, будьте внимательны при выполнении операций и понимайте правильное использование математических понятий. И помните, что ошибки и заблуждения — это нормальная часть обучения и развития в математике. Главное — учиться на своих ошибках и постоянно совершенствоваться.

Ошибки и заблуждения в математике: избегайте их

1. Ошибки в расчетах: Одна из наиболее распространенных ошибок в математике — это ошибки в расчетах. Это может быть вызвано невнимательностью, опечатками или неправильными формулами. Чтобы избежать таких ошибок, важно внимательно проверять каждый шаг расчета и использовать калькулятор или компьютер, если это необходимо.

2. Неправильное понимание понятий: В математике много понятий, которые могут быть неправильно поняты. Например, многие люди неправильно понимают понятие «бесконечность». Они могут считать, что бесконечность — это число или что она может быть измерена. Однако в математике бесконечность — это абстрактное понятие, которое указывает на то, что некоторое количество или процесс не имеет конца или границы.

3. Использование неправильных методов: В математике существует множество методов и подходов для решения различных задач. Ошибкой является использование неправильных методов или неправильных формул. Например, использование метода сложения для умножения или деления чисел является ошибкой. Чтобы избежать таких ошибок, важно хорошо знать основные математические методы и формулы.

4. Недостаточное объяснение шагов: При решении математических задач важно не только получить правильный ответ, но и правильно объяснить каждый шаг решения. Недостаточное объяснение шагов может привести к непониманию или неправильному пониманию процесса решения задачи. Чтобы избежать этой ошибки, важно включать все необходимые пояснения и промежуточные вычисления в своем решении.

5. Не проверять результат: Последняя ошибка, которую следует избегать в математике, — это не проверять полученный результат. Ошибки могут возникать в любом месте решения задачи, поэтому важно всегда проверять правильность своих вычислений и ответов. Это можно сделать путем повторного решения задачи или использования альтернативных методов.

Избегание этих ошибок и заблуждений поможет вам стать более уверенным в своих математических навыках и предотвратить возможные ошибки в будущем.

Неправильное понимание основных понятий

Например, многие люди неправильно интерпретируют понятие «равенства». Они считают, что знак «равно» означает, что два объекта абсолютно идентичны. Однако в математике «равенство» означает только то, что два объекта имеют одно и то же значение. Таким образом, равные числа могут быть представлены разными символами или записаны в различных формах, но они все равно будут равными.

Другим распространенным заблуждением является неправильное понимание понятия «функция». Многие люди думают, что функция — это просто выражение или формула. Однако на самом деле функция — это отображение множества одних элементов (аргументов) в другое множество элементов (значений), которое удовлетворяет определенным правилам. Функция может быть представлена различными способами, включая графики, таблицы или формулы, но само понятие функции намного шире, чем просто выражение или формула.

Кроме того, неправильное понимание понятий «предел» и «бесконечность» также может привести к ошибкам. Многие люди думают, что предел — это просто значение, к которому стремится последовательность или функция. Однако предел — это более сложное понятие, которое имеет строгие математические определения. Аналогично, бесконечность — это не просто большое число, а математическое понятие, которое обозначает отсутствие конечного значения или предела.

Важно понимать основные понятия в математике правильно, чтобы избежать ошибок и заблуждений. Неправильное понимание может привести к неправильным выводам и неправильным решениям задач. Поэтому рекомендуется уделить достаточно времени и внимания изучению основных понятий и их определений, чтобы иметь правильное представление о математике.

Пренебрежение порядком операций

Одна из наиболее распространенных ошибок, совершаемых в математике, связана с пренебрежением порядком операций.

Часто люди просто производят арифметические операции слева направо, не учитывая приоритет операций и правила расстановки скобок. Это приводит к неправильным результатам и искажению математических выражений.

Например, рассмотрим следующее выражение: 2 + 3 * 4. Если мы проигнорируем порядок операций и просто сложим 2 и 3, а затем умножим результат на 4, получим неправильный ответ 20. Однако, согласно правилам математики, сначала нужно выполнить умножение (3 * 4), а затем сложение (2 + 12), что дает правильный ответ 14.

Пренебрежение порядком операций также может привести к ошибкам при вычислении сложных выражений, содержащих различные операции: сложение, вычитание, умножение, деление и возведение в степень. В таких случаях важно следовать правилам приоритета операций и использовать скобки для явного указания порядка выполнения операций.

Избегая пренебрежения порядком операций, можно избежать множества ошибок и убедиться в правильности математических вычислений.

Помните: порядок операций — важная составляющая математики!

Неправильное приоритетное расположение скобок

Когда вы работаете с выражением, важно правильно расставить скобки, чтобы указать, какие операции должны быть выполнены в первую очередь. Неправильное расположение скобок может привести к неправильному порядку операций и, следовательно, к неправильному ответу.

Например, рассмотрим следующее выражение:

2 + 3 * 4

Если мы неправильно расставим скобки, например, так:

(2 + 3) * 4

То мы получим неправильный результат: 20 вместо правильного ответа 14. Правильное расположение скобок в этом выражении должно быть:

2 + (3 * 4)

Правильное расставление скобок в математике важно для получения правильных результатов. Ошибки в расположении скобок могут привести к неправильным ответам и затруднить понимание математических концепций.

Поэтому, при работе с выражениями, всегда следует внимательно проверять правильность расположения скобок и убедиться, что они указывают на нужные операции.

Использование неверных формул и теорем

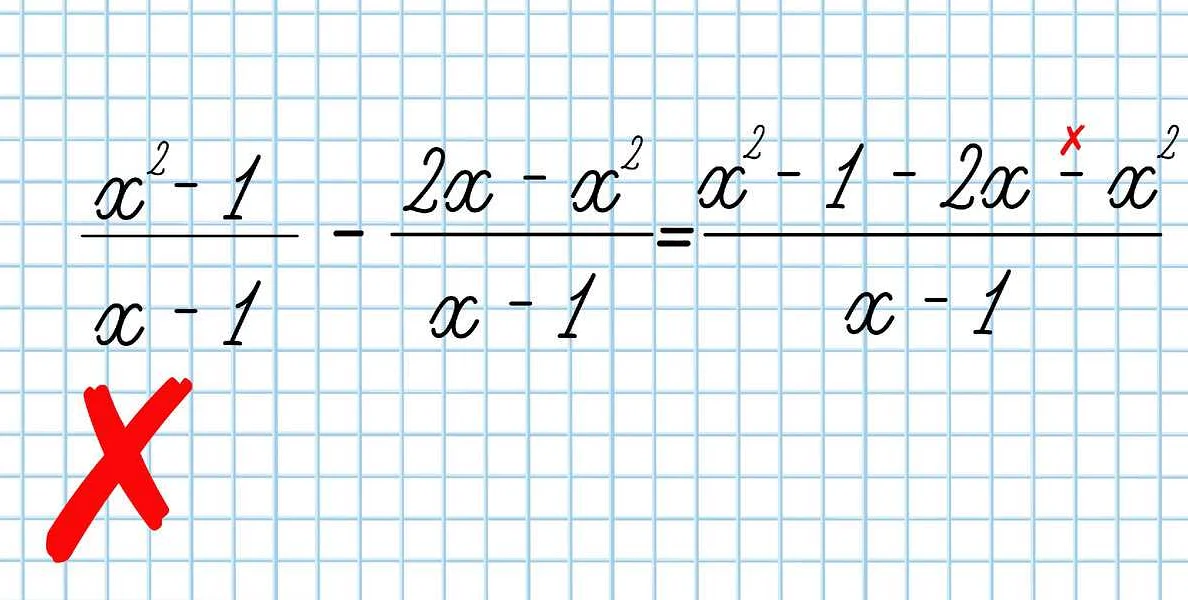
Важно помнить, что математика основана на логике и строгих математических доказательствах. Использование неправильных формул и теорем может привести к некорректным выводам и ошибкам в решении задач.

При изучении математики необходимо быть внимательным и аккуратным при применении формул и теорем. Важно проверять их правильность и убеждаться, что они соответствуют решаемой задаче.

Ошибки в использовании формул и теорем могут произойти по разным причинам. Некоторые из них могут быть связаны с неправильным пониманием математических концепций, неправильной интерпретацией условия задачи или неверным применением математических операций.

Для избежания ошибок в использовании формул и теорем необходимо тщательно изучать материал, проверять свои решения и консультироваться с преподавателем в случае сомнений. Также полезно использовать дополнительные математические источники для проверки правильности формул и теорем.

ОшибкиПримеры

Неправильное применение формулы	Использование формулы для расчета площади круга вместо формулы для расчета площади прямоугольника
Использование неверной теоремы	Применение теоремы Пифагора для треугольника, не являющегося прямоугольным
Неправильное понимание формулы или теоремы	Неправильное использование формулы для нахождения среднего арифметического

Использование неверных формул и теорем может привести к серьезным ошибкам и неправильным результатам. Поэтому важно быть внимательным и тщательно проверять правильность применяемых математических концепций.

Некорректное округление чисел

Одной из распространенных ошибок является округление только до определенного знака после запятой. Например, округление числа 3.14159 до двух знаков после запятой дает результат 3.14. Однако, если использовать этот результат для дальнейших вычислений, то можно получить неточный ответ. Например, при умножении числа 3.14 на 2 получится 6.28, в то время как правильный ответ равен 6.29.

Еще одной ошибкой является округление по правилу «ближайшего четного». Это правило гласит, что если десятичная часть числа равна 0.5, то число округляется до ближайшего четного. Например, число 2.5 округляется до 2, а число 3.5 округляется до 4. Однако, это правило приводит к неточности в вычислениях. Например, если округлить число 1.5 до ближайшего четного и затем прибавить 1, то получится 3, в то время как правильный ответ равен 2.

Для избежания ошибок при округлении чисел необходимо использовать правила математического округления. При округлении числа с десятичной частью 0.5, оно округляется до ближайшего целого числа с бо́льшей абсолютной величиной. Например, число 2.5 округляется до 3, а число 3.5 округляется до 4. Правило математического округления позволяет получить более точные результаты и избежать неточностей в вычислениях.

Некорректное округлениеПравильное округление

3.14159 округлено до 2 знаков после запятой: 3.14	3.14159 округлено до 2 знаков после запятой с математическим округлением: 3.15
1.5 округлено до ближайшего четного: 2	1.5 округлено с математическим округлением: 2

Недостаточное использование контрольных вычислений

Очень важно не только правильно решить задачу, но и проверить свое решение. Использование контрольных вычислений помогает обнаружить возможные ошибки в решении и исправить их. Контрольные вычисления могут быть самыми простыми — например, подстановка найденного значения обратно в исходное уравнение или простая проверка арифметических операций.

Недостаток контрольных вычислений может привести к серьезным ошибкам и заблуждениям в математике. Отсутствие контроля может привести к неправильным результатам, которые могут быть приняты за правильные. Такие ошибки могут привести к дальнейшим недопониманиям и затруднениям в процессе изучения математики.

Поэтому, чтобы избежать ошибок и заблуждений в математике, необходимо всегда проводить контрольные вычисления, чтобы удостовериться в правильности своих решений. Не стоит полагаться только на интуицию или оценку, а лучше всего проводить дополнительные вычисления для проверки.

Например, при решении уравнения следует всегда проверять найденное решение, подставляя его обратно в исходное уравнение и убедившись, что обе части равны.

Помните, что контрольные вычисления являются важной частью процесса решения математических задач и помогают избежать ошибок и заблуждений.

Видео по теме:

Вопрос-ответ:

Часто ли люди совершают ошибки в математике?

Ошибки в математике встречаются довольно часто, особенно у начинающих учеников. Даже опытные математики иногда делают ошибки, так как математика требует точности и внимательности.

Какие ошибки наиболее распространены в математике?

Среди наиболее распространенных ошибок в математике можно выделить неправильное понимание основных математических понятий, неправильное применение формул и правил, ошибки в расчетах, неверное чтение и запись чисел и символов.

Какие заблуждения часто возникают в математике?

В математике часто возникают заблуждения, связанные с неправильным пониманием математических понятий, например, путание понятий «равно» и «подобно», неверное умозаключение на основе одного примера, неправильное применение правил и формул. Также некоторые люди могут заблуждаться, полагая, что математика не имеет никакого отношения к реальному миру и является бесполезной.

Какие последствия могут быть от ошибок в математике?

Ошибки в математике могут привести к неправильным результатам расчетов или решению задач, что может повлечь за собой ошибки в других областях, например, в физике или экономике. Ошибки также могут привести к неправильному пониманию математических концепций, что может затруднить учебу и понимание более сложных математических тем.

Как можно избежать ошибок в математике?

Для избежания ошибок в математике важно быть внимательным и точным при решении задач, проверять свои расчеты и умозаключения, использовать правильные формулы и правила, а также консультироваться с учителем или другими математиками при возникновении затруднений. Также полезно практиковаться в решении разнообразных математических задач и примеров.

Какие ошибки и заблуждения следует избегать в математике?

В математике следует избегать различных ошибок и заблуждений, таких как неправильное применение формул, неправильное чтение условия задачи, неправильное округление чисел и т.д. Важно быть внимательным, аккуратным и точным при выполнении математических операций.

Неправильное использование пропорций и процентов

В математике, пропорции и проценты часто используются для расчетов и анализа данных. Однако, неправильное использование этих концепций может привести к ошибкам и недостоверным результатам.

Одной из распространенных ошибок является неправильное применение пропорций. Пропорция — это равенство двух отношений, которое можно представить в виде a:b = c:d. Ошибка возникает, когда пропорция не учитывает контекст или не соответствует реальной ситуации. Например, если у нас есть пропорция «10 яблок:5 апельсинов = 20 яблок:?», неправильно будет сделать вывод, что «?» равно 10 апельсинам, так как в данном контексте это не имеет смысла.

Другой распространенной ошибкой является неправильное использование процентов. Процент — это способ представления доли чего-либо в виде сотых долей. Ошибка возникает, когда процент используется некорректно или неправильно интерпретируется. Например, если мы говорим, что «80% студентов сдали экзамен успешно», это не означает, что оставшиеся 20% студентов провалили экзамен. Вероятно, они могли получить неудовлетворительные оценки или не явились на экзамен. Неправильная интерпретация процентов может привести к неверным выводам и недостоверным данным.

Чтобы избежать ошибок и заблуждений, связанных с использованием пропорций и процентов, важно тщательно анализировать контекст и учитывать все факторы, которые могут влиять на результат. Также следует использовать реалистичные и точные данные для расчетов и интерпретации процентов.

Завышенная уверенность в своих рассуждениях

Когда мы решаем задачу или доказываем теорему, мы должны быть критичными к нашим собственным аргументам и выводам. Завышенная уверенность может привести к неправильным результатам и ошибочным заключениям.

Часто завышенная уверенность возникает из-за недостатка опыта или неправильного понимания математических понятий и методов. Мы можем быть уверены в правильности нашей логики, но если мы не учитываем все возможные случаи или не используем правильные математические инструменты, то наши рассуждения могут быть неверными.

Чтобы избежать завышенной уверенности, необходимо всегда проверять свои рассуждения и результаты. Проверьте, соответствуют ли они математическим правилам и логике. Обращайте внимание на допущенные предположения и ограничения. Если вы не уверены в правильности своих рассуждений, не стесняйтесь обратиться за помощью к преподавателю или коллегам.

Завышенная уверенность в своих рассуждениях может привести к серьезным проблемам в математике. Ошибки могут быть сложно обнаружить и исправить, особенно если мы не подвергаем свои рассуждения критическому анализу. Поэтому всегда помните о важности скептицизма и самокритики в математике.