Чем математический термин отличается от понятия

Статья объясняет разницу между математическим термином и понятием, указывая на их сходства и отличия. Она рассматривает, что представляет собой каждое из этих понятий и как они применяются в математике.

Математический термин — это специальное слово или набор символов, которые используются в математике для обозначения определенного понятия или операции. Он обладает строгим определением и имеет точное значение в рамках математической теории. Математические термины обычно используются для описания числовых отношений, геометрических фигур, алгебраических операций и других математических концепций.

Понятие — это более широкое понятие, которое включает в себя все обобщенные представления о объектах, явлениях или идеях. Понятия не всегда имеют строгое определение и могут быть основаны на интуитивном понимании или личном опыте. Они могут быть субъективными и варьироваться в разных контекстах и областях знания. Понятия могут иметь более широкий спектр значений и использоваться для описания различных аспектов реального мира.

Например, математический термин «производная» имеет точное определение в рамках математического анализа. Он обозначает скорость изменения функции в каждой точке ее определения. С другой стороны, понятие «изменение» может использоваться в более широком контексте и описывать любые виды изменений, например, изменение погоды или изменение цвета вещей.

Важно отличать математические термины от понятий, чтобы избежать путаницы и неоднозначности в общении. Умение четко определять и использовать математические термины помогает устанавливать точные и ясные связи между понятиями и способствует развитию математического мышления и решения проблем.

Определение математического термина

Математические термины обладают определенными характеристиками, которые отличают их от обычных понятий:

ХарактеристикаОписание

Точность	Математические термины имеют строгое и точное определение, которое исключает неоднозначность или двусмысленность.
Объективность	Математические термины имеют однозначное значение, которое не зависит от личных суждений или толкований.
Универсальность	Математические термины используются во всех областях математики и применимы в различных контекстах и задачах.

Примеры математических терминов включают:

• Число — абстрактный математический объект, который представляет собой конкретное количество или величину.
• Функция — математическое правило, которое связывает каждый элемент одного множества с элементом другого множества.
• Матрица — упорядоченный прямоугольный массив элементов, расположенных в виде таблицы.
• Дифференциал — малая разность между значениями функции в бесконечно близких точках.

Определение понятия

В отличие от математического термина, понятие шире и может иметь несколько различных интерпретаций в разных контекстах. Оно может быть более гибким и вариативным, позволяя учитывать разные аспекты и перспективы.

Например, понятие «любовь» может иметь разные толкования в разных культурах или в различных областях знания, таких как психология, философия или литература. Каждое толкование отражает определенные аспекты этого понятия, но в целом оно описывает общую идею эмоциональной привязанности и привлечения к другому человеку.

Понятия можно классифицировать и организовывать в иерархические структуры или системы, чтобы лучше понять их взаимосвязи и сходства. Например, понятие «животные» может включать в себя более узкие понятия, такие как «кошки», «собаки» или «птицы». Классификация понятий помогает организовать знания и облегчает понимание сложных концепций.

Разница между математическим термином и понятием

Понятие — это более общий термин, который описывает идею, представление или концепцию о чем-то. Понятия могут быть более размытыми и не иметь такой точной формулировки, как математические термины. Они могут использоваться в разных контекстах и областях знаний.

В математике, термины используются для определения и обозначения определенных математических объектов и связей между ними. Например, термин «функция» используется для обозначения отображения, которое каждому элементу из одного множества ставит в соответствие элемент из другого множества. Это является математическим термином, который имеет строгое определение и используется в математических доказательствах и рассуждениях.

С другой стороны, понятия, такие как «число», «геометрия» или «вероятность», более общие и используются для описания широкого спектра математических идей и концепций. Они могут включать в себя различные термины и идеи, которые связаны с определенным понятием.

Таким образом, разница между математическим термином и понятием заключается в их уровне точности и специфичности. Математические термины имеют строгое определение и используются для обозначения конкретных математических объектов, в то время как понятия являются более общими и описывают идеи и концепции в широком контексте.

Примеры математических терминов

Ниже приведены некоторые примеры математических терминов:

• Аксиома: неотъемлемое основное предположение, которое принимается без доказательства и используется для вывода других утверждений.
• Функция: математическое правило, которое связывает каждый элемент одного множества с элементом другого множества.
• Матрица: прямоугольная таблица чисел или символов, разделенных на строки и столбцы, используемая для решения систем линейных уравнений и других математических операций.
• Интеграл: математический объект, обратный операции дифференцирования, который используется для вычисления площади под кривой или нахождения среднего значения функции.
• Вектор: математический объект, который имеет магнитуду и направление и используется для представления физических величин, таких как скорость и сила.

Это лишь некоторые примеры математических терминов, которые широко используются в различных областях математики и ее приложений.

Примеры понятий

Вот несколько примеров понятий:

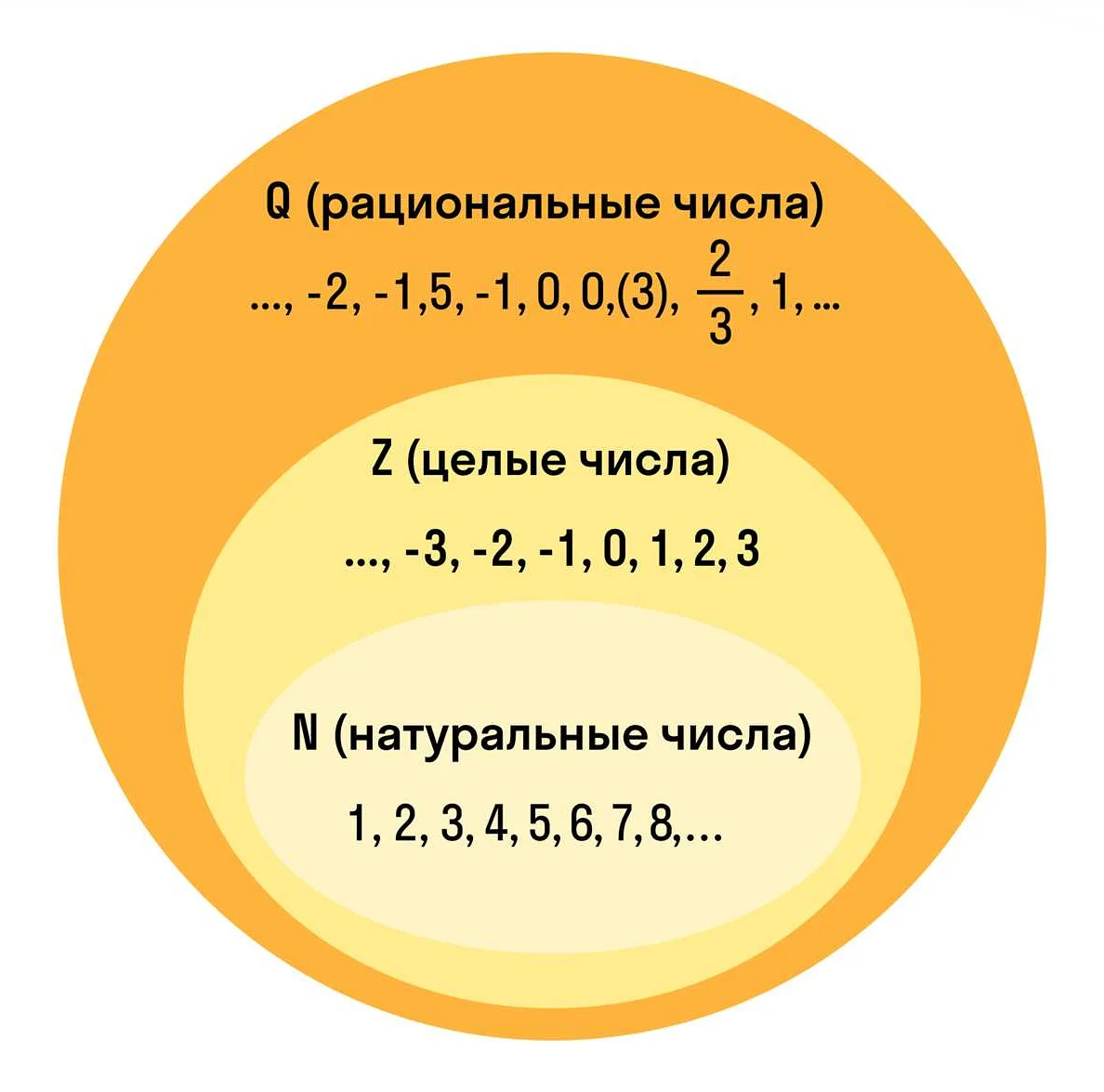
• Понятие «число» в математике означает абстрактную концепцию, представляющую определенное количество или размер. Примеры чисел включают натуральные числа (1, 2, 3), целые числа (-3, -2, -1, 0, 1, 2, 3), рациональные числа (1/2, 0.75) и иррациональные числа (π, √2).
• Понятие «функция» в математике представляет собой связь между двумя множествами, где каждому элементу первого множества сопоставлено ровно одно значение из второго множества. Примером функции может быть уравнение y = 2x, где каждому значению x сопоставляется значение y, равное удвоенному значению x.
• Понятие «граф» в математике описывает структуру, состоящую из вершин и ребер, которые соединяют эти вершины. Графы могут использоваться для моделирования связей между объектами. Например, граф может представлять сеть дорог, где вершины — это перекрестки, а ребра — дороги, соединяющие перекрестки.
• Понятие «матрица» в математике представляет собой двумерный массив чисел, обычно упорядоченных в виде таблицы. Матрицы используются для представления и решения систем уравнений, а также для описания преобразований в линейной алгебре. Например, матрица 2×2 может выглядеть следующим образом: [ [1, 2], [3, 4] ].

Значимость математических терминов

Математические термины играют важную роль в понимании и изучении математики. Они представляют собой специальные термины, используемые для описания математических объектов, операций и свойств. Знание и понимание математических терминов необходимо для участия в математических дискуссиях, чтения математических текстов и решения математических задач.

Одной из главных особенностей математических терминов является их точность и четкость. Каждый математический термин имеет строгое определение, которое исключает двусмысленность и неопределенность. Это позволяет ученым и математикам общаться на языке математики и быть уверенными в том, что их идеи и рассуждения будут поняты и оценены правильно.

Математические термины также помогают структурировать знания и организовать математическую информацию. Они позволяют классифицировать и группировать математические объекты по их свойствам и характеристикам. Например, термин «прямоугольник» описывает класс фигур, у которых все углы равны 90 градусов. Это позволяет нам сразу же сделать выводы и применять знания о прямоугольниках при решении задач и проблем.

Без математических терминов общение и обмен математической информацией были бы очень трудными и неэффективными. Использование математических терминов позволяет ученым и математикам точно и ясно выражать свои мысли и идеи. Кроме того, математические термины являются основой для формулирования математических теорем, законов и правил, которые играют важную роль в развитии математики и ее приложениях в других науках и областях жизни.

Важно отметить, что математические термины могут быть сложными и непонятными для неподготовленных людей. Однако, с помощью обучения и практики, каждый может научиться понимать и использовать математические термины. Это открывает двери к миру математики и позволяет в полной мере осознавать и ценить ее значимость и важность в нашей жизни.

Значимость понятий

• Описание и классификация: Понятия позволяют нам описывать математические объекты и выделять их основные свойства. Например, понятие «треугольник» описывает геометрическую фигуру, у которой три стороны и три угла.
• Связь и отношения: Понятия помогают нам устанавливать связи и отношения между математическими объектами. Например, понятие «функция» описывает отображение между двумя множествами, где каждому элементу первого множества соответствует единственный элемент второго множества.
• Обобщение и абстракция: Понятия позволяют нам обобщать и абстрагироваться от конкретных примеров и случаев. Например, понятие «вектор» обобщает понятие направленного отрезка, позволяя нам рассматривать его в более абстрактном и общем смысле.
• Разделение и систематизация: Понятия помогают нам разделять и систематизировать математические объекты и их свойства. Например, понятия «четное число» и «нечетное число» разделяют все целые числа на две непересекающиеся категории.
• Установление правил и операций: Понятия позволяют нам устанавливать правила и операции для работы с математическими объектами. Например, понятие «матрица» позволяет нам определить операции сложения и умножения матриц, а также правила их выполнения.

Таким образом, понятия играют важную роль в математике, помогая нам описывать, классифицировать, устанавливать связи и отношения, абстрагироваться от конкретных примеров, разделять и систематизировать математические объекты, а также устанавливать правила и операции для работы с ними.

Видео по теме:

Чем отличается математический термин от понятия?

Математический термин — это специальное слово или выражение, которое используется в математике для обозначения определенного понятия или операции. Он является частью строго определенной системы символов и правил. Понятие, с другой стороны, более широкое и может иметь различные значения и интерпретации в разных контекстах. В математике, понятие может быть использовано для описания более общих и абстрактных идей.

Какие примеры математических терминов?

Примеры математических терминов включают в себя такие понятия, как «функция», «матрица», «дифференциал», «интеграл» и «гипотеза». Эти термины имеют строго определенные значения и используются для обозначения определенных математических концепций.

Какие примеры понятий в математике?

Примеры понятий в математике включают в себя такие идеи, как «число», «множество», «отношение», «фигура» и «пространство». Эти понятия имеют более широкие значения и могут быть интерпретированы по-разному в разных областях математики.

Можно ли использовать математические термины вне математического контекста?

Да, математические термины могут быть использованы вне математического контекста, но их значения и интерпретации могут отличаться. Например, термин «функция» может использоваться в физике или информатике для обозначения отношения или процесса, а не только в математическом смысле.

Какие примеры понятий могут иметь и математическое и не математическое значение?

Примеры понятий, которые могут иметь и математическое, и не математическое значение, включают в себя такие термины, как «сложение», «производная», «множество» и «теория». В математике эти термины имеют строго определенные значения, но они также могут быть использованы в других областях с более широкими или аналогичными значениями.