Что такое число p в математике

Число p (пи) — это математическая константа, которая представляет собой отношение длины окружности к ее диаметру. P является иррациональным числом и приближенно равно 3,14159. Оно широко используется в различных областях математики, физики и инженерии для вычислений, моделирования и построения графиков. Пи также является основой для многих формул и связей в геометрии, тригонометрии и анализе.

Число π (пи) является одним из самых важных и загадочных чисел в математике. Оно известно уже несколько тысячелетий и продолжает удивлять ученых своими свойствами и применениями. Пи является математической константой, которая выражает отношение длины окружности к ее диаметру.

Значение числа π приближенно равно 3,14159, однако его десятичное представление не имеет точного конца и бесконечно длинное. Из-за этого пи является иррациональным числом и не может быть выражено конечной десятичной дробью. Это число было изучено множеством математиков, начиная с древности, и оно встречается во многих областях науки и техники.

Пи имеет множество свойств, которые делают его уникальным и полезным. Например, оно является трансцендентным числом, что означает, что оно не является алгебраическим числом и не может быть решением какого-либо алгебраического уравнения с конечным количеством операций. Это свойство делает пи одним из немногих чисел, которые нельзя выразить аналитически.

Число π имеет огромное практическое значение в различных областях науки и техники. Оно используется в геометрии для вычисления площади и объема кругов, сфер и других геометрических фигур. Также пи применяется в физике, инженерии, статистике, компьютерной графике и других дисциплинах. Благодаря своей уникальности и универсальности, число π остается одной из важнейших констант в математике и науке в целом.

Определение числа p

Число p определяется как отношение длины окружности к ее диаметру. Оно является постоянной величиной и используется в различных областях математики, физики и инженерии.

Значение числа p можно получить с помощью различных методов, включая геометрические, алгебраические и численные подходы. Наиболее распространенным методом вычисления числа p является использование ряда Лейбница или ряда Нилаканта.

Число p имеет множество интересных свойств и является ключевым элементом в различных формулах и уравнениях. Оно используется для вычисления площади круга, объема и площади сферы, а также в других геометрических и тригонометрических формулах.

Число p является одной из наиболее известных и широко используемых математических констант, и его значение имеет важное значение в научных и инженерных расчетах.

Математические свойства числа π

Число π является иррациональным числом, что означает, что его десятичное представление не может быть точно выражено с помощью конечного числа цифр или периодической последовательности. Однако, оно может быть приближенно записано с любой заданной точностью.

Несмотря на свою иррациональность, число π обладает множеством интересных математических свойств. Некоторые из них включают:

• Бесконечность десятичной дроби: Число π является бесконечной десятичной дробью, то есть его десятичное представление содержит бесконечное количество цифр после запятой без периодической последовательности.
• Трансцендентность: Число π является трансцендентным числом, что означает, что оно не является решением любого уравнения с целыми коэффициентами.
• Симметричность: Число π является симметричным относительно вертикальной оси, что означает, что значения функции sin(x) для углов x и π — x совпадают.
• Бесконечность простых чисел: Число π является бесконечным иррациональным числом, что означает, что его десятичное представление не содержит периодической последовательности цифр и бесконечно продолжается без повторений.

Математические свойства числа π имеют широкое применение в различных областях науки и техники, включая геометрию, физику, статистику, теорию вероятности и многие другие.

Расчет числа p

Несмотря на то, что число p является бесконечной десятичной дробью, оно широко используется в различных областях науки, техники и естественных наук.

Существует несколько способов вычисления числа p. Один из наиболее простых способов — метод Монте-Карло. Он основан на генерации случайных точек внутри квадрата со стороной, равной радиусу окружности. Затем подсчитывается количество точек, попавших внутрь окружности. При большом количестве точек отношение числа точек, попавших внутрь окружности, к общему количеству точек будет приближаться к значению числа p.

Другой способ вычисления числа p — формула Лейбница. Она основана на аппроксимации ряда арктангенсами:

pi/4 = 1 — 1/3 + 1/5 — 1/7 + 1/9 — …

Однако, существует еще множество других методов и алгоритмов для расчета числа p с заданной точностью. Различные области науки и техники требуют разных методов вычисления числа p.

Число p в геометрии

В геометрии, число p используется для решения различных задач, связанных с окружностями и кругами. Для окружности, пи является отношением длины окружности к ее диаметру и обозначается символом π.

Одно из важных свойств числа p заключается в том, что оно является постоянным для всех окружностей, независимо от их радиуса или диаметра. Это позволяет использовать его для вычисления различных параметров окружности, таких как площадь, длина дуги, радиус и диаметр.

Также число p встречается в формулах и выражениях, связанных с геометрией. Например, площадь круга вычисляется по формуле S = πr^2, где S — площадь, π — число p, r — радиус окружности.

Необходимо отметить, что число p имеет множество десятичных знаков и не может быть точно представлено в виде конечной десятичной дроби. Поэтому при решении геометрических задач, обычно используют приближенное значение числа p.

Геометрическая фигураФормула

Окружность	Длина окружности: C = 2πr
	Площадь круга: S = πr^2
	Длина дуги: L = αr
Сфера	Площадь поверхности: S = 4πr^2
	Объем: V = (4/3)πr^3
Цилиндр	Площадь боковой поверхности: Sб = 2πrh
	Площадь полной поверхности: Sп = 2πr(r + h)
	Объем: V = πr^2h

Таким образом, число p является важной константой в геометрии и находит широкое применение при решении задач, связанных с окружностями и другими геометрическими фигурами.

Применение числа p в физике

Одно из основных применений числа p в физике — вычисление площади и объема различных геометрических фигур. Например, при расчете площади круга или шара используется формула S = p * r^2, где r — радиус фигуры. Аналогично, для вычисления объема шара используется формула V = (4/3) * p * r^3.

Кроме того, число p используется для определения периодических величин, связанных с колебаниями и волнами. Например, при расчете периода колебаний математического маятника или гармонического осциллятора, используется формула T = 2p * sqrt(l/g), где l — длина маятника, а g — ускорение свободного падения.

Также число p применяется в физике для определения различных физических констант и связанных с ними формул. Например, в формуле для вычисления электрического сопротивления в цепи, сопротивление обозначается символом R = p * (l/A), где l — длина провода, а A — площадь его поперечного сечения.

В заключение, число p играет важную роль в физике, позволяя решать различные задачи и определять физические величины. Его применение распространено в различных областях физики, начиная от геометрии и механики, и заканчивая электродинамикой и оптикой.

Число p в статистике и вероятности

Число p, известное также как математическая константа пи, имеет важное значение не только в математике, но и в статистике и вероятности. В этих областях оно используется для решения различных задач, связанных с анализом данных и оценкой вероятности событий.

В статистике число p играет ключевую роль в распределении нормального закона. Нормальное распределение, также известное как гауссовское распределение, является одним из самых важных и широко используемых распределений в статистике. Оно описывает множество случайных величин, таких как рост людей, вес, IQ и т.д., и имеет форму колокола. В нормальном распределении число p используется для определения критических значений, интервалов доверия и вероятностей для различных статистических тестов.

Вероятность также тесно связана с числом p. Вероятность является мерой того, насколько вероятно возникновение определенного события. Число p используется для оценки вероятности событий, как в классической, так и в статистической вероятности. В классической вероятности число p используется для определения вероятности выпадения определенного исхода в равновероятной ситуации. В статистической вероятности число p используется для определения степени значимости и различия между наблюдаемыми данными и гипотезой.

Область примененияПример

Статистика	Определение критических значений для статистических тестов
Вероятность	Оценка вероятности выпадения определенного исхода

Таким образом, число p имеет важное значение в статистике и вероятности, и играет роль в определении критических значений, интервалов доверия и вероятностей. Оно помогает анализировать данные, проводить статистические тесты и оценивать вероятность различных событий.

Число p в информатике и программировании

Одним из основных применений числа p в информатике является его использование при работе с геометрическими объектами. В программировании часто возникает необходимость вычислять площади и объемы различных фигур, таких как круги, сферы, цилиндры и другие. Для этих вычислений используется формула, в которой число p присутствует в качестве коэффициента. Также число p используется при вычислении длин окружности и других геометрических характеристик.

Кроме того, число p используется при разработке алгоритмов и программ для вычисления и аппроксимации функций. Например, оно может быть использовано при приближенном вычислении тригонометрических функций или при построении интерполяционных полиномов. Также число p может быть использовано при вычислении интегралов и в других численных методах.

В языках программирования число p обычно представляется с помощью встроенной константы, которая имеет высокую точность и позволяет использовать число p без потери точности при вычислениях. Например, в языке Python число p представлено в виде константы math.pi, а в языке Java — константой Math.PI.

Язык программированияКонстанта числа p

Python	math.pi
Java	Math.PI
C++	M_PI

Использование числа p в информатике и программировании позволяет создавать более точные и эффективные алгоритмы для решения различных задач. Оно является неотъемлемой частью многих программ и инструментов, используемых в различных областях, таких как компьютерная графика, машинное обучение, научные исследования и другие.

Вопрос-ответ:

Что такое число p?

Число p, или пи, это математическая константа, которая равна отношению длины окружности к ее диаметру. Точное значение числа p равно примерно 3,14159.

Зачем нужно число p?

Число p имеет множество применений в математике, физике и инженерных науках. Оно используется для вычисления площади и длины окружности, а также для решения различных задач, связанных с геометрией и тригонометрией.

Какое значение имеет число p?

Точное значение числа p равно примерно 3,14159. Однако оно является иррациональным числом, что означает, что его десятичное представление бесконечно и не повторяется.

Какие свойства имеет число p?

Число p обладает множеством интересных свойств. Например, оно является трансцендентным числом, что означает, что его нельзя представить в виде конечной алгебраической десятичной дроби или корня какого-либо алгебраического уравнения с целыми коэффициентами.

Как применяется число p в геометрии?

Число p используется для вычисления площади окружности и длины окружности. Формулы, в которых используется число p, являются основой для множества геометрических вычислений и анализа. Оно также используется для вычисления объема и площади других геометрических фигур, таких как сферы и эллипсы.

Значимость числа p в научных исследованиях

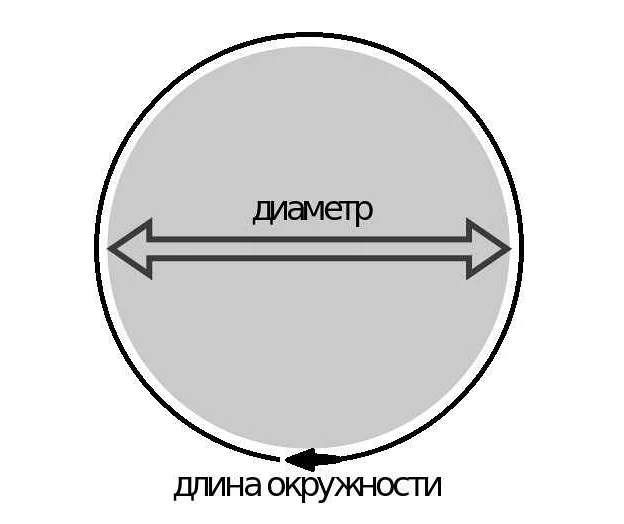
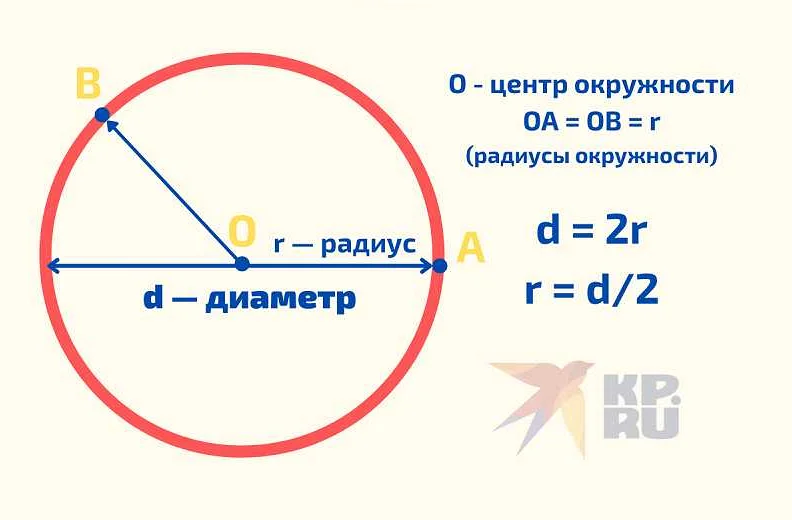
В математике число p определяется как отношение длины окружности к её диаметру и обычно обозначается греческой буквой π. Оно является иррациональным числом, то есть не может быть представлено в виде десятичной дроби или обыкновенной дроби. Приближенное значение числа p равно 3,14159.

Значимость числа p проявляется в различных областях науки. В физике оно используется для расчетов, связанных с окружностями и шаровыми телами. В инженерии и технике оно применяется при проектировании круглых конструкций, например, колес или трубопроводов.

Одна из самых известных формул, связанных с числом p, это формула площади окружности: S = πr^2, где S — площадь окружности, π — число p, r — радиус окружности. Эта формула широко используется в геометрии, физике, инженерии и других науках.

Число p также играет важную роль в статистике и вероятностной теории. Оно используется для расчета вероятностей и для построения статистических моделей. Например, в нормальном распределении — одном из основных распределений в статистике, значение числа p используется для определения границ доверительных интервалов.

Значимость числа p не ограничивается только научными исследованиями. Оно также имеет культурное значение и широко используется в искусстве, музыке и литературе. Например, в числе π имеется бесконечное количество десятичных знаков, и некоторые люди пытаются запомнить как можно больше цифр числа p, что становится своего рода чемпионатом и вызывает интерес у широкой публики.

Таким образом, число p играет важную роль в научных исследованиях, имеет множество применений в различных областях знаний и обладает как математической, так и культурной значимостью.

Видео по теме: