Чему должен научиться ребенок в математике к концу 3 класса: основные знания и умения

Узнайте, какие математические навыки должен усвоить ребенок после третьего класса: от действий с дробями до геометрических фигур. Подготовьте своего ребенка к тому, чтобы успешно продолжать обучение в старших классах и сдавать экзамены на высокие баллы.

Математика – это один из базовых предметов в школьной программе, который оказывает влияние на дальнейшее образование и карьеру. Хорошее понимание математики может стать основой для достижения успеха в таких областях, как наука, технология, инженерия и экономика.

После 3 класса ребенок уже должен знать основные математические понятия и уметь решать простейшие задачи. В этой статье мы рассмотрим основы математики, которые помогут вашему ребенку успешно справляться со сложными математическими задачами в дальнейшем.

Математика может показаться сложным предметом, но понимание основных концепций поможет упростить процесс. Ребенок должен уметь не только решать задачи, но и осознавать, какие математические понятия используются для их решения. Это поможет ему лучше понимать математические принципы и готовиться к более сложным темам в будущем.

Основы математики для дальнейшего образования: что должен уметь ребенок после 3 класса

Математика – это один из важнейших предметов в школьной программе, и после 3 класса ребенок должен иметь некоторые знания и умения, чтобы успешно продолжать обучение этому предмету. Он должен знать основные математические понятия, уметь считать, решать простые задачи, а также строить простые графики и диаграммы.

Важно, чтобы ребенок постоянно практиковался в математике, решая простые упражнения и задачи – именно практика помогает укрепить знания и развить навыки. Кроме того, нужно научить ребенка мыслить математически, понимать логические конструкции и уметь применять их на практике.

После 3 класса ребенок должен уметь:

• складывать, вычитать, умножать и делить числа, простые дроби и десятичные дроби;
• читать числовые выражения и решать простые уравнения;
• анализировать данные и строить графики, диаграммы, таблицы;
• решать простые задачи на нахождение неизвестного числа;
• знать и применять основные математические понятия, такие как: числа, операции, фракции, дроби, проценты, геометрические фигуры, площадь и объем;
• мыслить логически и применять логические принципы в решении задач;
• чтение, записывание и анализ информации из графиков, таблиц и диаграмм.

Освоив эти основы, ребенок будет готов к продолжению обучения математике, постепенно углубляя свои знания и навыки на следующих этапах обучения. Важно помнить, что практика и постоянное развитие математического мышления – это залог успешного овладения этим важным предметом.

Арифметика как основа математики

Арифметика — это одна из основ математики, которую нужно усвоить ребенку уже в начальной школе. Эта область математики занимается изучением основных арифметических операций — сложения, вычитания, умножения и деления.

Важно помнить, что необходимо хорошо понимать базовые понятия арифметики, чтобы можно было успешно изучать более сложные темы в математике. Например, решение уравнений, работы с дробями и процентами требует понимание основных арифметических операций.

В начальной школе ребенок изучает табличное сложение и вычитание, а также таблицу умножения и деления. Так же необходимо уметь решать задачи, которые требуют применения этих операций.

Для успешного обучения арифметике необходимо тренироваться, решая задания разной сложности. Родители могут помочь своему ребенку, предоставляя задания и контролируя правильность их решения.

Таким образом, арифметика является непременным компонентом математического образования в начальной школе и понимание ее основных понятий и операций является необходимым условием для успешного дальнейшего обучения математике.

Понимание дробей и десятичных дробей

Понимание дробей и десятичных дробей является одним из ключевых элементов математического образования для учеников начальной школы. Ребенок должен уметь считать дроби, сравнивать их, и решать задачи, которые требуют знания дробей.

Когда ученик понимает, что дробь представляет собой часть целого числа, он может использовать эту информацию для решения задач. Например, если дробь 1/4 представляет 1 четверть, то 2/4 соответствует 2 четвертям или половине.

После того, как ребенок овладеет пониманием дробей, он должен научиться переводить дроби в десятичные дроби и наоборот. Для этого дети должны знать, что десятичная дробь представляет собой дробь со знаменателем 10. Например, 0,7 — это то же самое, что и 7/10.

Решение задач, связанных с дробями и десятичными дробями, является важным элементом подготовки ученика к более сложным математическим концепциям. Обучение этим навыкам должно основываться на практических примерах, чтобы ученик мог применять их на практике.

1. Ученик должен уметь считать дроби и сравнивать их.
2. Ученик должен уметь переводить дроби в десятичные дроби и наоборот.
3. Решение задач, связанных с дробями и десятичными дробями, является важным элементом подготовки ученика к более сложным математическим концепциям.

Работа с геометрическими фигурами и линиями

После 3 класса ребенок должен уметь работать с различными геометрическими фигурами и линиями. Для начала, он должен уметь различать разные формы геометрических фигур и называть их по имени. Кроме того, ребенок должен уметь измерять углы и длины линий.

Одним из ключевых навыков является работа с прямыми, параллельными и перпендикулярными линиями. Ребенок должен знать, что перпендикулярные линии пересекаются под прямым углом, а параллельные никогда не пересекаются. Также ребенок должен уметь рисовать прямые, параллельные и перпендикулярные линии.

Другим важным навыком является работа с разными видами треугольников. Ребенок должен уметь определить, является ли треугольник прямоугольным или нет, знать, что сумма углов в треугольнике равна 180 градусам, и уметь определять высоту треугольника. Также ребенок должен уметь вычислять площадь треугольника.

Кроме того, ребенок должен знать, как работать с окружностями и измерять их радиусы, диаметры и окружности. Он также должен понимать, что площадь круга можно вычислить по формуле Пи умножить на квадрат радиуса.

В целом, важно, чтобы ребенок после 3 класса знал основные геометрические фигуры и линии, умел измерять углы и линии, работать с кругами и треугольниками, и понимал основные принципы геометрии, которые необходимы для дальнейшего обучения.

Измерения и единицы измерения. Решение задач на перевод единиц

Измерения и единицы измерения – важный раздел математики, который помогает измерять различные физические величины. К данному разделу относятся измерения времени, длины, массы, объема, площади, скорости и многие другие.

Каждая физическая величина имеет свою единицу измерения. Например, для измерения длины используются метры (м), для измерения массы – килограммы (кг), для измерения времени – секунды (с).

Решение задач на перевод единиц включает в себя перевод из одной единицы измерения в другую. Для выполнения задач необходимо знать коэффициенты перевода.

К примеру, для перевода метров в километры необходимо разделить количество метров на 1000, а для перевода километров в метры – умножить количество километров на 1000.

• 1 м = 0,001 км
• 1 км = 1000 м

Кроме того, необходимо учитывать точность измерения и округление чисел.

Работа с измерениями и единицами измерения сложна и требует внимания и точности. Однако, эти знания являются фундаментом для дальнейшего обучения в различных областях – от физики до экономики.

Таблица умножения и деление в столбик

Одним из главных навыков, которые должен усвоить ребенок после 3 класса по математике, является умение быстро и точно умножать и делить. Один из эффективных способов закрепления этих действий — таблица умножения и деления в столбик. Это простой и удобный метод, который можно применять в повседневной жизни и даже на экзаменах.

Таблица умножения и деления в столбик представляет собой таблицу, в которой первый фактор располагается по вертикали, а второй — по горизонтали. В пересечении соответствующих значений получается результат операции. Благодаря использованию этой таблицы, ребенок на примерах может быстро находить ответы и закрепить навыки умножения и деления.

Для закрепления навыков рекомендуется проводить несколько уроков, на которых ребенок будет решать примеры, используя таблицу умножения и деления в столбик. При этом можно использовать как обычные, так и сложные примеры.

Использование таблицы умножения и деления в столбик — это простой и эффективный способ укрепления навыков математики. Малыш здесь научится находить решения даже для сложных примеров всего за несколько шагов. Этот метод необходим для дальнейшего образования, а также для обычной жизни, поэтому необходимо усвоить его как можно раньше.

Пропорции и проценты

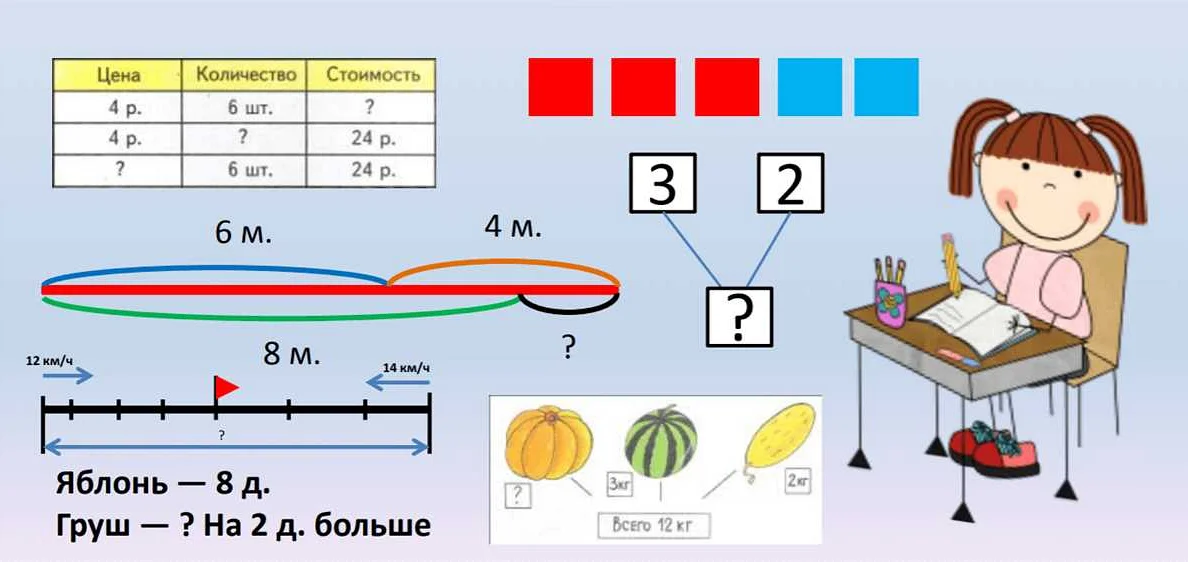
Важным математическим навыком, которым должен обладать ребенок после 3 класса, являются пропорции и проценты. Пропорции используются для сравнения двух или более величин и нахождения неизвестного значения. Знакомым примером пропорции является правило трех: если 1 унция сахара стоит $0.50, то 2 унции будут стоить $1.00 и т.д. Пропорции широко используются в экономике, науке и технике.

Проценты также имеют важное значение в нашей жизни. Они используются для определения доли числа или величины в отношении к 100. Проценты могут использоваться в различных ситуациях, таких как налоги, скидки, процентные ставки по кредитам и вкладам. Ребенок должен уметь считать проценты и решать задачи, связанные с этой темой.

• Для решения задач с пропорциями и процентами нужно знать основные формулы и правила работы с ними.
• Ребенок должен уметь переводить дроби в проценты и наоборот, а также считать конечную величину, если известен процент и исходная величина.
• Необходимо уметь работать с табличными данными, особенно с таблицами процентных ставок, скидок или налоговых ставок.

Понимание пропорций и процентов является важным предварительным условием для изучения более сложных тем, таких как алгебра, геометрия и статистика. Для развития навыков работы с пропорциями и процентами полезно проводить много практических задач и игр, которые бы помогли закрепить пройденный материал и сделать обучение более интересным.

Математический ряд и последовательность

Математический ряд — это сумма бесконечного числа членов, расположенных в определенном порядке. Каждый член ряда называется слагаемым. Математический ряд может быть сходящимся или расходящимся. Сходящийся ряд имеет конечную сумму, а расходящийся ряд — нет.

Последовательность — это совокупность чисел, расположенных в определенном порядке. Каждый элемент последовательности называется членом. Последовательности могут быть возрастающими, убывающими, стационарными или не монотонными. Важной особенностью последовательности является ее предел, который может быть конечным или бесконечным.

Понимание математических рядов и последовательностей является основой для изучения более сложных математических концепций, включая интегралы и дифференциальное исчисление. Разбираться в этих темах без хорошего понимания рядов и последовательностей может быть трудно.

Студенты после 3 класса могут изучать простейшие формулы и последовательности и осознавать, насколько важен определенный порядок для благоприятного исхода. Они могут учиться проводить простейшие математические операции, сравнивать, упорядочивать и анализировать числа и последовательности.

Решение уравнений и неравенств

Ребенок после 3 класса должен уметь решать простейшие уравнения и неравенства. Для решения уравнений и неравенств необходимо знание основ алгебры, таких как операции с числами, приоритет операций и свойства операций.

Для решения уравнений необходимо найти значение переменной, при котором уравнение выполняется. Решение уравнения может быть одним, несколькими или не существовать вовсе. Одним из методов решения уравнений является перенос всех членов уравнения в левую часть и сокращение подобных членов, чтобы осталась только одна переменная. Затем необходимо применить обратную операцию для нахождения значения переменной.

Неравенства могут также содержать переменную и знаки сравнения, такие как «» и «≤». Решение неравенства заключается в определении всех значений переменной, для которых неравенство выполняется. Для этого необходимо учитывать знак сравнения и выполнять операции, чтобы выразить переменную.

Важно понимать, что при выполнении операций с уравнениями и неравенствами необходимо учитывать свойства операций, приоритет операций и правила преобразования выражений. Умение решать уравнения и неравенства является фундаментальным для дальнейшего изучения математики.

Графики и функции

График – это геометрическое изображение зависимости одной величины от другой. Например, график функции y = f(x) – это геометрическое изображение зависимости значения функции y от значения аргумента x.

Для нахождения графика функции можно построить таблицу значений и отметить точки на координатной плоскости. Однако, более удобным способом является построение графика по формуле функции. Для этого необходимо выбрать некоторое количество различных значений аргумента, подставить их в формулу функции и найти соответствующие значения функции. Затем эти точки можно отметить на координатной плоскости и провести через них гладкую кривую, являющуюся графиком функции.

Функция – это математический объект, который каждому элементу из одного множества (аргументу) ставит в соответствие один элемент из другого множества (значение). Например, функция y = f(x) может ставить в соответствие каждому значению x его квадрат.

Знание графиков и функций необходимо для дальнейшего изучения математики, в частности – алгебры, геометрии. С помощью графиков и функций удобно и наглядно представлять зависимости между различными величинами, а также решать уравнения и неравенства.

Кроме того, знание графиков и функций полезно в повседневной жизни, например, для расчета стоимости проезда по автомагистрали в зависимости от расстояния, или для построения графиков доходности вкладов в банках.

Примеры функцийГрафик функции

y = x^2
y = sin(x)

Видео по теме:

Вопрос-ответ:

Какую математику должен знать ребенок после 3 класса?

Ребенок после 3 класса должен уметь решать задачи на сложение, вычитание, умножение и деление, знать таблицу умножения, уметь работать с дробями, знать основные геометрические фигуры и уметь измерять длины, площади и объемы.

Какие математические навыки помогут ребенку в дальнейшем образовании?

Знание основ математики после 3 класса поможет ребенку успешно продолжать учебу в школе и более сложных областях математики, таких как алгебра, геометрия и тригонометрия. Кроме того, математические навыки помогут ребенку развивать логическое мышление и выработать навыки решения проблем и анализа данных.

Какие математические темы наиболее важны для подготовки к дальнейшему образованию?

Наиболее важные математические темы для подготовки к дальнейшему образованию включают в себя арифметику (основные операции, дроби, десятичные дроби и проценты), алгебру (алгебраические выражения, уравнения и неравенства), геометрию (геометрические фигуры, площадь, объем и углы) и статистику (построение графиков и анализ данных).

Какие математические навыки наилучшим образом развивать после 3 класса?

После 3 класса рекомендуется развивать навыки решения задач и анализа данных, таких как построение таблиц и графиков. Также важно правильно учить таблицу умножения и усваивать понятия дробей и процентов, а также практиковаться в работе со счетными и несчетными множествами.

На что стоит обратить внимание родителям, если ребенок испытывает трудности в математике?

Родители могут обратить внимание на то, как ребенок учит математику и какие методы ему используются в школе. Если ребенок испытывает трудности в понимании материала, то родители могут попробовать помочь ему разобраться с задачами, использовать дополнительные материалы или найти репетитора. Также стоит проверить, что ребенок понимает основные понятия и термины, связанные с математикой.

Какие математические игры и задания помогут ребенку развиваться после 3 класса?

После 3 класса ребенку становятся доступными игры и задания, связанные с логикой, алгеброй и геометрией. Например, можно предложить ребенку решать головоломки и задачи на логику, играть в шахматы, судоку или кроссворды. Также можно предложить ребенку построить модели из конструкторов или на бумаге, используя знания о геометрии.

Как важно обучение математике после 3 класса для дальнейшей карьеры ребенка?

Обучение математике после 3 класса играет важную роль в дальнейшей карьере ребенка, особенно если он выберет научную или инженерную специальность. Знания в области алгебры, геометрии и тригонометрии могут помочь ребенку решать сложные задачи и участвовать в проектах, связанных с научными и инженерными отраслями.

Векторы и координаты

Вектор — это математический объект, который может быть полностью определен направлением и длиной. Вектор обычно обозначается стрелкой, которая указывает на ту сторону, в которую направлен вектор.

Координатная плоскость — это способ задания точки на плоскости при помощи двух чисел — координат. Первое число является координатой по оси X, а второе — по оси Y. Таким образом, каждая точка на плоскости имеет свои уникальные координаты.

Для задания вектора на плоскости, его можно задать при помощи координат его начала (начальная точка вектора) и конца (конечная точка вектора). Также можно использовать нотацию векторов, задавая направление и длину вектора в специальном виде.

• Сложение векторов — это операция, при которой два или более вектора складываются вместе, чтобы получить новый вектор. При сложении векторов сумма длин векторов будет проекцией результирующего вектора на ось, соответствующую данной проекции.
• Умножение вектора на число — это операция, при которой вектор умножается на константу, чтобы получить новый вектор. Результатом этой операции является вектор, имеющий ту же направленность, что и исходный вектор, но с измененной длиной.

Векторы и координаты — это важные основы математики, которые дети учатся изучать после 3 класса. Понимание этих концепций абсолютно необходимо для понимания более сложных математических концепций, таких как геометрия и алгебра.

Логические и математические задачи для развития умственных способностей

Развитие умственных способностей является важным элементом в обучении математике. Решение математических задач требует от ребенка логического мышления, умения анализировать и строить последовательности действий. Помимо уроков математики, домашние задания и дополнительные занятия с репетитором, можно проводить дополнительные занятия в форме различных игр, головоломок, головокружительных задач и т.д.

Например, одной из игр на развитие умственных способностей может стать шахматы. Игра требует от игроков умения анализировать положение фигур на доске, планировать ходы и прогнозировать возможные ходы противника. Также можно проводить занятия по логике и грамматике, которые требуют от ребенка умения анализировать и воспринимать последовательности информации.

Также существует множество математических игр и задач, которые помогут тренировать мозг ребенка. Например, игра «Судоку» требует от игрока умения работать с числами, анализировать положение цифр на поле и строить правильные комбинации. Также можно проводить игры на ассоциации, математические головоломки, геометрические конструкции и т.д.

• Игры на ассоциации помогут ребенку развивать лексический запас, укреплять память и логическое мышление.
• Математические головоломки и задачи помогут тренировать умение анализировать и делать логические выводы.
• Геометрические конструкции помогут ребенку научиться анализировать пространственные объекты и строить логические цепочки.

Таким образом, проведение дополнительных занятий и игр поможет ребенку развивать умственные способности и повышать качество обучения математике.