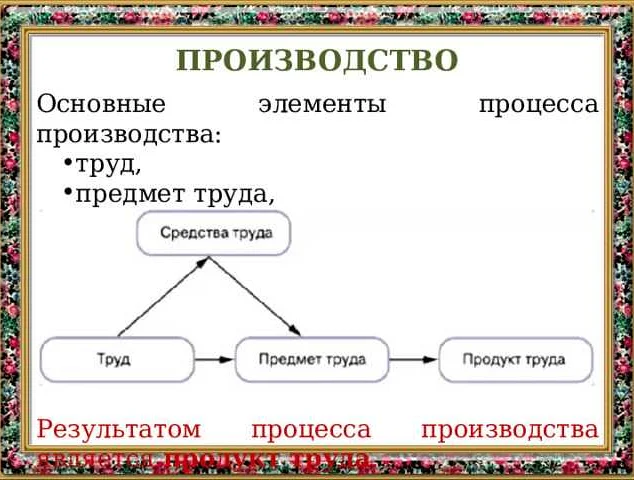
Подумайте что является продуктом труда для математика

Продуктом труда для математика являются новые теоремы и методы, которые помогают решать сложные задачи и расширяют наши знания о мире чисел и формул. Узнайте, как математики создают и открывают новые математические концепции и применения.

Математика – это одна из старейших и наиболее сложных наук, которая изучает структуру, свойства и взаимосвязи чисел, пространств, форм и понятий. Она играет фундаментальную роль в различных областях науки, техники, экономики и социальных наук. Однако, часто задаешься вопросом: каков же продукт труда математика?

Для математика главным продуктом его труда является глубокий анализ. Он исследует и разбирает математические объекты и явления, раскрывая их внутреннюю структуру и закономерности. Математик анализирует уже известные концепции и теории, выявляя их проблемы и ограничения, а также ищет новые пути и подходы для их развития и усовершенствования.

Глубокий анализ математических концепций позволяет математикам создавать новые теории, методы и модели, которые находят свое применение как в самой математике, так и в других областях науки и техники. Он способствует развитию новых концепций и открытию новых связей между различными математическими областями.

Кроме того, развитие новых концепций является также важным продуктом труда математика. Он стремится создать новые математические модели и концепции, которые помогают решать сложные проблемы и задачи в различных областях. Такие новые концепции могут иметь далеко идущие последствия и применение в практике, стимулируя развитие науки и технологий.

В целом, продукт труда математика – это не только новые теории и модели, но и развитие и усовершенствование уже существующих концепций. Это стремление к пониманию и раскрытию фундаментальных законов исследуемых объектов, а также создание новых инструментов и методов для их изучения и применения.

Что является результатом работы математика: изучение, анализ и разработка новых идей

Основной инструмент работы математика – это анализ. Математик, исследуя различные математические структуры и объекты, проводит глубокий анализ и пытается выявить их особенности и свойства. Он изучает законы и правила, которыми руководствуются эти структуры, и стремится выявить новые закономерности и теоретические результаты.

Еще одним важным результатом работы математика является разработка новых идей. Математик, работая с различными математическими объектами, старается прийти к новым предложениям, теориям и моделям. Он стремится проложить путь для развития математики и создать новые инструменты для решения проблем и задач.

Итак, результатом работы математика является глубокий анализ и изучение математических структур, а также разработка новых идей и концепций. Математики играют важную роль в развитии науки и технологий, их открытия и результаты имеют широкие практические применения в различных областях нашей жизни.

Развитие математических концепций и теорий

Развитие математических концепций и теорий основано на систематическом изучении и анализе уже существующих математических знаний. Математик проводит глубокий анализ различных математических структур и объектов, обнаруживает их свойства и закономерности, строит модели и формализует эти закономерности в виде математических теорий и концепций.

Одним из важных аспектов развития математических концепций и теорий является поиск новых подходов и методов исследования. Математик стремится найти новые способы решения задач, разработать новые технологии и методы, которые позволят ему расширить границы уже существующих математических теорий и открыть новые области исследования.

Важным аспектом развития математических концепций и теорий является также обмен знаниями и идеями с другими математиками. Совместные исследования, обсуждение результатов и обмен опытом позволяют математикам взаимно влиять на развитие математической науки и создавать новое знание вместе.

В итоге, развитие математических концепций и теорий позволяет математикам расширять границы математического знания и понимания, создавать новые инструменты и методы для решения сложных задач, а также открывать новые области исследования. Это делает математику неотъемлемой частью развития науки и технологий в целом.

Глубокий анализ математических объектов и структур

Математик проводит анализ различных математических объектов, таких как числа, функции, графы, алгебраические структуры и другие. В процессе анализа математик исследует их свойства, взаимосвязи и взаимодействия, а также устанавливает закономерности и правила, которыми они руководствуются.

Глубокий анализ математических объектов и структур позволяет математику выявить общие закономерности и принципы, которые лежат в основе различных математических концепций. Это важно для развития новых идей и теорий в математике.

В процессе анализа математик использует различные методы и техники, такие как доказательства, логика, алгоритмы и моделирование. Он также активно использует компьютерные технологии и программы для проведения анализа и исследования математических объектов.

Глубокий анализ математических объектов и структур помогает математику не только углубить свои знания и понимание в области математики, но и создать новые математические концепции и теории. Это открытия и результаты анализа послужат основой для дальнейшего развития математики и ее применения в других науках и областях.

Таким образом, глубокий анализ математических объектов и структур играет важную роль в работе математика, позволяя ему расширить границы знаний и создать новые концепции и идеи.

Решение сложных математических проблем

Математики занимаются решением сложных математических проблем, которые могут иметь важное значение для различных областей науки и технологий. Они разрабатывают новые методы и теории, анализируют существующие концепции и создают новые, позволяющие эффективно решать сложные математические проблемы.

Одной из основных целей математиков является разработка алгоритмов и моделей для решения сложных задач. Они исследуют математические структуры и применяют их для анализа и моделирования реальных систем. Кроме того, математики также разрабатывают новые методы для решения оптимизационных задач, которые часто встречаются в научных и технических приложениях.

Решение сложных математических проблем требует глубокого анализа и владения различными математическими концепциями. Математики занимаются исследованием и развитием новых теорий, позволяющих решать сложные задачи, а также разработкой новых методов вычислений и алгоритмов.

Благодаря работе математиков ученые и инженеры получают возможность разрабатывать новые технологии и решать сложные проблемы в различных областях, таких как физика, экономика, биология и компьютерные науки. Результаты исследований математиков могут применяться в различных приложениях, от криптографии и сжатия данных до оптимизации производственных процессов и прогнозирования рыночных трендов.

Таким образом, решение сложных математических проблем является продуктом труда математиков и имеет важное значение для развития науки и технологий. Оно позволяет находить новые решения для сложных задач и применять их в практических приложениях, что способствует развитию общества и прогрессу человечества.

Создание новых методов и алгоритмов

Для создания новых методов и алгоритмов математики производят глубокий анализ существующих моделей и подходов. Они исследуют различные математические структуры, проводят эксперименты и тестируют различные варианты. В результате этой работы они приходят к новым идеям и концепциям, которые могут быть применены для решения сложных задач.

Создание новых методов и алгоритмов требует не только глубоких знаний и понимания математических концепций, но и творческого подхода. Математики часто используют интуицию, логическое мышление и абстрактное мышление для создания новых подходов и решений.

Новые методы и алгоритмы, созданные математиками, могут применяться в различных областях, таких как физика, экономика, компьютерная наука и другие. Они могут помочь в решении сложных задач, оптимизации процессов и разработке новых технологий.

Таким образом, создание новых методов и алгоритмов является важным продуктом труда математика. Это позволяет им не только развивать новые концепции, но и вносить вклад в различные области науки и технологий.

Исследование и развитие математической логики

Математическая логика позволяет проводить глубокий анализ математических концепций и доказательств, а также разрабатывать новые методы исследования в различных областях математики. Она служит основой для формализации математических теорий и построения формальных систем, которые позволяют с помощью точных математических методов анализировать и решать сложные задачи.

Исследование математической логики позволяет выявлять и анализировать закономерности и связи между математическими объектами, а также разрабатывать новые концепции и теории. Это позволяет углубить понимание математических структур и процессов, а также создавать новые методы и приемы решения математических задач.

Развитие математической логики имеет огромное значение не только для математики, но и для других наук, таких как информатика, физика, философия и теоретическая биология. Использование математической логики позволяет формализовать и анализировать сложные концепции и процессы в этих науках, а также обеспечить точность и строгость математических рассуждений.

Таким образом, исследование и развитие математической логики являются важным продуктом труда для математика. Они позволяют не только расширить границы математических знаний, но и создать новые методы и подходы, которые способствуют развитию науки и прогрессу в обществе.

Применение математики в других науках и областях

В физике математика используется для описания и предсказания физических явлений. Например, в классической механике математические методы используются для моделирования движения тел и решения уравнений движения. В квантовой физике математика помогает описывать вероятности и взаимодействие элементарных частиц.

В химии математика используется для анализа и предсказания свойств и реакций химических соединений. Математические модели позволяют исследовать кинетику реакций, оптимизировать условия синтеза и прогнозировать свойства новых соединений.

В биологии математика применяется для анализа генетических данных, моделирования эволюции организмов, описания биологических систем и прогнозирования их поведения. Например, математические модели позволяют исследовать распространение болезней, взаимодействие видов в экосистемах и динамику популяций.

В экономике математика широко применяется для анализа и оптимизации экономических процессов. Математические модели позволяют исследовать взаимосвязь между производством, потреблением и ценами, прогнозировать поведение рынков и принимать решения в условиях неопределенности.

В компьютерных науках математика играет важную роль в алгоритмах и структурах данных. Математические методы применяются для оптимизации работы компьютерных систем, разработки криптографических алгоритмов и исследования искусственного интеллекта.

Применение математики в других науках и областях позволяет ученым получать новые знания, разрабатывать новые концепции и решать сложные проблемы. Без математического анализа и развития новых математических концепций многие исследования были бы невозможными.

Видео по теме:

Вопрос-ответ:

Для чего математику нужен глубокий анализ?

Глубокий анализ позволяет математику углубить свои знания в определенной области и развить новые концепции, что является ключевым для прогресса в математике. Благодаря глубокому анализу математики могут решать сложные задачи и открывать новые законы и теории.

Какие преимущества дает развитие новых концепций для математика?

Развитие новых концепций позволяет математику проникнуть в глубину изучаемой проблемы и найти новые методы решения сложных задач. Это также способствует развитию общей теории и позволяет математикам создавать новые модели и предсказывать результаты экспериментов.

Как можно применить глубокий анализ и развитие новых концепций в повседневной жизни?

Глубокий анализ и развитие новых концепций могут помочь в решении сложных задач и проблем, как в научной сфере, так и в повседневной жизни. Они позволяют лучше понять причинно-следственные связи, анализировать большие объемы информации и прогнозировать результаты. Например, это может быть полезно при принятии решений в финансовой сфере, в управлении проектами или при разработке новых технологий.

Какие навыки развивает глубокий анализ и развитие новых концепций?

Глубокий анализ и развитие новых концепций развивают аналитическое мышление, способность видеть связи и закономерности, критическое мышление, творческий подход к решению задач, а также умение работать с большими объемами информации и прогнозировать результаты. Также это способствует развитию технических навыков и умениям применять полученные знания на практике.

Какие риски связаны с глубоким анализом и развитием новых концепций?

Глубокий анализ и развитие новых концепций могут быть связаны с риском зацикливания на одной проблеме или идеи, что может отнимать много времени и энергии. Также возможны риски неправильного анализа или разработки неправильных концепций, что может привести к неверным выводам и ошибкам. Поэтому важно иметь критическое мышление и проверять полученные результаты.

Развитие математической образовательной системы

Развитие математической образовательной системы направлено на создание эффективных методов преподавания математики, а также на разработку новых концепций и подходов к обучению. Глубокий анализ математических концепций и их развитие позволяют улучшить качество образования и повысить его доступность для всех студентов.

Одной из основных задач развития математической образовательной системы является формирование у студентов навыков решения математических задач и применения полученных знаний на практике. Это позволяет им успешно справляться с сложными задачами в различных сферах деятельности, таких как экономика, физика, информационные технологии и другие.

Важной составляющей развития математической образовательной системы является использование современных информационных технологий в процессе обучения. Это позволяет студентам лучше понимать математические концепции, проводить визуализацию и анализ данных, а также применять компьютерные программы для решения сложных математических задач.

Кроме того, развитие математической образовательной системы способствует формированию у студентов умения работать в команде, проводить исследования и презентовать свои научные результаты. Это развивает их креативность, коммуникативные навыки и способность к самостоятельной работе.

В заключение, развитие математической образовательной системы играет важную роль в формировании качественных знаний и навыков у студентов. Оно способствует развитию науки и технологий, а также обеспечивает студентам возможности для успешной карьеры в различных областях деятельности.

Влияние математических открытий на технологический прогресс

Математика играет важную роль в развитии технологий и влияет на множество отраслей человеческой деятельности. Математические открытия и разработки позволяют улучшать существующие технологии, создавать новые продукты и решать сложные проблемы.

Одной из отраслей, в которой математика имеет наибольшее влияние, является компьютерная технология. Многие алгоритмы и методы, используемые в программировании, основаны на математических концепциях, таких как логика, графы, алгебра и дискретная математика. Благодаря математике были разработаны эффективные алгоритмы сортировки, поиска, шифрования и многие другие, которые являются основой для работы многих компьютерных систем и программ.

Математические модели также широко используются в физике, инженерии и других науках, чтобы описывать и предсказывать различные физические процессы и явления. Например, дифференциальные уравнения, разработанные математиками, позволяют моделировать движение тел, электромагнитные поля, распространение волн и многие другие физические явления. Эти модели являются основой для разработки новых технологий, таких как радио, телевизоры и мобильные устройства.

Математика также играет важную роль в развитии искусственного интеллекта и машинного обучения. Алгоритмы машинного обучения основаны на математических методах статистики, оптимизации и теории вероятностей. Они позволяют компьютерам обрабатывать большие объемы данных, анализировать их и делать прогнозы. Благодаря математике были созданы различные интеллектуальные системы и роботы, которые используются в медицине, транспорте, финансах и других отраслях.

Таким образом, математические открытия имеют огромное значение для технологического прогресса. Они позволяют разрабатывать новые продукты, повышать эффективность существующих технологий и решать сложные задачи, которые ранее казались неразрешимыми. Математики продолжают вносить вклад в развитие технологий и исследование новых концепций, что помогает улучшать нашу жизнь и прогресс человечества в целом.