Что нужно знать для егэ по математике база
Содержимое
- 1 Что нужно знать для егэ по математике база
- 1.1 Тема 1: Алгебра
- 1.2 Основы алгебры: понятия и примеры
- 1.3 Тема 2: Геометрия
- 1.4 Основы геометрии: понятия и примеры
- 1.5 Тема 3: Тригонометрия
- 1.6 Основы тригонометрии: понятия и примеры
- 1.7 Тема 4: Функции
- 1.8 Основы функций: понятия и примеры
- 1.9 Тема 5: Производные и интегралы
- 1.10 Основы производных и интегралов: понятия и примеры
- 1.11 Видео по теме:
В этой статье вы узнаете все необходимое для успешной подготовки к экзамену ЕГЭ по математике базового уровня. Мы расскажем вам о ключевых темах, формате заданий и дадим полезные советы по подготовке. Получите необходимые знания и навыки, чтобы сдать экзамен на высокие баллы!
ЕГЭ по математике является одним из самых важных экзаменов для многих выпускников школы. Этот экзамен проверяет не только знания учеников, но и их способность применять математические методы для решения различных задач. Подготовка к ЕГЭ по математике требует времени и усилий, но с правильным подходом можно достичь хороших результатов.
Основные темы, которые обычно включаются в программу ЕГЭ по математике, включают алгебру, геометрию, математический анализ и теорию вероятности. В алгебре, ученики изучают алгебраические операции, уравнения и неравенства, функции и последовательности. В геометрии, они изучают различные фигуры, теоремы и свойства. В математическом анализе, ученики изучают дифференциальное и интегральное исчисление, а также их применение. В теории вероятности, ученики изучают вероятностные модели и задачи.
Правила подготовки к ЕГЭ по математике база включают регулярное изучение материала, решение задач разной сложности и проведение тренировочных тестов. Важно также понимать основные концепции и методы, а не просто зубрить формулы. Рекомендуется использовать различные учебники и задачники, а также обращаться за помощью к учителям и преподавателям. Также полезно решать задачи из предыдущих экзаменов и использовать онлайн-ресурсы для подготовки к ЕГЭ по математике база.
Подготовка к ЕГЭ по математике требует систематического и упорного подхода. Соответствующая подготовка позволяет ученикам уверенно справляться с задачами экзамена и демонстрировать свои знания и умения. Соответствие программе, глубина знаний и умение применять их в практических задачах являются основными критериями оценки. Стремление к достижению высоких результатов в ЕГЭ по математике база требует усилий и настойчивости, но приводит к положительным результатам и может открыть двери в хорошие учебные заведения и будущие карьерные возможности.
Тема 1: Алгебра
Основные темы, которые следует изучить для успешной подготовки к ЕГЭ по алгебре, включают в себя:
- Арифметические операции – сложение, вычитание, умножение и деление чисел;
- Рациональные числа – понятие о дробях, операции с дробями;
- Степени и корни – определение, свойства и операции со степенями и корнями;
- Линейные уравнения и неравенства – решение уравнений и неравенств с одной переменной;
- Системы уравнений – решение систем линейных уравнений;
- Квадратные уравнения и неравенства – решение квадратных уравнений и неравенств;
- Функции и графики – понятие функции, построение графиков функций;
- Пределы функций – определение и свойства пределов функций.
Знание этих тем позволит справиться с большинством заданий по алгебре на ЕГЭ. Важно понимать основные понятия, уметь применять соответствующие формулы и законы, а также уметь решать практические задачи на основе алгебраических знаний.
Для успешной подготовки к ЕГЭ по алгебре рекомендуется регулярно решать задачи разной сложности, использовать специальные пособия и учебники, а также обращаться за помощью к преподавателям и репетиторам по математике.
Основы алгебры: понятия и примеры
В алгебре ключевыми понятиями являются переменные, константы, термы и уравнения. Переменная — это символ, который представляет неизвестное значение. Константа — это число, которое является известным и не меняется. Терм — это выражение, состоящее из переменных и/или констант, связанных с помощью арифметических операций. Уравнение — это равенство двух термов, содержащее одну или несколько переменных, которое требуется решить.
Примером простого уравнения может служить следующее: x + 5 = 10. В данном уравнении x — переменная, 5 — константа, x + 5 — терм, 10 — также константа. Чтобы решить это уравнение, необходимо найти значение переменной x, при котором равенство будет выполняться.
Для решения уравнений существуют различные методы, такие как метод подстановки, метод равных коэффициентов и метод графического представления. Важно уметь применять эти методы и использовать алгебраические преобразования для приведения уравнений к более простому виду.
Основы алгебры также включают в себя понятия пропорции и проценты. Пропорция — это равенство двух отношений, в котором каждое отношение представляет собой частное двух величин. Процент — это способ представления доли величины относительно целого, которое равно 100%. Умение работать с пропорциями и процентами необходимо для решения задач на практике.
Основы алгебры играют важную роль в ЕГЭ по математике база, поэтому рекомендуется уделить им достаточно времени и внимания при подготовке к экзамену.
Тема 2: Геометрия
Основные темы, связанные с геометрией, включают:
- Планиметрия — изучение плоских геометрических фигур, таких как треугольники, квадраты, прямоугольники и круги. Важным аспектом планиметрии является вычисление площадей и периметров фигур.
- Стереометрия — изучение пространственных геометрических фигур, таких как параллелепипеды, пирамиды, конусы и шары. Здесь важно уметь вычислять объемы и площади поверхностей данных фигур.
- Координатная геометрия — изучение геометрии на плоскости с использованием координат. Это включает в себя работу с графиками функций, нахождение расстояний между точками и определение углов наклона прямых.
- Тригонометрия — изучение связей между сторонами и углами в треугольниках. Здесь важно знать основные тригонометрические функции, такие как синус, косинус и тангенс, а также уметь решать уравнения и неравенства с использованием этих функций.
Для успешной подготовки к ЕГЭ по математике важно уделить достаточное время изучению и практике задач по геометрии. Регулярная тренировка поможет улучшить понимание теории и научиться применять ее на практике. Также полезно ознакомиться с типовыми заданиями, которые могут встретиться на экзамене, и изучить стратегии и подходы к их решению.
Основы геометрии: понятия и примеры
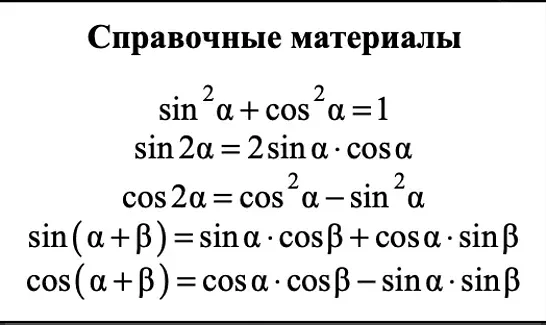
Одним из основных понятий геометрии является понятие точки. Точка – это элементарный объект, не имеющий никаких размеров. Она обозначается заглавной латинской буквой. Две или более точек могут образовывать линию или отрезок.
Линия – это набор бесконечного числа точек, протяженный в одном направлении. Линии могут быть прямыми или кривыми. Прямая – это линия, которая не имеет изгибов или углов. Прямые обозначаются строчными латинскими буквами. Кривая – это линия, которая может иметь изгибы и углы.
Отрезок – это часть прямой, ограниченная двумя точками. Он обозначается двумя точками с чертой над ними.
В геометрии также существуют фигуры, которые образуются при соединении точек и линий. Например, треугольник – это фигура, которая образуется при соединении трех точек, не лежащих на одной прямой. Треугольник имеет три стороны и три угла.
Еще одной важной фигурой в геометрии является круг. Круг – это фигура, которая образуется при соединении всех точек, находящихся на одинаковом расстоянии от центра. Особенностью круга является радиус – расстояние от центра круга до любой его точки.
Знание основных понятий геометрии и умение применять их в решении задач является необходимым для успешной сдачи экзамена по математике ЕГЭ.
Тема 3: Тригонометрия
Основные понятия в тригонометрии:
- Угол – геометрическая фигура, образованная двумя лучами с общим началом.
- Радианная мера угла – величина, определяющая отношение длины дуги к радиусу окружности.
- Тригонометрические функции – функции, описывающие отношения между сторонами и углами в треугольниках.
Основные тригонометрические функции:
- Синус (sin) – отношение противолежащего катета к гипотенузе.
- Косинус (cos) – отношение прилежащего катета к гипотенузе.
- Тангенс (tg) – отношение противолежащего катета к прилежащему катету.
- Котангенс (ctg) – отношение прилежащего катета к противолежащему катету.
Применение тригонометрии:
- Решение треугольников – определение значений сторон и углов треугольника по заданным данным.
- Решение тригонометрических уравнений и неравенств.
- Построение графиков тригонометрических функций.
Правила подготовки к теме «Тригонометрия» на экзамене:
- Ознакомьтесь с основными понятиями и тригонометрическими функциями.
- Изучите формулы и свойства тригонометрических функций.
- Научитесь использовать таблицы и графики тригонометрических функций.
- Решайте задачи на построение графиков, решение уравнений и неравенств с использованием тригонометрии.
- Повторяйте материал и регулярно решайте задачи из заданий на ЕГЭ.
Основы тригонометрии: понятия и примеры
Основными понятиями в тригонометрии являются синус, косинус и тангенс. Синус определяется как отношение противолежащего катета к гипотенузе треугольника. Косинус – это отношение прилежащего катета к гипотенузе. Тангенс – это отношение противолежащего катета к прилежащему катету. Эти понятия обычно обозначаются как sin, cos и tan соответственно.
Для работы с тригонометрическими функциями используются углы в радианах. Радиан – это единица измерения угла, которая соответствует отношению длины дуги окружности к радиусу. Важно помнить, что угол в радианах равен длине дуги, заключенной между двумя радиусами, деленной на радиус окружности.
Примеры использования тригонометрии в различных задачах могут включать определение высоты объекта по углу наблюдения, определение длины недоступной стороны треугольника и вычисление силы, действующей на объект под углом.
Таким образом, знание основных понятий тригонометрии и умение применять их в задачах является важным для успешной подготовки к ЕГЭ по математике. Систематическое изучение тригонометрии и регулярная тренировка помогут студентам уверенно справиться с экзаменационными вопросами и задачами.
Тема 4: Функции

Функции широко используются в математике и других науках для моделирования различных явлений и процессов. Также функции являются важным инструментом при решении задач в экономике, физике, информатике и других областях.
Основные понятия, связанные с функциями, включают:
- Область определения: множество всех значений, для которых функция определена.
- Область значений: множество всех значений, которые функция может принимать.
- График функции: геометрическое представление функции на координатной плоскости.
- Линейная функция: функция, заданная уравнением вида y = kx + b, где k и b — константы.
- Квадратичная функция: функция, заданная уравнением вида y = ax^2 + bx + c, где a, b и c — константы.
- Парабола: график квадратичной функции, имеющий форму дуги.
Для успешного решения задач по функциям необходимо хорошо знать основные свойства функций, уметь строить графики функций и решать уравнения, связанные с функциями. Также полезно знать основные классы функций, такие как линейные и квадратичные функции, и уметь применять их для решения задач.
Основы функций: понятия и примеры
Примером функции может служить функция f(x) = 2x + 3. В данном примере x является аргументом функции, а 2x + 3 — значением функции при данном аргументе. Подставляя различные значения для x, мы можем получить соответствующие значения функции. Например, при x = 1 значение функции будет равно 5 (2 * 1 + 3 = 5), а при x = 2 значение функции будет равно 7 (2 * 2 + 3 = 7).
Функции могут быть представлены в виде графиков. График функции — это изображение точек, которые соответствуют значениям функции при различных значениях аргумента. График функции f(x) = 2x + 3 будет представлен прямой линией, так как это линейная функция.
Основные понятия, связанные с функциями, включают область определения и область значений функции. Область определения — это множество значений, для которых функция определена. Область значений — это множество значений, которые функция может принимать.
Например, для функции f(x) = 2x + 3, область определения — это множество всех действительных чисел, так как функция определена для любого значения x. Область значений — это множество всех действительных чисел, так как функция может принимать любое значение.
Знание основных понятий и примеров функций является важным для успешной подготовки к ЕГЭ по математике. На экзамене вам могут задать задачи, связанные с функциями, и без понимания этих концепций вы можете испытать трудности в их решении.
Тема 5: Производные и интегралы
Производная функции является основным понятием в теории дифференцирования. Она позволяет определить скорость изменения функции в каждой точке ее области определения. Производная функции может быть определена как предел отношения изменения значения функции к изменению ее аргумента при стремлении изменения аргумента к нулю. Производные функций позволяют найти точки экстремума, определить монотонность функции, построить график функции и решить множество задач на оптимизацию.
Интеграл от функции является обратной операцией к дифференцированию. Он позволяет найти площадь под графиком функции, а также вычислить определенный интеграл для нахождения значения определенного интеграла в заданных пределах. Интегралы являются основным инструментом в задачах на вычисление площадей и объемов, а также нахождение средних значений функций.
Подготовка к ЕГЭ по теме «Производные и интегралы» включает в себя изучение основных понятий, формул и методов решения задач, а также выполнение множества практических заданий и их последующую проверку и анализ. Знание и понимание основных свойств производных и интегралов, а также умение применять их в различных системах задач, позволят успешно справиться с этой темой на экзамене.
Основы производных и интегралов: понятия и примеры

Производная функции в точке определяется как предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю. Она показывает скорость изменения функции в данной точке и является мощным инструментом для изучения графиков функций. Производная функции в точке может быть положительной, отрицательной или равной нулю, что указывает на рост, убывание или экстремум функции соответственно.
Интеграл функции от а до b представляет собой площадь между графиком функции и осью абсцисс на отрезке [a, b]. Он является инверсией процесса нахождения производной и позволяет находить площади под графиками сложных функций. Интеграл может быть определенным или неопределенным, в зависимости от наличия или отсутствия пределов интегрирования.
Ниже приведены примеры использования производных и интегралов:
Примеры производныхПримеры интегралов
| Вычисление скорости движения объекта | Вычисление площади под графиком функции |
| Определение точек экстремума функции | Нахождение объема тела с помощью исследования площади поперечного сечения |
| Анализ максимальной и минимальной скорости функции | Нахождение среднего значения функции на отрезке |
Овладение основами производных и интегралов позволяет эффективно решать задачи на ЕГЭ и использовать математический анализ в дальнейшем образовании и профессиональной деятельности.
Видео по теме:
Какие основные темы нужно знать для сдачи ЕГЭ по математике?
Основные темы для сдачи ЕГЭ по математике включают алгебру, геометрию, теорию вероятности и математическую статистику. В алгебре необходимо знать основные операции, линейные и квадратные уравнения, работу с функциями, графики функций и преобразования функций. В геометрии нужно знать основные понятия, такие как точка, прямая, угол, треугольник, окружность, а также уметь решать задачи на построение геометрических фигур. Теория вероятности и математическая статистика включают понятия вероятности, случайной величины, закона распределения, математического ожидания и дисперсии.
Какие основные темы входят в программу ЕГЭ по математике база?
В программу ЕГЭ по математике база входят следующие основные темы: алгебра и начала математического анализа, геометрия и начала теории вероятностей. Каждая из этих тем имеет свои подтемы и конкретные задания, которые необходимо уметь решать для успешной сдачи экзамена.
Какие правила подготовки к ЕГЭ по математике база нужно знать?
Для успешной подготовки к ЕГЭ по математике база нужно учиться систематически и планировать свое время. Важно знать все основные темы программы и иметь навыки решения различных задач. Необходимо также изучать примеры решения задач и использовать дополнительные учебные материалы, такие как учебники и пособия.
Какие советы можно дать для успешной подготовки к ЕГЭ по математике база?
Для успешной подготовки к ЕГЭ по математике база полезно следовать нескольким советам. Во-первых, регулярно повторять и практиковать материал. Во-вторых, использовать различные источники информации, такие как учебники, интернет-ресурсы и видеоуроки. В-третьих, решать много задач разной сложности, чтобы развить навыки решения задач на экзамене. И, наконец, не забывать про отдых и здоровый образ жизни, так как физическое и психическое состояние влияют на успех в подготовке и сдаче экзамена.
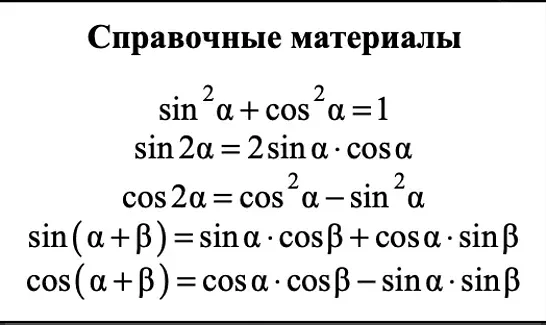


Статья очень полезная и информативная. Рассмотрены основные темы и правила подготовки к ЕГЭ по математике. Все объяснено доступным языком, что особенно важно для меня, так как математика не является моей сильной стороной. Очень понравилось, что автор статьи подчеркнул важность практики и регулярных занятий. Я согласен с автором, что без постоянной тренировки и решения задач невозможно достичь хороших результатов на ЕГЭ. Также автор дал несколько полезных советов по выбору основных тем и использованию учебников и задачников. Буду придерживаться этих рекомендаций при подготовке к экзамену. В общем, статья помогла мне разобраться с основами подготовки к ЕГЭ по математике и дала мне мотивацию начать тренироваться. Спасибо автору за такую полезную информацию!
Статья дает полное представление о том, что нужно знать для успешной сдачи ЕГЭ по математике. Она освещает основные темы и правила подготовки, что очень важно для меня, как будущего выпускника. Я узнаю, что для успешной подготовки необходимо изучить основные понятия и методы решения задач. Материал разбит на блоки, что упрощает процесс усвоения информации. Стали очевидны основные темы экзамена, такие как алгебра, геометрия и функции. Я понимаю, что для успешной подготовки мне необходимо уделить равное внимание каждой из этих тем. Важно усвоить все правила и формулы, чтобы уверенно решать задачи. Автор статьи подчеркивает необходимость регулярных тренировок. Он рекомендует решать большое количество задач из разных источников, чтобы привыкнуть к разным типам заданий и научиться работать с ними. Также, я узнаю о необходимости использования специальных учебников и пособий, которые помогут разобраться в трудных моментах. Очень полезной информацией стала рекомендация изучать предыдущие годы ЕГЭ. Таким образом, я смогу ознакомиться с типичными заданиями, структурой и форматом экзамена. Это поможет мне подготовиться к экзамену и улучшить свои шансы на успех. В целом, статья дает мне ясное представление о том, что нужно знать и как готовиться к ЕГЭ по математике. Она стала для меня настоящим помощником и мотивацией для серьезной подготовки. Я уверен, что придерживаясь рекомендаций автора, я смогу успешно сдать экзамен и достичь своих целей.