Что означает математическое ожидание равное нулю
Содержимое
- 1 Что означает математическое ожидание равное нулю
- 1.1 Математическое ожидание равное нулю: понятие и значение
- 1.2 Определение и основные принципы
- 1.3 Значение математического ожидания равного нулю
- 1.4 Примеры математического ожидания равного нулю
- 1.5 Пример 1: Бросок симметричной монеты
- 1.6 Видео по теме:
- 1.7 Вопрос-ответ:
- 1.7.0.1 Зачем нужно математическое ожидание равное нулю?
- 1.7.0.2 Как вычислить математическое ожидание равное нулю?
- 1.7.0.3 Можете привести пример случайной величины с математическим ожиданием равным нулю?
- 1.7.0.4 Какие свойства имеет математическое ожидание равное нулю?
- 1.7.0.5 Может ли математическое ожидание равное нулю быть отрицательным?
- 1.7.0.6 Зачем нужно математическое ожидание?
- 1.8 Пример 2: Выбор случайного числа из диапазона
- 1.9 Пример 3: Распределение вероятностей
Математическое ожидание, равное нулю, означает, что в среднем значение случайной величины равно нулю. Это может указывать на симметричность распределения или отсутствие смещения в данных. Узнайте, как определить математическое ожидание и его значения в контексте статистики и вероятности.
Математическое ожидание — это одна из основных концепций в математической статистике, которая позволяет рассчитать среднее значение случайной величины. Если математическое ожидание равно нулю, это означает, что среднее значение случайной величины равно нулю на основе вероятностных расчетов.
Математическое ожидание равное нулю может иметь различные интерпретации и применения в разных областях. Например, в теории вероятностей и статистике, математическое ожидание равное нулю может указывать на отсутствие смещения или среднего значения в данных, что может быть полезно при анализе и интерпретации результатов исследования.
Примером математического ожидания равного нулю может служить случай, когда подбрасывается симметричная монета. Вероятность выпадения орла или решки равна 0.5. Если мы будем подбрасывать монету множество раз, то среднее значение выпадения орла и решки будет стремиться к нулю, так как вероятности выпадения обоих сторон равны.
В других областях математическое ожидание равное нулю может иметь и другие значения и значения, например, в теории информации и теории игр. Знание и понимание математического ожидания равного нулю является важным элементом для анализа и интерпретации данных и результатов исследований в различных научных и практических областях.
Математическое ожидание равное нулю: понятие и значение
Значение математического ожидания равное нулю имеет важное значение в различных областях, включая теорию вероятностей, статистику и финансовую математику. Это позволяет анализировать и описывать случайные величины, оценивать вероятности и прогнозировать результаты различных событий.
Примеры:
1. Рассмотрим случайную величину, которая принимает значения -1 и 1 с вероятностями 0.5. Тогда математическое ожидание будет равно:
E(X) = (-1) * 0.5 + 1 * 0.5 = 0
2. Вероятность выпадения орла или решки при подбрасывании монеты равна 0.5 для каждого из этих значений. Если случайная величина принимает значение 1, если выпадает орел, и значение -1, если выпадает решка, то математическое ожидание будет:
E(X) = (1) * 0.5 + (-1) * 0.5 = 0
Таким образом, математическое ожидание равное нулю показывает, что в среднем случайная величина не имеет наклонности к определенному значению и равновероятно принимает положительные и отрицательные значения.
Определение и основные принципы
Основные принципы, связанные с математическим ожиданием равным нулю, включают:
- Симметрия распределения: Если случайная величина имеет симметричное распределение относительно нуля, тогда математическое ожидание будет равно нулю. Например, нормальное распределение с математическим ожиданием равным нулю будет симметричным относительно нуля.
- Отсутствие смещения: Если случайная величина не имеет смещения в одну из сторон, то математическое ожидание будет равно нулю. Например, если случайная величина имеет равные вероятности быть положительной или отрицательной, то математическое ожидание будет равно нулю.
- Ансамблевое среднее: Если случайная величина является частью ансамбля случайных величин, и каждая из них имеет математическое ожидание равное нулю, то математическое ожидание для всего ансамбля также будет равно нулю.
Наличие математического ожидания равного нулю может быть полезным в контексте статистических методов и анализа данных. Оно может указывать на отсутствие смещения или симметрии в распределении случайной величины. Также оно может служить базовым показателем для дальнейших расчетов и статистических выводов.
Значение математического ожидания равного нулю
Математическое ожидание равное нулю может иметь различные интерпретации в зависимости от контекста. В некоторых случаях это может означать, что положительные и отрицательные значения случайной величины компенсируют друг друга в среднем и в результате получается ноль. Например, если случайная величина представляет доходы и расходы, то математическое ожидание равное нулю может означать, что в среднем доходы и расходы равны друг другу.
В других случаях, математическое ожидание равное нулю может означать, что случайная величина имеет равную вероятность принимать как положительные, так и отрицательные значения. Например, если случайная величина представляет прибыль или убыток от инвестиций, то математическое ожидание равное нулю может означать, что в среднем инвестиции не приносят прибыли и не причиняют убытков.
Однако, значение математического ожидания равное нулю не всегда указывает на отсутствие среднего значения. В некоторых случаях, математическое ожидание может быть равно нулю, но иметь разброс значений вокруг этого значения. Например, если случайная величина имеет равную вероятность принимать значения -1 и 1, то ее математическое ожидание будет равно нулю, но это не означает, что все значения равны нулю.
Примеры математического ожидания равного нулю
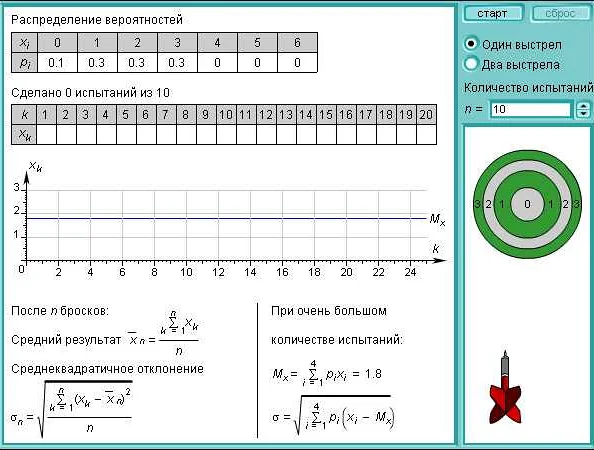
ПримерВероятностьЗначение случайной величины
| Монетка | 0.5 | -1 |
| 0.5 | 1 | |
| Кубик | 1/6 | -3 |
| 1/6 | -2 | |
| 1/6 | -1 | |
| 1/6 | 1 | |
| 1/6 | 2 | |
| 1/6 | 3 |
В первом примере рассмотрим случай подбрасывания монетки. С вероятностью 0.5 выпадает орёл (значение -1) и с вероятностью 0.5 выпадает решка (значение 1). Математическое ожидание в данном случае будет равно 0, так как (-1 * 0.5) + (1 * 0.5) = 0.
Во втором примере рассмотрим случай бросания кубика. С вероятностью 1/6 выпадает число -3, с вероятностью 1/6 выпадает число -2, с вероятностью 1/6 выпадает число -1, с вероятностью 1/6 выпадает число 1, с вероятностью 1/6 выпадает число 2 и с вероятностью 1/6 выпадает число 3. Математическое ожидание в данном случае также будет равно 0, так как ( (-3 * 1/6) + (-2 * 1/6) + (-1 * 1/6) + (1 * 1/6) + (2 * 1/6) + (3 * 1/6) = 0.
Это лишь примеры, которые помогут лучше понять суть математического ожидания равного нулю. В реальных задачах и экспериментах также можно столкнуться с этим показателем равным нулю, что говорит о сбалансированности средних значений случайной величины.
Пример 1: Бросок симметричной монеты

При броске монеты у нас есть два возможных исхода: выпадение орла (О) или выпадение решки (Р). Обозначим вероятность выпадения орла как p(О) и вероятность выпадения решки как p(Р). Так как монета симметрична, то p(О) = p(Р) = 0.5.
Теперь вычислим математическое ожидание для данного примера. В данном случае, мы можем рассчитать математическое ожидание, используя следующую формулу:
ИсходОценка
| О | 1 |
| Р | -1 |
В данной таблице указаны оценки для каждого возможного исхода. Вероятность для каждого исхода равна 0.5. Теперь, чтобы вычислить математическое ожидание, мы должны умножить каждую оценку на соответствующую вероятность и просуммировать результаты:
Математическое ожидание = (Оценка(О) * p(О)) + (Оценка(Р) * p(Р)) = (1 * 0.5) + (-1 * 0.5) = 0
Таким образом, в данном примере математическое ожидание равно нулю, что означает, что в среднем мы ожидаем получить одинаковый результат как орел, так и решка.
Видео по теме:
Вопрос-ответ:
Зачем нужно математическое ожидание равное нулю?
Математическое ожидание равное нулю используется для определения центра распределения случайной величины. Оно помогает понять, какие значения случайной величины чаще всего будут близки к нулю, а какие — наоборот, будут далеки от него.
Как вычислить математическое ожидание равное нулю?
Для вычисления математического ожидания нужно умножить каждое возможное значение случайной величины на его вероятность и сложить все полученные произведения. Если полученная сумма равна нулю, то математическое ожидание равно нулю.
Можете привести пример случайной величины с математическим ожиданием равным нулю?
Да, конечно. Например, рассмотрим случайную величину, которая может принимать значения -1 и 1 с вероятностью 0.5 каждое. В этом случае математическое ожидание будет равно 0, так как (-1 * 0.5) + (1 * 0.5) = 0.
Какие свойства имеет математическое ожидание равное нулю?
Математическое ожидание равное нулю имеет несколько свойств. Во-первых, если случайная величина имеет симметричное распределение относительно нуля, то ее математическое ожидание будет равно нулю. Во-вторых, если математическое ожидание случайной величины равно нулю, то среднее значение всех ее возможных значений также будет равно нулю.
Может ли математическое ожидание равное нулю быть отрицательным?
Нет, математическое ожидание равное нулю не может быть отрицательным. Математическое ожидание представляет собой среднее значение случайной величины, и если все значения случайной величины положительны или нулевые, то среднее значение тоже будет положительным или нулевым.
Зачем нужно математическое ожидание?
Математическое ожидание — это важная характеристика случайной величины, которая позволяет предсказывать ее среднее значение или ожидаемый результат. Оно является основой для многих статистических исследований и позволяет оценивать вероятности различных исходов.
Пример 2: Выбор случайного числа из диапазона
Рассмотрим ситуацию, когда мы выбираем случайное число из диапазона. Пусть у нас есть диапазон чисел от 1 до 10, и мы хотим выбрать одно число из этого диапазона.
Математическое ожидание равное нулю в данном случае означает, что среднее значение выбранного числа будет равно 0.
Однако, в данном примере, ноль не входит в наш диапазон чисел. Поэтому математическое ожидание равное нулю не имеет практического значения в этом контексте.
Пример 3: Распределение вероятностей

Рассмотрим пример, в котором математическое ожидание равно нулю для случайной величины, имеющей определенное распределение вероятностей.
Допустим, у нас есть следующая таблица с вероятностями:
ЗначениеВероятность
| 1 | 0.25 |
| -1 | 0.25 |
| 2 | 0.25 |
| -2 | 0.25 |
Для расчета математического ожидания, нужно умножить каждое значение случайной величины на соответствующую вероятность и сложить полученные произведения:
Математическое ожидание:
E(X) = 1 * 0.25 + (-1) * 0.25 + 2 * 0.25 + (-2) * 0.25 = 0
Таким образом, в данном примере математическое ожидание случайной величины равно нулю.
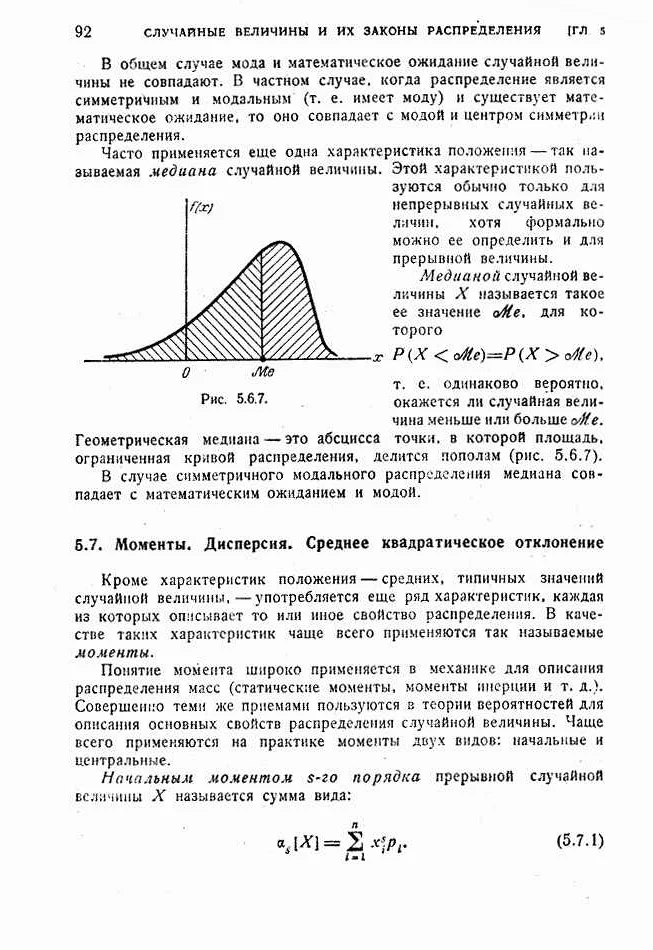




Математическое ожидание равное нулю — это понятие из математической статистики, которое означает, что среднее значение случайной величины равно нулю. Это может показаться странным, особенно если мы говорим о реальном явлении или эксперименте. Но в математике это вполне возможно и имеет свои объяснения. Нулевое математическое ожидание может быть результатом симметричного распределения данных относительно нуля. То есть положительные и отрицательные значения равновероятно встречаются и среднее значение получается равным нулю. Другой пример — случайная величина, которая принимает значения с равной вероятностью выше и ниже нуля. Например, если мы имеем дело с бесконечной последовательностью подбрасываний монеты, где орел равновероятно выпадает на каждом шаге, а решка также равновероятно выпадает на каждом шаге, то среднее значение будет равно нулю. Таким образом, нулевое математическое ожидание — это всего лишь одно из возможных значений, которое могут иметь случайные величины, и оно может быть объяснено симметрией или равновероятностью значений.
Математическое ожидание равное нулю означает, что среднее значение случайной величины равно нулю. Это может иметь различные интерпретации в разных контекстах. Например, если речь идет о распределении вероятностей, то это означает, что существует равная вероятность получить как положительные, так и отрицательные значения. В реальной жизни можно найти много примеров, где математическое ожидание равно нулю. Например, если мы рассматриваем доходы и расходы на определенный период времени, то средний доход может быть равен нулю, если доходы и расходы компенсируют друг друга. Также, в случае генетических исследований, если речь идет о генотипе, где один аллель относится к положительному эффекту, а другой — к отрицательному, то среднее значение будет равно нулю. Математическое ожидание равное нулю может быть полезным при анализе данных, так как оно позволяет установить справедливость и сбалансированность распределения, а также помогает в предсказании вероятностных событий.
Математическое ожидание, равное нулю, в математике означает, что в среднем значение случайной величины равно нулю. Это может показать, что на самом деле нет отклонений от среднего значения. Например, представьте, что вы подбрасываете симметричную монету. Вероятность выпадения орла или решки в каждом броске равна 0,5. Если вы подбросите монету много раз, среднее значение числа выпадений орла будет равно нулю. Это означает, что в среднем вы получаете одинаковое количество орлов и решек. Математическое ожидание равное нулю может быть полезным для определения симметрии или равномерности случайных величин.
Математическое ожидание равное нулю означает, что в среднем ожидаемое значение случайной величины равно нулю. В контексте статистики и вероятности это показатель, который помогает нам понять, каким образом случайная величина будет вести себя в долгосрочной перспективе. Давайте рассмотрим пример, чтобы это проиллюстрировать. Представьте, что у нас есть монета, которую мы подбрасываем. Вероятность выпадения орла и решки равна 0,5 каждому и мы хотим вычислить математическое ожидание. Для этого нужно умножить каждую возможную выпавшую сторону на ее вероятность и сложить результаты. В нашем случае это будет: (0,5 * (-1)) + (0,5 * 1) = 0. Таким образом, математическое ожидание равно нулю. Важно понимать, что математическое ожидание равное нулю не означает, что каждый раз при испытании мы получим ноль. Это просто говорит о том, что в долгосрочной перспективе сумма результатов будет равна нулю. Это понятие помогает нам анализировать и предсказывать поведение случайных величин и принимать важные решения на основе этих данных.