Что повторить для огэ по математике

Узнайте, какие темы и задачи важно повторить перед экзаменом по математике ОГЭ. Получите полезные советы и рекомендации для успешной подготовки и уверенного сдачи экзамена.

Основной экзамен по математике в рамках Обязательного государственного экзамена (ОГЭ) является одним из самых важных испытаний для школьников. Подготовка к данному экзамену требует серьезного и систематического подхода, а также повторения основных математических понятий и умений.

Важно помнить, что успешная подготовка к ОГЭ по математике требует не только знания формул и правил, но и умения применять их в различных задачах. Поэтому важно не только повторить основные темы, но и решить большое количество задач разной сложности.

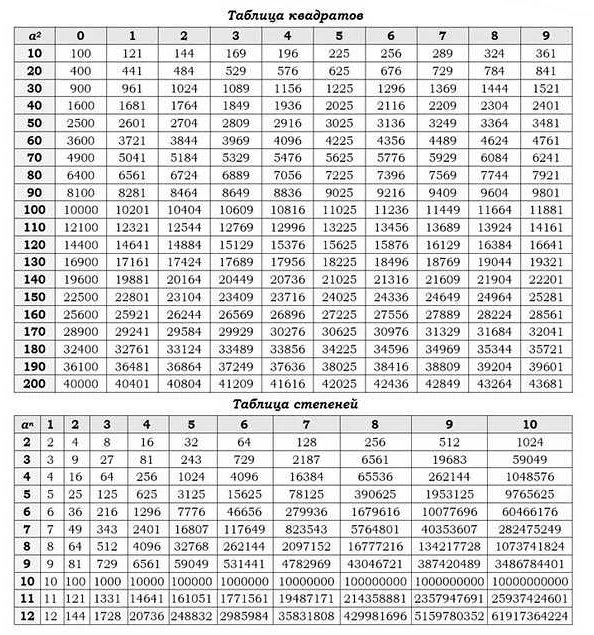
Одной из ключевых тем, которые следует повторить перед ОГЭ по математике, является арифметика. Вспомните основные операции (сложение, вычитание, умножение, деление) и правила их применения. Также обратите внимание на работу с дробями, процентами, десятичными дробями и правила округления чисел.

Кроме арифметики, важно повторить основы алгебры. Основные понятия, такие как переменная, уравнение, неравенство, многочлены и их операции, следует усвоить и научиться применять в задачах. Также обратите внимание на системы линейных уравнений и неравенств, которые встречаются в заданиях на ОГЭ.

Подготовка к ОГЭ по математике требует не только знания формул и правил, но и умения применять их в различных задачах.

Другой важной темой для повторения является геометрия. Необходимо вспомнить основные понятия, такие как угол, прямая, отрезок, треугольник, круг и т.д. Также стоит повторить свойства геометрических фигур, формулы для вычисления площадей и объемов различных фигур. Кроме того, обратите внимание на задачи с использованием теоремы Пифагора и теоремы Талеса.

Наконец, не забывайте о задачах на графики и таблицы. Умение читать и анализировать данные, представленные в графической или табличной форме, является важным навыком, который пригодится не только на экзамене, но и в реальной жизни. Повторите основные типы графиков (столбчатые, круговые, линейные) и умение анализировать их данные.

ОГЭ по математике: подготовка к экзамену

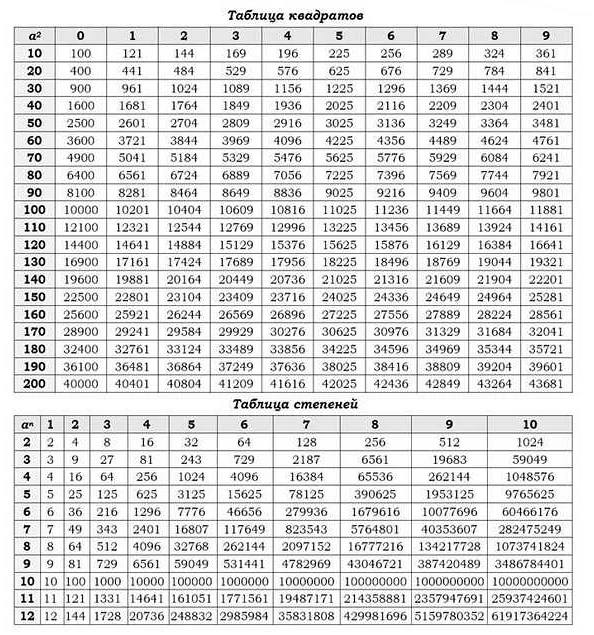
1. Изучите программу. Ознакомьтесь с темами и разделами, которые будут включены в экзаменационный билет. Уделите особое внимание сложным или непонятным темам и узким моментам.

2. Выделите время на повторение материала. Разделите свое время на периоды изучения нового материала и повторения ранее изученного. Повторение поможет закрепить знания и улучшить понимание темы.

3. Практикуйтесь в решении задач. Регулярные тренировки помогут вам стать более уверенным в решении различных типов задач. Используйте разнообразные источники задач, такие как учебники, рабочие тетради и интернет-ресурсы.

4. Обратите внимание на типичные ошибки. Изучите свои ошибки и попытайтесь разобраться в них. Это поможет вам избегать аналогичных ошибок в будущем.

5. Не забывайте о времени. ОГЭ по математике имеет определенное ограничение времени. Учите и практикуйтесь в решении задач с учетом этого ограничения, чтобы быть готовыми к экзамену.

6. Сотрудничайте с другими. Обсуждайте математические задачи с одноклассниками или учителем. Взаимодействие с другими студентами поможет вам лучше понять материал и найти новые подходы к решению задач.

7. Пользуйтесь подсказками. Если вы застряли на задаче, не стесняйтесь обратиться за помощью к учителю или однокласснику. Они могут предложить новый взгляд или подсказать подход к решению.

8. Самооценка. Регулярно проверяйте свои знания и умения, решая тесты и задачи. Оценивайте свои результаты и делайте выводы, где вам нужно улучшиться.

Следуя этим советам и рекомендациям, вы сможете успешно подготовиться к ОГЭ по математике и справиться с экзаменом без проблем. Удачи!

Теория множеств и логика

Теория множеств занимается изучением множеств и их свойств. Множество — это совокупность элементов, объединенных общим признаком. Основные операции над множествами включают объединение, пересечение, разность и дополнение. Также важно знать понятия подмножества, принадлежности и мощности множества.

Логика изучает правила и законы мысли, позволяющие строить доказательства и рассуждения. В математике часто используются логические связки, такие как «и», «или», «не». Также важно уметь работать с кванторами «существует» и «для любого». Кроме того, стоит ознакомиться с понятиями истинности и ложности высказываний, а также с тождественными и логическими эквивалентностями.

Основы теории множеств и логики будут полезны при решении задач по математике, особенно связанных с комбинаторикой, вероятностью и доказательствами. Поэтому рекомендуется уделить достаточно времени изучению этих разделов и проводить практические задания для закрепления материала.

Алгебраические выражения и уравнения

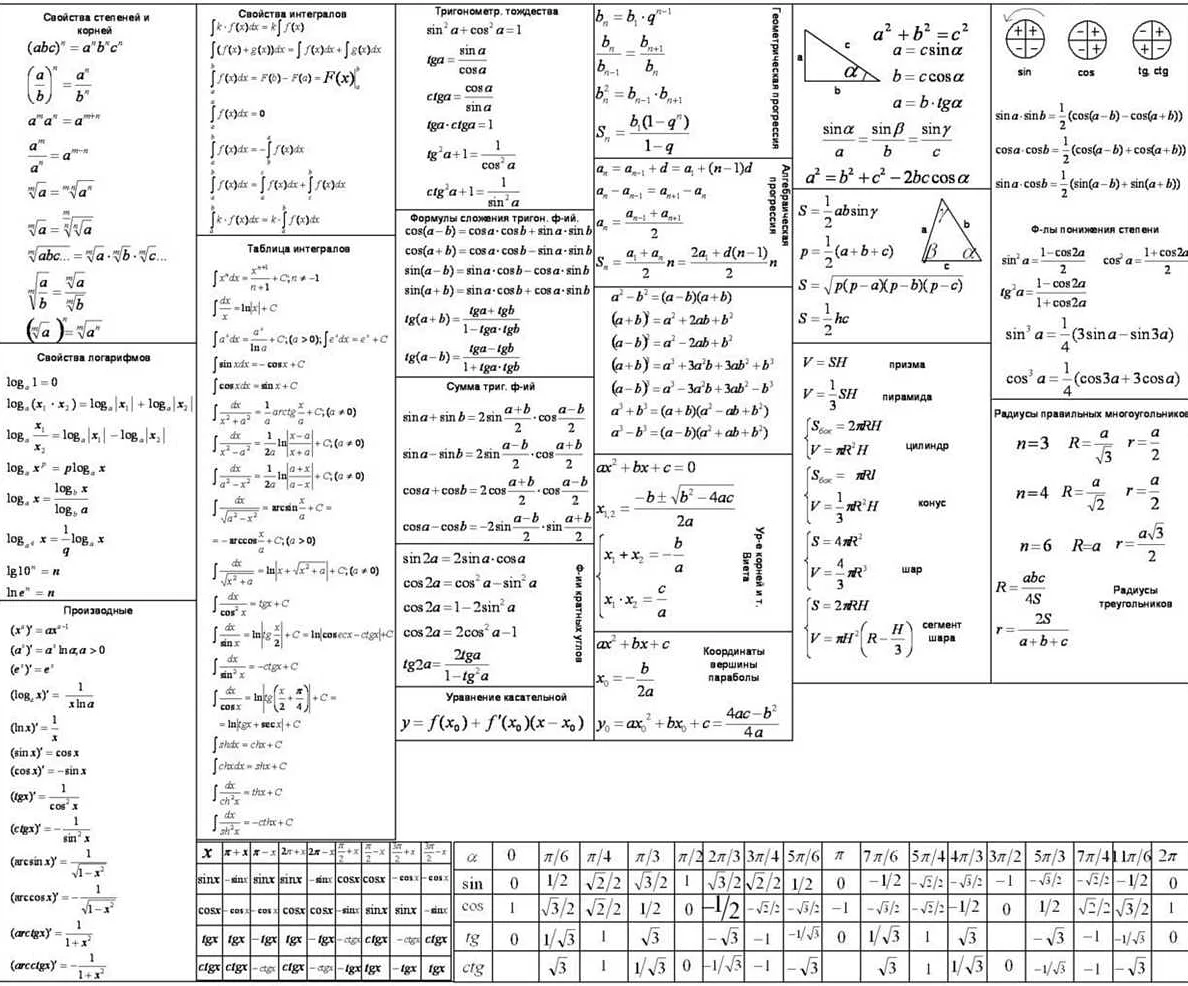
Для работы с алгебраическими выражениями необходимо знать основные свойства операций, такие как коммутативность, ассоциативность и дистрибутивность. Применение этих свойств позволяет упростить выражения и решить задачи более эффективно.

Уравнения представляют собой равенства, в которых одна или несколько переменных связаны друг с другом. Решение уравнений требует применения алгебраических методов, таких как раскрытие скобок, сокращение подобных членов и перемещение переменных.

Важно уметь распознавать тип уравнения, так как для каждого типа существуют специфические методы решения. Некоторые из основных типов уравнений включают линейные, квадратные и системы уравнений.

Подготовка к ОГЭ по математике включает в себя тренировку навыков работы с алгебраическими выражениями и уравнениями. Разбор теории и решение практических задач помогут укрепить понимание этих тем и успешно справиться с экзаменом.

Геометрия: фигуры и преобразования

Одно из основных преобразований — это поворот. При повороте фигуры вокруг определенной точки все ее точки смещаются по окружности. Угол поворота может быть положительным (по часовой стрелке) или отрицательным (против часовой стрелки).

Другим важным преобразованием является симметрия. Симметрия относительно оси — это такое преобразование, при котором каждая точка фигуры симметрично отражается относительно оси. Симметрия может быть вертикальной, горизонтальной или центральной.

Кроме того, геометрия изучает такие фигуры, как треугольники, прямоугольники, квадраты, круги и многоугольники. Для каждой фигуры существуют определенные свойства, которые позволяют их классифицировать и решать задачи на их основе.

Для подготовки к ОГЭ по математике необходимо повторить основные геометрические понятия, свойства фигур и преобразования. Также важно научиться применять полученные знания при решении задач, которые могут включать в себя как геометрические фигуры, так и преобразования.

Проценты и доли

Процент – это дробь, где числитель представляет собой часть от целого, а знаменатель равен 100. Проценты можно представить в виде десятичной дроби, разделив числитель на знаменатель и умножив результат на 100. Например, 25% можно записать как 0,25.

Доли – это части целого, которые представляются в виде дробей. Доля может быть меньше 1 (неправильная дробь), равна 1 (единичная дробь) или больше 1 (смешанная дробь). Например, 3/4 – это правильная дробь, 1 1/2 – это смешанная дробь.

Важно уметь переводить проценты в десятичные дроби и обратно, а также выполнять операции с процентами и долями. Для этого необходимо знать правила умножения, деления, сложения и вычитания десятичных дробей и дробей в общем виде.

Например, для нахождения процента от числа нужно умножить число на десятичную дробь, соответствующую проценту. Если нужно найти число, соответствующее определенному проценту, можно использовать формулу обратного преобразования.

Кроме того, нужно знать основные формулы и правила для работы с долями, такие как сложение, вычитание, умножение и деление дробей.

На ОГЭ по математике могут встретиться задачи, требующие знания процентов и долей. Поэтому важно повторить основные понятия и правила работы с ними, чтобы быть готовым к решению таких задач.

Статистика и вероятность

Статистика — это наука о сборе, анализе, интерпретации и представлении данных. Она помогает нам извлекать полезную информацию из больших объемов данных и делать уверенные выводы на основе этих данных. Важными понятиями в статистике являются: выборка, генеральная совокупность, среднее значение, медиана, мода, дисперсия и стандартное отклонение.

Вероятность — это раздел математики, который изучает случайные события и их вероятности. Она позволяет оценивать вероятность того или иного события и принимать решения на основе этой информации. Вероятность измеряется числом от 0 до 1, где 0 — событие невозможно, а 1 — событие обязательно произойдет. Вероятность может быть выражена в виде доли, процента или десятичной дроби.

Основными понятиями в вероятности являются: случайный эксперимент, элементарное событие, событие, пространство элементарных событий, вероятность события, условная вероятность и независимость событий. Также существует ряд методов для вычисления вероятности событий, таких как классическое определение вероятности, относительная частота и аксиоматическое определение.

Изучение статистики и вероятности поможет вам развить навыки критического мышления, логического анализа и принятия решений. При подготовке к экзамену по математике ОГЭ рекомендуется повторить основные понятия и методы статистики и вероятности, а также провести практические задания для закрепления знаний.

Функции и графики

График функции – это визуальное представление функции на координатной плоскости. Он состоит из точек, которые соответствуют значениям аргумента и значениям функции. Графики функций могут иметь различные формы: прямые, параболы, гиперболы и т.д. Знание формы и особенностей графиков различных функций позволяет анализировать их свойства и решать задачи, связанные с функциями.

Важно уметь определять основные характеристики графика функции, такие как: вершина параболы, асимптоты, точки пересечения с осями координат, максимальные и минимальные значения функции и т.д. Для этого необходимо знать основные методы работы с графиками функций, такие как построение графика, определение его формы и нахождение значений функции по графику.

На ОГЭ по математике часто встречаются задания, связанные с функциями и графиками. Это может быть задача на построение графика функции, определение значения функции или аргумента по графику, анализ свойств графика и другие. Поэтому важно хорошо подготовиться к данной теме и повторить основные понятия, правила и методы работы с функциями и графиками.

Рекомендуется изучить и понять основные типы функций и их графики, основные методы работы с графиками функций, а также основные свойства графиков функций. После этого решайте множество разнообразных задач и упражнений, чтобы закрепить полученные знания и навыки. Постепенно вы сможете стать более уверенными в решении задач, связанных с функциями и графиками, и успешно справиться с ОГЭ по математике.

Дроби и десятичные дроби

Перед началом изучения дробей необходимо разобраться с их основными понятиями. Дробь состоит из числителя и знаменателя, которые разделены горизонтальной чертой. Числитель — это число, которое находится над чертой, а знаменатель — число, которое находится под чертой.

Дроби могут быть как правильными, так и неправильными. Правильная дробь имеет числитель, который меньше знаменателя, в то время как неправильная дробь имеет числитель, который больше или равен знаменателю. Также существуют смешанные числа, которые состоят из целой части и дробной части.

Однако, помимо обычных дробей, существуют также десятичные дроби. Десятичная дробь — это число, записанное в десятичной системе счисления, которое может содержать как целую часть, так и дробную часть, отделенную запятой или точкой.

Для выполнения операций с дробями и десятичными дробями необходимо знать основные правила. Например, сложение и вычитание дробей требует приведения их к общему знаменателю. Умножение дробей выполняется путем перемножения числителей и знаменателей, а деление — путем умножения первой дроби на обратную второй. Также для работы с десятичными дробями необходимо знать правила округления и преобразования десятичной дроби в обыкновенную.

Повторение дробей и десятичных дробей перед экзаменом поможет укрепить понимание основных понятий и научиться решать задачи, связанные с этой темой. С помощью достаточной практики и понимания правил, можно успешно справиться с заданиями на экзамене и получить хороший результат.

Вопрос-ответ:

Какие основные темы нужно повторить для подготовки к ОГЭ по математике?

Для подготовки к ОГЭ по математике нужно повторить основные темы, такие как алгебра (работа с выражениями, уравнения, системы уравнений), геометрия (площади и объемы, пространственное мышление), статистика и вероятность (таблицы, графики, задачи на вероятность). Также важно повторить основные арифметические операции и правила работы с дробями.

Какие полезные материалы могут помочь в подготовке к ОГЭ по математике?

В подготовке к ОГЭ по математике могут помочь различные учебники, пособия и задачники по данному предмету. Также полезно решать тестовые задания и пробные работы, чтобы понять свой уровень подготовки и выявить слабые места. Кроме того, существуют онлайн-курсы и видеоуроки, которые можно использовать для самостоятельного изучения материала.

Как эффективно планировать время подготовки к ОГЭ по математике?

Для эффективного планирования времени подготовки к ОГЭ по математике рекомендуется составить расписание, в котором будет указано, сколько времени будет уделяться каждой теме. Важно также учитывать свои индивидуальные особенности и потребности. Например, если у вас есть слабые места в определенных темах, то следует уделить им больше времени.

Какие стратегии помогут успешно справиться с экзаменом по математике?

Для успешной сдачи экзамена по математике полезно использовать различные стратегии. Во-первых, стоит начать с решения задач, в которых вы уверены, чтобы набрать необходимое количество баллов. Затем можно переходить к более сложным задачам. Во-вторых, стоит уделить внимание работе над ошибками. Если вы совершите ошибку, необходимо понять, в чем состоит ошибка и как ее избежать в будущем. В-третьих, необходимо учитывать время и распределять его правильно между заданиями.

Сколько времени нужно уделить ежедневной подготовке к ОГЭ по математике?

Время, которое следует уделять ежедневной подготовке к ОГЭ по математике, зависит от уровня подготовки каждого конкретного ученика. В среднем рекомендуется уделять от 1 до 2 часов в день для повторения материала, решения задач, анализа ошибок и выполнения практических заданий.

Как организовать эффективную подготовку к ОГЭ по математике?

Для эффективной подготовки к ОГЭ по математике рекомендуется создать расписание, в котором уделить время на повторение основных тем, решение задач, анализ ошибок, выполнение практических заданий. Также важно использовать различные учебные материалы, найти репетитора или присоединиться к группе подготовки, чтобы получить дополнительную помощь и поддержку. Не забывайте также об организации коротких перерывов для отдыха и релаксации.

Какие темы по математике следует повторить перед ОГЭ?

Перед ОГЭ по математике стоит повторить такие темы, как: арифметические действия (сложение, вычитание, умножение, деление), дроби, проценты, пропорции, уравнения и неравенства, геометрия (площади и объемы фигур), статистика и вероятность. Также рекомендуется повторить основные приемы решения задач и умение анализировать условия задачи.

Системы счисления и основы теории чисел

Однако, помимо десятичной системы, существуют и другие системы счисления, такие как двоичная, восьмеричная и шестнадцатеричная. Например, в двоичной системе счисления используются только две цифры: 0 и 1. Эта система широко применяется в компьютерах и цифровой технике.

Важно знать, как переводить числа из одной системы счисления в другую. Для этого существуют различные алгоритмы и правила. Например, для перевода числа из двоичной системы в десятичную, нужно умножать каждую цифру числа на соответствующую ей степень числа 2 и складывать результаты.

Теория чисел включает в себя изучение свойств чисел: четности, кратности, делителей, простых чисел и т.д. Знание основ теории чисел поможет в решении различных задач по математике. Например, знание простых чисел поможет определить, является ли число простым или составным.

Успешная подготовка к ОГЭ по математике требует хорошего понимания систем счисления и основ теории чисел.

Видео по теме: