Что повторить перед огэ по математике

Узнайте, какие темы и принципы важно повторить перед ОГЭ по математике, чтобы успешно справиться с экзаменом. Получите советы по подготовке и рекомендации по выполнению заданий.

Единый государственный экзамен (ОГЭ) по математике является одним из самых важных испытаний для учеников. Этот экзамен проверяет не только знания учащихся, но и их навыки решения математических задач. Подготовка к ОГЭ требует систематического повторения материала и решения разнообразных задач.

Одной из главных тем для повторения перед ОГЭ является алгебра. Ученики должны вспомнить основные принципы работы с уравнениями и неравенствами, а также научиться решать системы линейных уравнений и неравенств. Также необходимо повторить понятия и свойства функций, включая линейные, квадратные и простейшие трансцендентные функции.

Геометрия также занимает важное место в программе ОГЭ по математике. Ученикам нужно повторить основные понятия геометрии, включая понятия прямой, отрезка, угла, треугольника, четырехугольника, окружности и т.д. Они также должны знать основные свойства этих фигур и уметь использовать их для решения задач.

Вероятность и статистика являются еще одной важной темой для повторения перед ОГЭ. Ученикам нужно знать основные понятия и правила комбинаторики, вероятности и статистики. Они должны уметь решать задачи на вычисление вероятности, определение среднего значения и вариации, а также анализ данных.

ОГЭ по математике: основные темы и задания

Ежегодно выпускники 9 классов проходят ОГЭ по математике, который проверяет их знания и навыки в этом предмете. ОГЭ по математике состоит из нескольких разделов, включающих в себя различные темы и типы заданий.

Одной из основных тем ОГЭ по математике является алгебра. В этом разделе выпускники решают задачи на работу с алгебраическими выражениями, уравнениями и неравенствами, системами уравнений. Также они знакомятся с понятием функции, графиками функций и их анализом.

Другая важная тема — геометрия. В этом разделе выпускники решают задачи на построение и анализ геометрических фигур, на вычисление площадей и объемов, а также на применение теоремы Пифагора и теоремы косинусов.

ОГЭ по математике также включает в себя задания на работу с числами и операциями над ними, на анализ и обработку статистических данных, на применение элементарных вероятностных моделей.

В каждом разделе ОГЭ по математике выпускники сталкиваются с различными типами заданий. Например, они могут решать задачи на нахождение значения переменной, на выбор правильного выражения или преобразование выражения, на построение графика функции или геометрической фигуры, на анализ данных и составление выводов. Кроме того, в ОГЭ по математике часто встречаются задания, требующие применения логических рассуждений и анализа условий задачи.

Для успешной подготовки к ОГЭ по математике рекомендуется повторить основные темы и типы заданий, изучить правила и приемы их решения, а также регулярно тренироваться на выполнение различных задач. Только так можно достичь хороших результатов и уверенно сдать экзамен.

Алгебра: формулы, уравнения, неравенства

Формулы – это математические выражения, которые связывают различные величины с помощью математических операций. Формулы могут быть использованы для решения задач в различных областях науки и техники. Важно уметь работать с формулами и преобразовывать их, чтобы получить нужную информацию или выразить одну величину через другую.

Уравнения – это математические выражения, в которых присутствует знак равенства. Уравнения могут иметь одно или несколько решений, которые позволяют найти значения неизвестных величин. Решение уравнения – это такое значение неизвестной, при котором обе части уравнения становятся равными. Важно уметь решать уравнения и проверять полученные значения.

Неравенства – это математические выражения, в которых присутствуют знаки неравенства (, ≤, ≥). Неравенства позволяют сравнить две величины или два математических выражения. Решением неравенства является множество значений, при которых выполнено данное неравенство. Важно уметь решать неравенства и определять их множества решений.

ТемаОписание

Формулы	Изучение и преобразование математических формул, применение формул в задачах
Уравнения	Решение уравнений различных типов, проверка полученных решений
Неравенства	Решение неравенств различных типов, определение множества решений

Освоение этих тем позволит успешно справиться с заданиями по алгебре на ОГЭ по математике. Рекомендуется повторить основные правила и методы работы с формулами, уравнениями и неравенствами, а также решить достаточное количество практических заданий для закрепления навыков и уверенности в своих знаниях.

Геометрия: фигуры, площади, объемы

Площадь – это мера плоской фигуры, выражающаяся числом, которое характеризует, сколько квадратных единиц можно поместить на эту фигуру без наложений и пропусков. Изучая геометрию, необходимо уметь вычислять площади прямоугольников, треугольников, кругов и других фигур.

Объем – это мера трехмерной фигуры, выражающаяся числом, которое характеризует, сколько кубических единиц объема занимает данная фигура. Для вычисления объемов используются формулы для параллелепипедов, цилиндров, конусов и других фигур.

Понимание основных понятий и формул в геометрии позволит решать различные задачи, связанные с вычислением площадей и объемов фигур. Необходимо уметь применять формулы, а также решать задачи, которые требуют применения геометрических знаний.

Помимо этого, важно уметь работать с различными единицами измерения и переводить значения площадей и объемов из одних единиц в другие. Необходимо быть внимательным при решении задач, чтобы правильно выбирать единицы измерения и проводить необходимые преобразования.

В заключение, для успешной подготовки к ОГЭ по математике необходимо повторить основные темы геометрии, включая вычисление площадей и объемов фигур, применение формул и решение задач. Регулярная практика и повторение помогут укрепить знания и уверенно справиться с экзаменом.

Тригонометрия: синусы, косинусы, тангенсы

Синус (sin) – это отношение противолежащего катета к гипотенузе в прямоугольном треугольнике. Синус угла можно вычислить с помощью соответствующего отношения.

Косинус (cos) – это отношение прилежащего катета к гипотенузе в прямоугольном треугольнике. Косинус угла также можно вычислить с помощью соответствующего отношения.

Тангенс (tg) – это отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике. Тангенс угла также можно вычислить с помощью соответствующего отношения.

Знание синусов, косинусов и тангенсов позволяет решать различные задачи, связанные с геометрией и тригонометрией.

Перед ОГЭ по математике рекомендуется повторить основные свойства и формулы, связанные с синусами, косинусами и тангенсами, а также выполнить практические задания для закрепления знаний.

Важно: Тригонометрия является одним из ключевых разделов математики и важным компонентом подготовки к ОГЭ по математике. Поэтому необходимо уделить достаточно времени для изучения этой темы и ее практического применения.

Вероятность и статистика: графики, таблицы, диаграммы

Один из основных инструментов вероятности и статистики — это графики, таблицы и диаграммы. Они позволяют визуализировать информацию и легче анализировать ее. Графики могут быть различных типов: столбчатые, круговые, линейные и т.д. Таблицы используются для систематизации данных, а диаграммы позволяют сравнивать и отображать взаимосвязи между различными показателями.

На ОГЭ по математике часто встречаются задания, связанные с анализом графиков, таблиц и диаграмм. Вам могут предложить построить график по заданным данным, анализировать представленную информацию, сравнивать и находить зависимости между показателями, решать задачи на основе представленных графиков и таблиц.

При подготовке к ОГЭ по математике рекомендуется повторить основные типы графиков, уметь строить графики по заданным данным, анализировать их и делать выводы. Также полезно освежить знания о таблицах и диаграммах, уметь работать с ними и решать задачи на основе представленных данных.

Знание основ вероятности и статистики, а также умение работать с графиками, таблицами и диаграммами помогут вам успешно справиться с заданиями по этой теме на ОГЭ по математике.

Функции: линейные, квадратичные, прогрессии

На ОГЭ по математике важно хорошо знать и уметь работать с различными типами функций. Особое внимание стоит уделить линейным и квадратичным функциям, а также прогрессиям.

Линейная функция представляет собой функцию вида y = kx + b, где k и b — константы. Она описывает прямую линию на графике и имеет постоянный наклон. Чтобы построить график линейной функции, достаточно знать значения k и b.

Квадратичная функция имеет вид y = ax^2 + bx + c, где a, b и c — константы. График такой функции представляет собой параболу. Важно уметь определять вершину параболы, направление ее выпуклости и симметричность относительно оси OY.

Прогрессия — это последовательность чисел, в которой каждый следующий элемент получается из предыдущего прибавлением или умножением на постоянное число. Особенно важно знать и уметь работать с арифметической и геометрической прогрессией. В арифметической прогрессии каждый следующий элемент получается прибавлением к предыдущему одного и того же числа, называемого разностью. В геометрической прогрессии каждый следующий элемент получается умножением предыдущего на одно и то же число, называемое знаменателем.

Итак, функции — это важная тема для подготовки к ОГЭ по математике. Уделите достаточно времени изучению линейных и квадратичных функций, а также прогрессий, и вы будете хорошо подготовлены к экзамену!

Видео по теме:

Вопрос-ответ:

Какие главные темы нужно повторить перед ОГЭ по математике?

Перед ОГЭ по математике стоит повторить следующие главные темы: алгебраические выражения и уравнения, геометрия, графики функций, статистика и вероятность.

Какие задания чаще всего встречаются на ОГЭ по математике?

На ОГЭ по математике чаще всего встречаются задания на решение уравнений, построение графиков функций, вычисление площадей и объемов, а также задания на работу с таблицами и графиками.

Какие методы и приемы решения задач полезно повторить перед ОГЭ по математике?

Перед ОГЭ по математике полезно повторить методы решения задач на нахождение неизвестных величин, методы решения уравнений и систем уравнений, методы построения графиков функций, а также методы решения задач на работу с данными в таблицах и графиках.

Какие ошибки стоит избегать при решении задач на ОГЭ по математике?

При решении задач на ОГЭ по математике стоит избегать ошибок в расчетах, неправильного применения формул и законов, неправильного чтения условия задачи, а также неправильного выбора метода решения задачи.

Какой подход к подготовке к ОГЭ по математике будет наиболее эффективным?

Наиболее эффективным подходом к подготовке к ОГЭ по математике будет регулярное повторение материала, решение большого количества задач разного уровня сложности, а также обратная связь — проверка и исправление ошибок, анализ проблемных моментов и их устранение.

Какие основные темы нужно повторить перед ОГЭ по математике?

Основные темы, которые нужно повторить перед ОГЭ по математике, включают такие разделы как алгебра (работа с выражениями, уравнениями и неравенствами), геометрия (планиметрия и стереометрия), статистика и вероятность, функции и графики, а также изучение графиков функций.

Анализ графиков и таблиц: экстремумы, интервалы

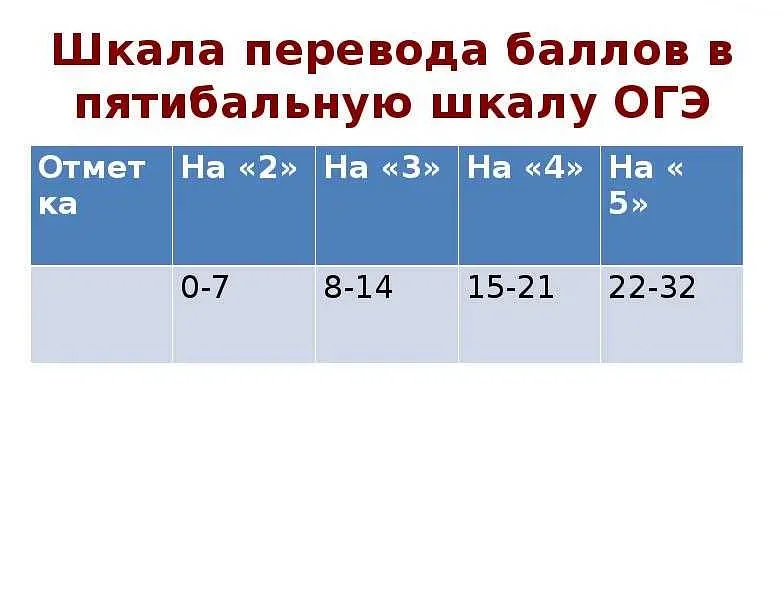
Для начала, давайте определимся с понятием экстремума. Экстремумом называется точка, в которой достигается максимальное или минимальное значение функции. Для анализа графиков и таблиц необходимо уметь определять координаты экстремумов и интервалы, на которых функция возрастает или убывает.

Для определения экстремумов и интервалов используют графики функций или таблицы значений функций. График функции представляет собой набор точек (x, y), где x — значение аргумента, y — значение функции. Таблица значений функции содержит значения аргумента и соответствующие значения функции.

Для определения экстремумов функции можно использовать производную функции. Если производная функции равна нулю или не существует в точке, то в этой точке может находиться экстремум. Для определения интервалов, на которых функция возрастает или убывает, необходимо исследовать знак производной функции на соответствующих интервалах.

Таблицы значений функции также позволяют определить экстремумы и интервалы. Для этого необходимо найти значения функции и анализировать их изменение. Если значения функции возрастают или убывают на определенном интервале, то можно говорить о наличии экстремума или интервала, на котором функция возрастает или убывает.

Важно уметь анализировать графики и таблицы, чтобы правильно определить экстремумы и интервалы. Для этого необходимо использовать полученные знания о производных функций, а также уметь анализировать изменение значений функции по таблице значений. При решении задач на анализ графиков и таблиц необходимо проявлять внимательность и точность, чтобы избежать ошибок.

Итак, анализ графиков и таблиц с учетом экстремумов и интервалов является важной темой перед ОГЭ по математике. Умение определять экстремумы и интервалы на графиках и таблицах позволяет более глубоко понять свойства функций и использовать эти знания при решении задач.

Задачи на логику и рассуждения

На ОГЭ по математике могут встретиться задачи, которые требуют логического мышления и умения рассуждать. Эти задачи проверяют вашу способность анализировать информацию, делать логические выводы и применять рассуждения для решения сложных задач.

Одним из типов задач на логику может быть задача с логическими операциями. Вам могут предложить несколько утверждений, и вам нужно определить, какие из них истинны, а какие ложны, и на основе этих утверждений сделать выводы.

Другой тип задач на логику — это задачи с последовательностями чисел или фигур. Вам могут предложить некоторую последовательность, и вам нужно найти закономерность, по которой эта последовательность формируется, и продолжить ее.

Также на ОГЭ часто встречаются задачи-головоломки, которые требуют смекалки и логического мышления. Вам могут задать загадку или задачу с условием, которое нужно разгадать или решить с помощью логики и рассуждений.

Для успешного решения задач на логику и рассуждения важно уметь анализировать информацию, выделять главное, делать выводы на основе имеющихся данных и применять логические законы. Практика решения разнообразных задач поможет вам развить эти навыки и подготовиться к ОГЭ по математике.