Что будет если разделить на 0 в высшей математике

Узнайте, что произойдет, если попытаться разделить на 0 в высшей математике. Разберем понятие бесконечности, асимптоты, неопределенности и другие интересные аспекты этого вопроса.

Разделение на ноль – одна из самых загадочных и интересных тем высшей математики. Уже на школьных уроках математики нам говорят, что разделить число на ноль нельзя. Но что произойдет, если все-таки попытаться это сделать?

Самое первое, что нужно знать, это то, что разделить на ноль нельзя. При попытке сделать это, мы получим бесконечность, и такая операция не имеет математического смысла. Впрочем, в некоторых случаях можно говорить о пределе при делении на ноль, но это уже относится к более сложным понятиям математического анализа.

«Получение бесконечности при делении на ноль является формальным способом сохранить непрерывность математических моделей и уравнений, но в реальной жизни подобное деление невозможно».

К примеру, если мы возьмем число 5 и разделим его на число, которое близко к нулю, то результат будет бесконечно большим. Если же мы возьмем число -5 и разделим его на число, которое близко к нулю, то результат будет бесконечно малым.

Что произойдет при делении числа на ноль в высшей математике?

Если числитель равен нулю, а знаменатель также равен нулю, то результат деления будет считаться неопределенным. Это означает, что нельзя однозначно определить какое число нужно получить в результате деления.

Если числитель отличен от нуля, а знаменатель равен нулю, то результат деления будет равен бесконечности. Например, если число 5 разделить на 0, то результатом будет бесконечность (5/0 = ∞).

Такие ситуации с делением на ноль возникают, например, при решении некоторых математических задач или в некоторых формулах. В высшей математике деление на ноль рассматривается с точки зрения аналитической геометрии, алгебры и математического анализа.

При проведении математических выкладок и решении задач важно помнить, что деление на ноль не имеет определенного значения и может привести к некорректным результатам.

ПримерРезультат деления

0 / 0	неопределенность
5 / 0	∞ (бесконечность)

Видео по теме:

Деление на ноль: определение и особенности

В основе определения деления на ноль лежит понятие предела. Если число a делится на число b, то предел отношения a/b при приближении b к нулю определяется величиной, бесконечно приближающейся к положительной или отрицательной бесконечности.

Основные особенности деления на ноль:

1. Если положительное число делить на ноль, результатом будет положительная бесконечность.
2. Если отрицательное число делить на ноль, результатом будет отрицательная бесконечность.
3. Если ноль делить на ноль, результатом будет неопределенность или неопределенное значение. В этом случае, результат может зависеть от контекста и условий задачи.

Деление на ноль является одной из неразрешимых проблем в математике, и его результат может быть неоднозначным. Поэтому, при решении математических задач, в которых возникает деление, необходимо учитывать особенности и контекст задачи для получения корректного результата.

Значимость нуля в математике

Ноль является основой для развития арифметических операций. Он является нейтральным элементом для сложения и вычитания, и любое число, прибавленное к нулю или вычтенное из нуля, остается неизменным. Также, умножение на ноль дает ноль, что является важным свойством для ряда математических операций.

Ноль также играет важную роль в делении. Если число разделить на ноль, результатом будет неопределенность. Это связано с тем, что в математике невозможно разделить одно число на ноль и получить однозначный результат. В этом случае, результат деления может быть равен бесконечности или неопределенной величине.

Ноль также играет важную роль в представлении чисел и понятии нулевого элемента. Он используется для обозначения отсутствия или пустоты, и важен для формулирования различных математических концепций и теорий.

Таким образом, ноль в математике является неотъемлемой частью и имеет глубокое значение для развития и понимания различных математических концепций и операций.

Частные случаи деления на ноль

Один из таких частных случаев – деление числа на ноль в пределе. Рассмотрим, например, предел функции f(x) = 1/x при x стремящемся к нулю. В данном случае, предел равен плюс или минус бесконечности, в зависимости от знака числа x.

Другим примером является деление комплексного числа на ноль. В комплексной алгебре существует понятие бесконечности, которое может быть использовано для описания деления на ноль. В этом случае, результатом деления комплексного числа на ноль будет бесконечность с определенным аргументом.

Важно отметить, что подобные частные случаи имеют теоретическое значение и применяются в некоторых областях математики и физики. Однако, в реальной жизни деление на ноль считается ошибкой и может привести к непредсказуемым результатам или противоречиям.

Деление на ноль в арифметике

В обычной арифметике, деление на ноль запрещено и не имеет смысла. При попытке разделить число на ноль, результатом будет ошибка или бесконечность. Это связано с тем, что ноль не имеет обратного значения, то есть нет такого числа, при умножении на которое мы получим ноль.

В высшей математике существует понятие «расширенных чисел», где деление на ноль определено. Но даже в этом случае, результатом деления на ноль будет неопределенность или бесконечность. Расширенные числа позволяют работать с бесконечностями и асимптотами, но они не решают проблему деления на ноль.

В итоге, деление на ноль остается математической загадкой и вызывает множество противоречивых и неопределенных результатов. Поэтому, в арифметике и математике в целом, деление на ноль следует избегать и рассматривать как ошибку или неопределенность.

Деление на ноль в алгебре и геометрии

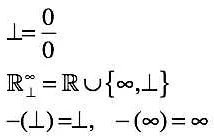
В алгебре, деление на ноль является неопределенностью. Это означает, что не существует однозначного значения, которое можно было бы присвоить результату такого деления. Например, если попытаться разделить число на ноль, то результатом будет неопределенное значение.

Однако в некоторых случаях, в алгебре можно дать определенное значение для деления на ноль. Например, в теории пределов, вводится понятие бесконечности, и можно говорить о том, что результат деления числа на ноль стремится к бесконечности. Это позволяет решать некоторые математические задачи и делает такое деление полезным инструментом в алгебре.

В геометрии деление на ноль также имеет свои особенности. Например, если попытаться разделить длину отрезка на ноль, то результатом будет бесконечность. Это можно объяснить тем, что при делении на ноль, отрезок стремится к бесконечности, то есть становится бесконечно длинным.

Однако в геометрии также возникают ситуации, когда деление на ноль не имеет смысла. Например, если попытаться разделить площадь круга на ноль, то результатом будет неопределенность, так как невозможно разделить площадь на отсутствие единицы измерения.

Таким образом, деление на ноль в алгебре и геометрии имеет свои особенности и может привести как к определенным значениям, так и к неопределенностям в зависимости от контекста задачи.

Деление на ноль в анализе

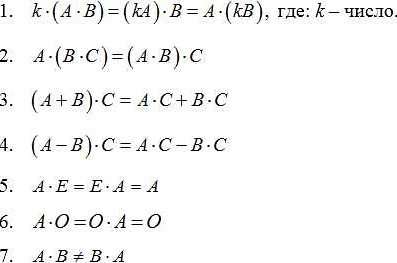
В анализе, деление на ноль считается неопределенным. Это означает, что нельзя однозначно определить результат такой операции. Попытка деления на ноль приводит к появлению бесконечно больших или бесконечно малых значений, что не согласуется с основными принципами математики и логики.

Одно из основных применений анализа — изучение пределов функций. При рассмотрении предела функции f(x) при x стремящемся к некоторому значению a, существует несколько возможных исходов:

1. Предел существует и конечен: В этом случае можно однозначно определить значение функции в точке a. Деление на ноль в этом случае не возможно, так как функция будет иметь определенное значение во всех точках окрестности a.

2. Предел равен плюс или минус бесконечности: В этом случае функция может стремиться к плюс или минус бесконечности при приближении к точке a. Опять же, деление на ноль не возможно, так как функция принимает различные значения, но не может достичь бесконечности.

3. Предел не существует: В этом случае функция не имеет предела в точке a. В таком случае, деление на ноль не имеет смысла, так как функция может принимать различные значения около точки a, но не имеет однозначного значения в этой точке.

Таким образом, деление на ноль в анализе является недопустимой операцией и противоречит основным принципам математики. Все выкладки и доказательства в анализе строятся на основе корректных математических операций, и деление на ноль не входит в их число.

Последствия деления на ноль в математике

В математическом анализе, деление на ноль может привести к появлению бесконечностей или расходимостей. Например, при делении числа на очень маленькое число, результат может стремиться к бесконечности. Это связано с понятием предела и бесконечности в математике.

В некоторых случаях, деление на ноль может привести к математическим противоречиям и некорректным результатам. Например, при решении уравнения, которое включает деление на ноль, можно получить противоречивые решения или несуществующие значения.

Однако, в математике существуют специальные концепции, такие как теория пределов и аналитическая геометрия, которые позволяют изучать деление на ноль и его последствия в более строгом и формальном контексте. Эти концепции позволяют определить и изучить поведение математических функций и уравнений в окрестности нуля.

В заключение, деление на ноль в высшей математике может иметь различные последствия и свойства, которые могут быть изучены и поняты с помощью специальных математических концепций и теорий. Это делает тему деления на ноль одной из наиболее интересных и сложных в математике.

Выводы о делении на ноль в высшей математике

В высшей математике деление на ноль рассматривается как невозможная операция. При делении любого числа на ноль не существует определенного результата, и это противоречит основным принципам математики.

Деление на ноль приводит к появлению неопределенностей и противоречий в математических выражениях и уравнениях. Математики долгое время пытались разрешить эту проблему, но до сих пор не смогли найти единообразного и приемлемого решения.

В контексте аналитической геометрии, деление на ноль приводит к возникновению бесконечно удаленных точек и неопределенных геометрических объектов. Таким образом, деление на ноль нарушает основные законы геометрии.

Однако, в некоторых случаях математики используют пределы и асимптоты, чтобы аппроксимировать результат деления на ноль. Например, в дифференциальном и интегральном исчислении возможно определить пределы функций при приближении к нулю. Это позволяет изучать поведение функций вблизи нуля, хотя само деление на ноль остается недопустимым.

Таким образом, выводы о делении на ноль в высшей математике сводятся к тому, что деление на ноль не имеет определенного результата и вводит неопределенности и противоречия в математические выражения и уравнения. В то же время, существуют некоторые приближенные методы и понятия, которые позволяют изучать поведение функций и геометрических объектов вблизи нуля.

Вопрос-ответ:

Что произойдет, если разделить число на ноль в высшей математике?

Если разделить число на ноль в высшей математике, возникнет неопределенность. Исходя из математических правил, деление на ноль не определено, поэтому результат такой операции нельзя однозначно определить.

Почему нельзя разделить число на ноль в высшей математике?

Нельзя разделить число на ноль в высшей математике, потому что результатом такой операции является неопределенность. Математические правила запрещают деление на ноль, так как это противоречит логике и ломает основные принципы математики.

В чем заключается неопределенность при делении числа на ноль в высшей математике?

Неопределенность при делении числа на ноль в высшей математике заключается в том, что невозможно однозначно определить результат такой операции. Различные математические методы и теории дают разные результаты при делении на ноль, поэтому это считается неопределенной операцией.

Какие последствия могут быть при делении числа на ноль в высшей математике?

При делении числа на ноль в высшей математике могут возникнуть различные последствия, такие как неопределенность, ошибки в вычислениях, некорректные результаты. Это может привести к неверным выводам и искажению данных в математических моделях и расчетах.

Можно ли в высшей математике разделить число на ноль и получить конкретный результат?

Нет, нельзя в высшей математике разделить число на ноль и получить конкретный результат. Деление на ноль запрещено математическими правилами и противоречит основным принципам математики. Результатом такой операции будет неопределенность.

Можно ли разделить число на ноль в высшей математике?

Нет, нельзя разделить число на ноль в высшей математике. Деление на ноль является математической ошибкой и не имеет смысла. Результатом такого деления будет неопределенность или некорректность выражения.