Что такое алгоритм математика

Алгоритм математика — это последовательность шагов или инструкций, которые используются для решения математических задач. Эти алгоритмы могут быть простыми или сложными, и они играют важную роль в различных областях математики, таких как арифметика, геометрия и алгебра. Знание алгоритмов помогает математикам решать задачи более эффективно и систематически, а также является основой для разработки компьютерных программ и алгоритмического мышления. Изучение алгоритмов математики позволяет улучшить навыки логического мышления, анализа и решения проблем.

Алгоритм в математике – это последовательность точно определенных инструкций, которые следует выполнять для решения математической задачи. Алгоритмы – это основа работы компьютеров, а также могут использоваться для решения различных задач в нашей повседневной жизни.

Основная задача алгоритма – это решение задачи путем последовательного выполнения определенных действий. Алгоритмы могут быть представлены в виде блок-схем, псевдокода или программного кода. Они могут быть простыми или сложными, в зависимости от задачи, которую они решают.

Алгоритмы могут быть использованы в различных областях математики, таких как арифметика, алгебра, геометрия и т.д. Они помогают упорядочить и систематизировать наши действия при решении математических задач и делают процесс их решения более понятным и эффективным.

Примером алгоритма может служить алгоритм деления двух чисел. Сначала мы делим число, которое называется делимым, на число, которое называется делителем. Затем мы записываем результат деления, который называется частным. Если есть остаток от деления, мы также его записываем.

Алгоритм математика: определение и примеры

Основной компонент алгоритма — это инструкции, которые описывают, какие операции нужно выполнить и в какой последовательности. Каждая инструкция может быть выполнена за конечное количество шагов и дает определенный результат. Инструкции могут включать математические операции, логические условия, циклы и другие конструкции, позволяющие организовать выполнение задачи.

Примером алгоритма в математике может быть решение уравнения. Например, для решения уравнения «2x + 3 = 7» можно использовать следующие инструкции:

1. Вычесть 3 из обеих частей уравнения: «2x = 4»
2. Разделить обе части на 2: «x = 2»

Эти инструкции позволяют найти значение переменной x, при котором уравнение будет выполняться. Такой алгоритм можно применять для решения любого уравнения с одной переменной.

Алгоритмы также широко используются для вычисления математических функций, построения графиков и других задач. Они позволяют автоматизировать рутинные операции и упрощают работу с математическими задачами.

Видео по теме:

Что такое алгоритм в математике?

Алгоритмы в математике широко применяются для решения различных задач, таких как нахождение корней уравнений, вычисление суммы чисел, построение графиков функций и т.д. Они могут быть простыми и состоять из нескольких шагов или сложными, требующими выполнения большого количества операций.

Примером алгоритма в математике может служить алгоритм Евклида для нахождения наибольшего общего делителя двух чисел. Он состоит из следующих шагов:

ШагОписание

1	Начать с двух заданных чисел
2	Проверить, равны ли заданные числа
3	Если числа равны, то это и есть наибольший общий делитель
4	Если числа не равны, то заменить большее число разностью между ними
5	Повторить шаги 2-4, пока числа не станут равными
6	Наибольший общий делитель найден

Таким образом, алгоритмы в математике позволяют систематизировать процесс решения задачи и сделать его более понятным и эффективным.

Основные элементы алгоритма

ЭлементОписание

Ввод данных	Этот элемент указывает на необходимость получения входных данных, которые понадобятся для работы алгоритма.
Вычисления	Этот элемент описывает операции, которые нужно выполнить над входными данными, чтобы получить требуемый результат.
Условия	Этот элемент определяет различные ситуации, которые могут возникнуть в процессе выполнения алгоритма, и указывает, какой шаг нужно выполнить в зависимости от условия.
Циклы	Этот элемент позволяет выполнять одну и ту же последовательность шагов несколько раз в зависимости от заданных условий.
Вывод данных	Этот элемент определяет, как результат работы алгоритма будет представлен пользователю или записан в выходной файл.

Комбинирование этих элементов позволяет создавать сложные алгоритмы, способные решать разнообразные математические задачи.

Вопрос-ответ:

Что такое алгоритм в математике?

Алгоритм в математике — это последовательность шагов, которую можно использовать для решения математической задачи. Он является формальным и точным описанием процесса решения задачи.

Какие примеры алгоритмов в математике?

Примеры алгоритмов в математике могут быть различными. Например, алгоритм для сложения двух чисел: 1) Вводятся два числа; 2) Складываются введенные числа; 3) Выводится результат сложения. Еще один пример — алгоритм для нахождения факториала числа: 1) Вводится число; 2) Инициализируется переменная для результата; 3) В цикле умножается результат на текущее число, уменьшая его на единицу на каждой итерации; 4) Выводится результат.

Какие свойства должен обладать алгоритм в математике?

Алгоритм в математике должен обладать следующими свойствами: 1) Корректность — он должен решать задачу правильно; 2) Определенность — каждый шаг алгоритма должен быть однозначно определен; 3) Конечность — алгоритм должен завершаться за конечное число шагов; 4) Входные и выходные данные — алгоритм должен иметь входные данные, на которых он будет работать, и выходные данные, которые он выдаст в результате своей работы.

Какие еще области применения алгоритмов в математике?

Алгоритмы в математике применяются не только для решения математических задач. Они также используются в компьютерной науке, криптографии, оптимизации, искусственном интеллекте, статистике и других областях. В компьютерной науке, например, алгоритмы используются для разработки программ, обработки данных и решения сложных задач.

Какие есть методы разработки алгоритмов в математике?

Существует несколько методов разработки алгоритмов в математике. Некоторые из них включают: 1) Жадный метод — выбор локально оптимальных решений на каждом шаге; 2) Динамическое программирование — разбиение задачи на подзадачи и нахождение оптимального решения для каждой подзадачи; 3) Разделяй и властвуй — разбиение задачи на несколько подзадач, решение каждой подзадачи отдельно и объединение решений; 4) Итеративное улучшение — постепенное улучшение решения на каждом шаге.

Как можно определить алгоритм в математике?

В математике алгоритм можно определить как точную последовательность шагов или инструкций, которые выполняются для решения определенной задачи или получения конкретного результата.

Примеры алгоритмов в математике

Алгоритмы в математике используются для решения различных задач и применяются в различных областях этой науки. Вот несколько примеров алгоритмов в математике:

1. Алгоритм Евклида для нахождения наибольшего общего делителя двух чисел. Данный алгоритм основывается на принципе деления с остатком и позволяет эффективно находить наибольший общий делитель двух чисел.
2. Алгоритм сортировки пузырьком. Этот алгоритм используется для упорядочивания элементов в массиве. Он последовательно сравнивает пары соседних элементов и меняет их местами, если они находятся в неправильном порядке, до тех пор, пока массив не будет отсортирован.
3. Алгоритм быстрого возведения в степень. Данный алгоритм позволяет быстро возводить число в заданную степень. Он основан на раскладывании степени на двоичную систему и применении свойства четности/нечетности степени.
4. Метод Гаусса для решения систем линейных уравнений. Этот алгоритм позволяет находить решение системы линейных уравнений путем преобразования исходной системы к эквивалентной системе, в которой каждое уравнение имеет только одну неизвестную.
5. Алгоритм поиска кратчайшего пути в графе. Данный алгоритм используется для нахождения кратчайшего пути между двумя вершинами в графе. Он основан на обходе графа и обновлении расстояний до вершин на каждом шаге.

Это лишь некоторые примеры алгоритмов в математике. Все они служат инструментами для решения различных математических задач и играют важную роль в исследовании и развитии этой науки.

Как работает алгоритм в математике?

1. Определение и формулировка задачи. В этом этапе необходимо понять, что именно требуется решить и каковы условия задачи.
2. Разработка плана решения. В этом этапе определяются шаги, которые необходимо выполнить для решения задачи.
3. Выполнение шагов плана. Здесь каждый шаг плана решения последовательно выполняется с помощью математических операций и алгоритмов.
4. Анализ полученных результатов. В этом этапе проверяется правильность решения задачи и оценивается его точность.
5. Документирование решения. Результаты работы алгоритма фиксируются в виде записей, графиков или таблиц.

Каждый шаг алгоритма в математике должен быть четко определен и иметь ясную инструкцию для выполнения. Алгоритмы в математике используются для решения различных задач, таких как вычисление чисел, решение уравнений, построение графиков и т. д. Они помогают систематизировать и упростить процесс решения математических задач и повышают точность результатов.

Эффективность алгоритмов в математике

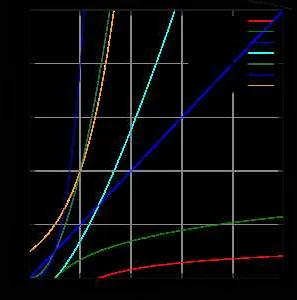
Одним из показателей эффективности алгоритма является его временная сложность. Временная сложность определяет, сколько времени требуется алгоритму для выполнения задачи в зависимости от размера входных данных. Чем меньше временная сложность, тем быстрее работает алгоритм.

Другим показателем эффективности алгоритма является его пространственная сложность. Пространственная сложность определяет, сколько памяти требуется алгоритму для выполнения задачи. Чем меньше пространственная сложность, тем меньше памяти занимает алгоритм.

Эффективность алгоритмов в математике может быть оценена при помощи технических анализов и экспериментов. Часто в математике используются асимптотические оценки, которые позволяют оценить эффективность алгоритма при больших размерах входных данных.

Примером эффективного алгоритма в математике является алгоритм Евклида для нахождения наибольшего общего делителя двух чисел. Этот алгоритм имеет временную сложность O(log(min(a, b))), где a и b — входные числа. Такая временная сложность позволяет алгоритму быстро работать даже для больших чисел.

Виды алгоритмов в математике

В математике существует множество различных видов алгоритмов, которые применяются для решения разнообразных задач. Рассмотрим некоторые из них:

1. Арифметические алгоритмы: это алгоритмы, которые используются для выполнения арифметических операций, таких как сложение, вычитание, умножение и деление. Например, алгоритм умножения двух чисел или алгоритм нахождения наибольшего общего делителя.
2. Алгоритмы сортировки: эти алгоритмы применяются для упорядочивания элементов в некотором наборе данных. Например, алгоритм сортировки пузырьком или алгоритм сортировки слиянием.
3. Алгоритмы поиска: эти алгоритмы используются для нахождения определенного элемента в некотором наборе данных. Например, алгоритм линейного поиска или алгоритм двоичного поиска.
4. Графовые алгоритмы: это алгоритмы, которые применяются для работы с графами — абстрактными структурами, состоящими из вершин и ребер. Например, алгоритм обхода графа в глубину или алгоритм нахождения кратчайшего пути в графе.
5. Алгоритмы оптимизации: эти алгоритмы используются для нахождения наилучших решений в определенных условиях. Например, алгоритм симплекс-метода или алгоритм генетического поиска.

Это только некоторые из видов алгоритмов, которые применяются в математике. Они помогают нам решать самые разные задачи и находить оптимальные решения.

Алгоритмы и компьютерная математика

Алгоритмы в компьютерной математике могут быть использованы для решения широкого спектра задач, включая численные методы, оптимизацию, символьные вычисления и многое другое. Они позволяют программистам и математикам разрабатывать эффективные и точные методы решения сложных математических проблем.

Примером алгоритма, используемого в компьютерной математике, может быть алгоритм Евклида для нахождения наибольшего общего делителя двух чисел. Этот алгоритм основан на простой итеративной процедуре, которая последовательно выполняет деление с остатком до тех пор, пока остаток не станет равным нулю. Результатом работы алгоритма является наибольший общий делитель исходных чисел.

Другим примером алгоритма, используемого в компьютерной математике, является алгоритм быстрого возведения в степень. Этот алгоритм позволяет эффективно вычислять степень числа, используя бинарное разложение показателя степени. Он основан на свойстве возведения числа в степень, которое позволяет уменьшить число умножений, требуемых для получения результата.

В компьютерной математике существует множество других алгоритмов, используемых для решения различных задач. Они могут быть разработаны как специально для конкретной задачи, так и быть общими и применяться для решения различных проблем. Основное требование к алгоритмам в компьютерной математике — это их эффективность и точность.

• Алгоритмы играют важную роль в компьютерной математике.
• Компьютерная математика — это область математики, в которой исследуются методы и алгоритмы, используемые для решения математических проблем с помощью компьютеров.
• Алгоритмы в компьютерной математике могут быть использованы для решения широкого спектра задач, включая численные методы, оптимизацию, символьные вычисления и многое другое.
• Примером алгоритма, используемого в компьютерной математике, может быть алгоритм Евклида для нахождения наибольшего общего делителя двух чисел.
• Другим примером алгоритма, используемого в компьютерной математике, является алгоритм быстрого возведения в степень.
• В компьютерной математике существует множество других алгоритмов, используемых для решения различных задач.
• Основное требование к алгоритмам в компьютерной математике — это их эффективность и точность.

Задачи, решаемые с помощью алгоритмов в математике

Алгоритмы играют важную роль в математике, позволяя решать различные задачи. Ниже представлены некоторые примеры задач, решаемых с помощью алгоритмов:

1. Решение уравнений: Алгоритмы могут быть использованы для решения различных типов уравнений, таких как линейные, квадратные или трансцендентные уравнения. Они позволяют найти все корни уравнения или найти приближенные значения корней.
2. Оптимизация функций: Алгоритмы оптимизации могут быть использованы для поиска экстремумов функций. Они позволяют найти максимумы или минимумы функций с использованием различных методов, таких как метод Ньютона или метод градиентного спуска.
3. Нахождение простых чисел: Алгоритмы нахождения простых чисел позволяют определить, является ли число простым или составным. Такие алгоритмы могут использоваться, например, при проверке чисел на простоту или при генерации больших простых чисел для криптографических целей.
4. Решение задач комбинаторики: Алгоритмы комбинаторики позволяют решать задачи, связанные с перестановками, сочетаниями, разбиениями и другими комбинаторными структурами. Они могут использоваться, например, для нахождения числа способов размещения объектов или для решения задачи о рюкзаке.
5. Решение задач графовой теории: Алгоритмы графовой теории позволяют решать задачи, связанные с поиском кратчайшего пути в графе, определением связности графа, нахождением минимального остовного дерева и другими. Они находят применение в различных областях, таких как логистика, транспортные сети и социальные сети.

Это лишь некоторые примеры задач, которые можно решить с помощью алгоритмов в математике. Алгоритмы являются мощным инструментом для решения различных математических задач и широко применяются в научных и практических исследованиях.