Что такое гл в математике

Гл в математике – это обозначение для группы, которая обладает особыми свойствами и операциями. Узнайте, что такое гл, какие его характеристики и применение в математике.

В математике гл — это сокращение от «группа линейных преобразований». Группа линейных преобразований — это множество всех возможных преобразований векторного пространства, сохраняющих операцию сложения векторов и умножение на число. Главной чертой группы линейных преобразований является то, что она обладает замкнутостью относительно операций сложения и композиции.

Группа линейных преобразований имеет несколько ключевых свойств. Во-первых, в ней обязательно присутствует нейтральный элемент, который не меняет положение вектора при преобразовании. Во-вторых, каждый элемент группы обладает обратным элементом, то есть для каждого преобразования существует обратное к нему преобразование, которое отменяет его действие. В-третьих, композиция двух преобразований из группы также является преобразованием из этой группы.

Примером гл в математике может служить группа поворотов на плоскости. Эта группа состоит из всех возможных поворотов на угол, кратный некоторому фиксированному углу. При этом выполняются все основные свойства группы линейных преобразований: нейтральным элементом является нулевой поворот (поворот на 0 градусов), для каждого поворота существует обратный поворот и композиция двух поворотов также является поворотом.

Группы линейных преобразований широко применяются в математике и физике. Они играют важную роль в линейной алгебре, геометрии, теории вероятностей и других областях. Изучение групп линейных преобразований позволяет более глубоко понять структуру и свойства векторных пространств и решать разнообразные задачи, связанные с преобразованиями и симметриями.

Определение гл в математике

Основные свойства гл:

1. Закон замкнутости — результат операции над элементами гл также является элементом этого гла.
2. Ассоциативность — результат операции не зависит от порядка, в котором производится операция.
3. Существование нейтрального элемента — существует элемент гла, при операции с которым другие элементы не изменяются.
4. Существование обратного элемента — к каждому элементу гла существует обратный элемент, при операции с которым результат равен нейтральному элементу.

Примеры гл:

• Множество целых чисел со сложением является глом.
• Множество вещественных чисел со сложением является глом.
• Множество обратимых матриц размером n×n с операцией умножения является глом.

Глы являются важным инструментом в алгебре и находят применение в различных областях математики и физики.

Видео по теме:

Примеры гл в математике

Гл в математике представляет собой функцию, которая принимает на вход некоторое множество и возвращает его наибольший элемент.

Пример 1:

Множество AГл(A)

{1, 2, 3}	3
{-10, 0, 10}	10
{-5, -3, -1, 0, 1, 3, 5}	5

Пример 2:

Множество BГл(B)

{4, 7, 2, 9}	9
{-10, -7, -2, -9}	-2
{10}	10

Таким образом, гл функция может использоваться для определения наибольшего элемента в заданном множестве.

Свойства гл в математике

1. Закон коммутативности: Для любых двух чисел a и b выполняется равенство гл(a, b) = гл(b, a). Это означает, что порядок чисел, передаваемых в функцию гл, не влияет на ее результат.

2. Закон ассоциативности: Для любых трех чисел a, b и c выполняется равенство гл(гл(a, b), c) = гл(a, гл(b, c)). Это означает, что результат гл не зависит от того, в каком порядке применять функцию гл к нескольким числам.

3. Идемпотентность: Для любого числа a выполняется равенство гл(a, a) = a. Это означает, что если числа, передаваемые в функцию гл, одинаковы, то результатом будет это число само.

4. Нейтральный элемент: Существует такое число e, что для любого числа a выполняется равенство гл(a, e) = a и гл(e, a) = a. Это число называется нейтральным элементом относительно функции гл.

5. Функция гл может быть расширена на множество всех чисел, включая отрицательные числа и дроби, с сохранением своих основных свойств.

Применение гл в математике

Применение гл в математике широко распространено и находит применение во многих областях, включая алгебру, геометрию, анализ и теорию чисел.

В алгебре гл используется для определения структурных операций в различных алгебраических системах. Например, в групповой теории гл используется для определения операции группы, которая обладает свойством ассоциативности и наличием нейтрального элемента. В полугруппах и моноидах также применяется гл для определения операций, обладающих только свойством ассоциативности.

В геометрии гл используется для определения операций над точками, векторами и другими геометрическими объектами. Например, векторное сложение и умножение на скаляр являются примерами гл в геометрии.

В анализе гл применяется для определения операций над функциями и последовательностями. Например, сложение функций и умножение на число являются примерами гл в анализе.

В теории чисел гл применяется для определения операций над числами. Например, сложение и умножение являются примерами гл в теории чисел.

Таким образом, гл является основной операцией в математике и находит широкое применение в различных областях.

Гл и другие математические понятия

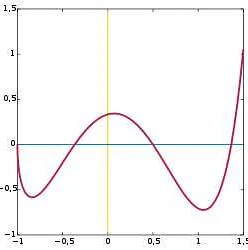
Гл (от англ. «glue») — это комбинаторное понятие, которое используется для описания соединения двух структур. Обычно гл применяется для объединения двух графов или двух циклов, но его можно использовать и для других структур.

Определение гл может быть следующим: для двух графов G1 и G2 гл G1#G2 — это граф, полученный путем соединения всех вершин из G1 со всеми вершинами из G2.

Например, если у нас есть граф G1 с вершинами A, B и граф G2 с вершинами C, D, то гл G1#G2 будет содержать вершины A, B, C, D и все возможные ребра между ними.

Гл можно использовать для решения различных задач, таких как поиск кратчайшего пути между двумя вершинами в соединенном графе, или поиск минимального остовного дерева в графе.

Кроме гла, в математике существуют и другие комбинаторные понятия, такие как операция объединения, пересечения, разности и декартово произведение множеств. Они позволяют нам комбинировать и анализировать различные множества и структуры.

ОперацияОписаниеПример

Объединение	Создает множество, содержащее все элементы из двух множеств.	{1, 2} ∪ {2, 3} = {1, 2, 3}
Пересечение	Создает множество, содержащее только элементы, присутствующие в обоих множествах.	{1, 2} ∩ {2, 3} = {2}
Разность	Создает множество, содержащее элементы из первого множества, не присутствующие во втором множестве.	{1, 2} \ {2, 3} = {1}
Декартово произведение	Создает множество, содержащее все возможные упорядоченные пары элементов из двух множеств.	{1, 2} × {3, 4} = {(1, 3), (1, 4), (2, 3), (2, 4)}

Эти математические понятия помогают нам разбираться в сложных структурах и решать различные задачи. Изучение гла и других комбинаторных понятий является важным шагом в понимании и применении математики в реальных ситуациях.

Связь гл с другими областями науки

Гл в математике имеет широкую связь с другими областями науки, такими как физика, экономика, биология и компьютерные науки.

В физике гл используется для описания законов и явлений природы. Например, при изучении движения частиц в пространстве и времени применяются гловые функции, которые описывают изменение показателей таких как скорость, ускорение и сила.

В экономике гл применяется для моделирования и анализа экономических процессов. Например, гловые модели используются для прогнозирования спроса и предложения на рынке, определения оптимальных стратегий инвестирования и оптимизации бизнес-процессов.

В биологии гл используется для изучения различных процессов в организмах и популяциях. Например, гловые модели применяются для изучения динамики популяции животных, моделирования генетических процессов и прогнозирования эволюционных изменений.

В компьютерных науках гл применяется для разработки алгоритмов, обработки данных и искусственного интеллекта. Например, гловые функции используются для обработки изображений, алгоритмов сжатия данных и машинного обучения.

Значение гл в решении задач

Гл (главное линейное) в математике используется для решения различных задач, особенно в области оптимизации и линейного программирования. Значение гл состоит в том, что он позволяет найти оптимальное решение задачи с учетом ограничений и целевой функции.

Гл используется для нахождения точек пересечения границ ограничений, которые определяют допустимое множество решений. Поэтому гл является важным понятием в решении задач на оптимизацию.

Примером использования гл может быть задача о максимизации прибыли предприятия. В этой задаче гл будет соответствовать значению, которое дает максимальную прибыль при заданных ограничениях на производство и продажу товаров.

ПеременнаяГраницы

Количество продукта 1	0 ≤ x1 ≤ 100
Количество продукта 2	0 ≤ x2 ≤ 200

Целевая функция, которую нужно максимизировать, может быть задана следующим образом:

f(x) = 3×1 + 5×2

Где x1 и x2 — количество продукта 1 и продукта 2 соответственно. Гл в этой задаче будет соответствовать значению x1 и x2, которые дадут максимальное значение функции f(x) при учете ограничений.

Вопрос-ответ:

Что такое гл в математике?

Гл — это сокращение от слова «группа». В математике группа — это алгебраическая структура, состоящая из множества и операции, обладающей определенными свойствами.

Какие свойства обладает группа?

Группа должна удовлетворять трем основным свойствам: замкнутости, ассоциативности и наличию обратного элемента.

Можете привести примеры групп?

Конечные группы: группа целых чисел по сложению, группа кватернионов, группа перестановок. Бесконечные группы: группа вещественных чисел по сложению, группа обратимых матриц.

Какие операции можно выполнять с элементами группы?

В группе можно выполнять операцию комбинирования — умножение элементов, операцию взятия обратного элемента, операцию взятия единичного элемента.

Какова роль групп в математике?

Группы являются основой для изучения других алгебраических структур, таких как кольца, поля, модули. Они также используются в различных областях математики и физики для решения разнообразных задач.

Как определить гл в математике?

В математике гл — это сокращение от гамма-функция. Гамма-функция — это специальная функция, которая обобщает понятие факториала на комплексные и действительные числа.

Можете привести пример использования гл в математике?

Конечно! Например, гл функция может использоваться для решения интегралов и уравнений в математическом анализе, а также для работы с комбинаторикой и теорией вероятностей.