Эвклидова математика и ее основные принципы: что это и какое значение имеет для современной науки

Эвклидова математика – это раздел геометрии, который изучает свойства и отношения прямых, углов, отрезков и плоскостей в двух- и трехмерном пространстве. В ее основе лежит аксиоматический метод, который сводит геометрию к формальной системе аксиом и логических выводов. Помимо геометрии, Эвклидова математика также включает в себя алгебру и теорию чисел.

Эвклидова математика — это классическая математика, основанная на работах древнегреческого математика Эвклида, который жил в 3 веке до нашей эры. Основные принципы этой математики до сих пор широко используются в науке, инженерии и технологиях.

Основная идея эвклидовой математики заключается в пространстве. Она исследует отношения между объектами в пространстве, а также приводит к пониманию, как изменения в одном объекте могут воздействовать на другие объекты.

Большинство математических теорий, связанных с геометрией, физикой и динамикой, базируются на принципах эвклидовой математики. Эта математика используется для описания движения твердых тел, распределения нагрузки или жидкости, а также для предсказания погоды и процессов, происходящих в космосе.

Необходимость изучать эвклидову математику становится понятной, когда осознаешь, насколько она важна для проведения научных исследований и создания новых технологий. Научиться понимать эвклидову математику может быть сложно, но это стоит усилий. Изучение ее принципов может привести к новым открытиям и решениям.

История возникновения эвклидовой математики

Эвклидова математика возникла в древней Греции в III веке до нашей эры. Ее создателем является древнегреческий математик Эвклид, который написал знаменитое произведение «Начала» (или «Элементы»), содержащее обширный материал о геометрии и арифметике.

«Начала» стали каноническим трудом эвклидовой математики и были тщательно изучены рядом выдающихся математиков и ученых, среди которых были Теон, Папп, Арабские геометры и др.

Эвклид учился на Александрийской школе, где получил образование в сфере философии, риторики, музыки, геометрии и астрономии. Его труды имели огромное значение для математики и философии в древности и стали основой для развития математического мышления и геометрии.

Сегодняшняя эвклидова геометрия базируется на постулатах, сформулированных Эвклидом в «Началах». В этих постулатах содержится ряд базовых утверждений, на которых базируется вся геометрия Эвклида. Также эвклидова математика имеет большое значение для современной науки, включая физику и информатику.

Видео по теме:

Определение понятий в эвклидовой геометрии

Эвклидова геометрия — это раздел математики, изучающий свойства пространства, основываясь на аксиомах, сформулированных древнегреческим математиком Эвклидом.

Пространство в эвклидовой геометрии описывается тремя измерениями длины, ширины и высоты. Измерения этих величин происходят независимо друг от друга и не влияют на изменение других измерений.

Прямая — это линия, которая не имеет ни начала, ни конца, и представляет собой наименьшее расстояние между двумя точками.

Угол в эвклидовой геометрии производится при соединении двух отрезков, которые начинаются от одной и той же точки. Угол может быть как острым, так и тупым, а также прямым, равным 90 градусов.

• Круг — это геометрическая фигура, определяемая точкой, называемой центром, и отрезком, называемым радиусом.
• Треугольник — это фигура, состоящая из трех отрезков, называемых сторонами, и трех углов, образованных этими сторонами.
• Четырехугольник — это геометрическая фигура, имеющая четыре стороны и четыре угла.

В эвклидовой геометрии используются также понятия параллельности, перпендикулярности, симметрии, и преобразований.

Аксиомы эвклидовой геометрии

Эвклидова геометрия является основной моделью геометрии, которая используется в нашей повседневной жизни. Эта геометрия основана на 5 базовых аксиомах, каждая из которых является предпосылкой для следующих построений и выводов:

1. Аксиома 1: Две точки могут быть соединены прямой.
2. Аксиома 2: Любая прямая может быть продолжена бесконечно в одном направлении.
3. Аксиома 3: Циркуль и линейка достаточны для построения любой фигуры.
4. Аксиома 4: Все прямые углы равны между собой.
5. Аксиома 5: Если прямая пересекает две другие прямые, то сумма внутренних углов на одной стороне меньше, чем два прямых угла.

Эти аксиомы вместе образуют базис для всех доказательств и построений в эвклидовой геометрии. Они ограничивают, что мы можем строить и как мы можем с ними работать, но в то же время, они позволяют делать некоторые фундаментальные выводы о геометрии нашего мира.

Соотношение эвклидовой и неевклидовой геометрии

Эвклидова геометрия основана на аксиомах Евклида, в которых описываются свойства пространства, которые мы знаем со школьной скамьи: прямые линии бесконечны, две прямые линии не могут пересекаться более одного раза и т.д.

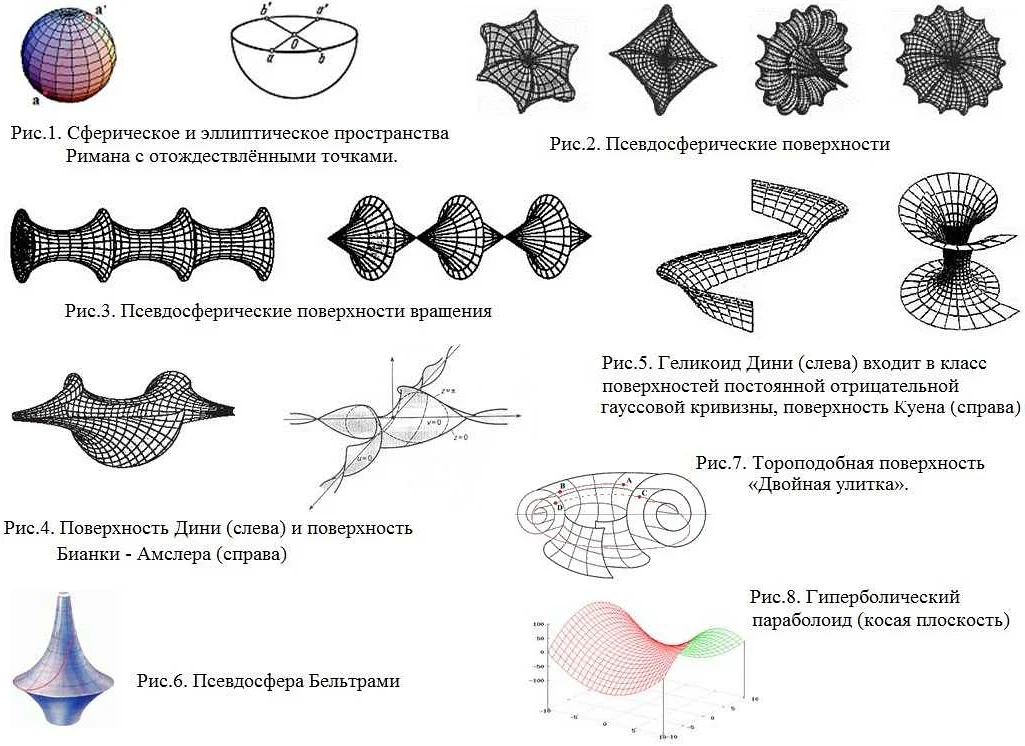
Однако, неевклидовы геометрии представляют собой различные математические теории, основанные на отказе от одной или нескольких аксиом Евклида, что приводит к интересным и неожиданным результатам. Например, гиперболическая геометрия отвергает аксиому о параллельности, и в данном пространстве существует неограниченное количество параллельных прямых, не пересекающих первоначальную прямую. А сферическая геометрия основывается на аксиоме о том, что на плоскости не существует прямой, проходящей через две заданные точки, что означает, что прямая, в данной геометрии, представляется как круговой луч.

Отказ от аксиом Евклида приводит к возможности создания множества несколько иных геометрий, в которых некоторые элементы пространства (прямые, углы и т.д.) имеют другие свойства. Именно по этой причине неевклидова геометрия считается более общей, чем эвклидова, и находит свое применение в различных областях знания.

Примеры задач в эвклидовой геометрии

Эвклидова геометрия – это математический подход, основанный на системе аксиом, которая определяет отношения между геометрическими объектами. Эти отношения могут быть использованы для решения различных геометрических задач. Рассмотрим несколько примеров:

• Задача о гипотенузе треугольника: Найдите длину гипотенузы прямоугольного треугольника, если известны длины катетов.
• Задача о касательной: Найдите уравнение касательной к окружности, заданной уравнением, в точке её пересечения с прямой.
• Задача о пересечении: Найдите координаты точки пересечения двух прямых, заданных уравнениями.
• Задача о подобии: Пусть два треугольника подобны. Найдите соотношение между их сторонами.

Решение этих задач основано на использовании различных аксиом эвклидовой геометрии, таких как аксиома параллельности, аксиома отношения и т.д. Кроме того, для решения задач может использоваться геометрический анализ, алгебра и другие математические методы.

Эвклидова геометрия является важной исторической разработкой в математике, которая оказала влияние на развитие геометрических понятий и методов. Благодаря ей возможно решение многих задач не только в геометрии, но и в других областях науки и техники.

Решение задач на основе аксиом эвклидовой геометрии

Эвклидова геометрия, основанная на пяти аксиомах, является наиболее распространенным типом геометрии, который используется в нашей повседневной жизни. Её аксиомы лежат в основе всех пространственных рассуждений и позволяют легко решать задачи на плоскости и в пространстве.

Процесс решения геометрической задачи начинается с понимания её формулировки и приведения её к определённому виду. Затем на основе аксиом эвклидовой геометрии, мы можем сформулировать начальные предположения и определить известные параметры. Затем, используя логику и применяя математические методы, мы можем вывести новые свойства и решить задачу.

Чтобы решить задачу на основе аксиом эвклидовой геометрии, нужно помнить о том, что эти аксиомы являются исходными постулатами, которые не могут быть доказаны. Поэтому, мы должны перейти от данных исходностей, к новым утверждениям, основываясь на уже известных свойствах и знаниях.

При решении задачи, мы также можем использовать геометрические построения и рисунки для упрощения интерпретации пространственных отношений и процесса решения.

Наконец, для проверки правильности решения задачи, мы можем сравнить результат с изначальными условиями и удостовериться в его соответствии.

В целом, решение задач на основе аксиом эвклидовой геометрии требует от нас логического мышления, понимания основных принципов геометрии и применения математических методов для вывода новых свойств и решения сложных задач.

Понятие пространства в эвклидовой математике

В эвклидовой математике пространством называется множество точек, которые могут быть описаны с помощью координатных систем. Пространство имеет определенную размерность, которая определяется количеством координат, необходимых для описания точки в этом пространстве.

Эвклидово пространство называется таким в честь греческого математика Евклида, который первым изучал свойства геометрических фигур в трехмерном пространстве. В эвклидовом пространстве применяются правила и геометрические законы, которые позволяют определить расстояние между точками и угол между векторами.

В эвклидовой математике существует два основных типа пространств: пространство векторов и пространство точек. Пространство векторов состоит из упорядоченного набора векторов, каждый из которых имеет определенный направление и длину. Пространство точек представляет собой множество точек, каждая из которых имеет свои координаты в пространстве.

• Примеры пространств в эвклидовой математике:
• Двумерное пространство – плоскость;
• Трехмерное пространство – объемный простор;
• Пространство векторов – например, линейное пространство;
• Пространство точек – например, геометрическое пространство.

Каждое пространство в эвклидовой математике имеет свои особые свойства и применения. Они используются в математике, науке, технике и других областях для решения различных задач и проблем.

Свойства и примеры пространств Евклида

Симметрия

Пространство Евклида симметрично относительно нулевой точки. Это означает, что если мы возьмем любой вектор и заменим его на противоположный, то длина и направление вектора останутся неизменными, а только его конечная точка изменится.

Пирсонова корреляция

Пирсонова корреляция — это мера того, насколько два вектора связаны друг с другом. Она используется для измерения качества описания данных линейной функцией, а также для оценки степени схожести или различия двух наборов данных.

Примеры пространств Евклида

• Геометрия плоскости — самый простой пример Евклидова пространства, состоящего из двух измерений.
• Геометрия трехмерного пространства — пример, в котором векторы имеют три измерения.
• Пространство функций — пример пространства, в котором векторами являются функции, а скалярным произведением является интеграл.
• Комплексное пространство — это Евклидово пространство с использованием комплексных чисел для описания координат.

Ортогональность и линейная независимость

В Евклидовом пространстве векторы называются ортогональными, если их скалярное произведение равно 0. Два вектора, которые не могут быть представлены как линейная комбинация, называются линейно независимыми. Линейная зависимость векторов означает, что один из векторов может быть выражен через линейную комбинацию других векторов.

Проективная геометрия и ее отношение к эвклидовой геометрии

Проективная геометрия — это раздел математики, который изучает свойства множества всех прямых в пространстве. Она рассматривает проективные преобразования и проективные пространства, которые являются обобщением понятия евклидова пространства.

В отличие от евклидовой геометрии, проективная геометрия не имеет понятия расстояния и угла. Вместо этого используется понятие проективных отношений. Однако, проективная геометрия связана с евклидовой геометрией, так как ее пространство может рассматриваться как пространство евклидовых прямых.

Проективная геометрия имеет большое значение в математике и физике. Например, она используется в проективной геометрии компьютерного зрения, в компьютерной графике, в теории кривых и поверхностей. Она также используется в теории относительности, где пространство рассматривается как проективное пространство.

В заключение, проективная геометрия представляет собой важный раздел математики, который находится в тесной связи с евклидовой геометрией и имеет множество приложений в различных областях науки.

Применение эвклидовой математики в физике и других отраслях

Эвклидова геометрия является основой многих научных дисциплин, включая физику. В физике она применяется для изучения пространственной структуры, распределения зарядов и других физических характеристик объектов.

Одним из примеров использования эвклидовой геометрии в физике является механика. Здесь используется понятие векторов, которые являются математическими объектами в трехмерном пространстве. Векторы используются для описания движения тел и распределения сил в пространстве.

Еще одним примером применения эвклидовой математики в физике является математическая физика. Этот раздел физики использует математические методы, основанные на эвклидовой геометрии, для решения различных задач и формулировки законов физики. Один из законов физики — закон Кулона — основан на принципах эвклидовой геометрии.

Эвклидова геометрия также нашла применение в других отраслях науки, таких как компьютерная графика и дизайн. В этих областях она используется для создания трехмерных моделей объектов, создания реалистичных изображений и анимаций.

Эвклидова математика также применяется в естественных науках, включая биологию и химию, где помогает описывать структуры молекул и организмов в трехмерном пространстве.

Также стоит упомянуть, что основанный на эвклидовой геометрии алгоритм Евклида используется для нахождения наибольшего общего делителя двух чисел, что имеет множество практических применений в криптографии, факторизации больших чисел и компьютерной алгебре.

Таким образом, эвклидова геометрия имеет множество практических применений в различных научных и технических областях, что подчеркивает ее важность и актуальность в современном мире.

Будущее эвклидовой математики и ее перспективы

Одним из главных направлений развития эвклидовой математики является расширение и дальнейшее развитие теории алгебраических структур. В частности, это связано с появлением и развитием новых математических объектов, таких как квадратичные формы, топологические пространства, алгебры Ли и др.

Также в последнее время особое внимание уделяется разработке компьютерных алгоритмов и программ, которые бы позволяли проводить различные вычисления и решать задачи в рамках эвклидовой математики. Это дает возможность использовать математические методы в таких областях, как информационные технологии, физика, химия и другие.

В дополнение к этому, эвклидова математика тесно связана с различными областями прикладной математики, такими как финансовая математика, статистика, теория управления и другие. Развитие этих областей также обеспечивает новые перспективы для эвклидовой математики в целом.

В целом, будущее эвклидовой математики обещает быть захватывающим и перспективным, так как она остается одной из основных областей математики, имеющих множество применений и открывающих новые возможности для научных и технологических исследований.

Вопрос-ответ:

Какие математические теории входят в эвклидову геометрию?

Эвклидова геометрия включает в себя теории прямых, плоскостей, углов, длин отрезков, треугольников, многоугольников, окружностей, сфер, векторного пространства и многого другого.

Какова история развития эвклидовой геометрии?

Эвклидова геометрия является одной из самых старых наук и развивалась на протяжении нескольких тысячелетий. Эвклидовое понимание геометрии выросло из египетской математики и было дополнено многими другими учеными, включая Аристотеля, Пифагора и Федривариуса. Самое полное и классическое изложение эвклидовой геометрии находится в «Элементах» Эвклида.

Как эвклидова геометрия связана с другими дисциплинами, такими как алгебра и анализ?

Хотя на первый взгляд эвклидова геометрия может показаться далекой от алгебры и анализа, на самом деле многие алгебраические и аналитические методы положены в основу этой дисциплины. Такие понятия, как координаты, уравнения и преобразования, широко используются в эвклидовой геометрии.

Какие основные принципы лежат в основе эвклидовой геометрии?

Основные принципы эвклидовой геометрии включают в себя аксиомы об отношениях между точками, линиями и плоскостями; аксиомы о расстоянии и углах; аксиомы о параллельных линиях; и аксиомы о пропорциях. Эти принципы образуют основу для всех доказательств в эвклидовой геометрии.

Какое значение имеет эвклидова геометрия в современном мире?

Эвклидова геометрия имеет большое значение в науке и технологии. Например, она используется в проектировании зданий, мостов и других инженерных сооружений, в разработке компьютерной графики и виртуальной реальности, в криптографии и многих других областях.

Что такое гипотеза Пуанкаре и как она связана с эвклидовой геометрией?

Гипотеза Пуанкаре — это одна из нерешенных задач математики, связанная с геометрией. Она утверждает, что каждая замкнутая трехмерная поверхность является трехмерной сферой, хотя такие поверхности могут иметь сложную топологию, которая не может быть представлена в трехмерном пространстве. Гипотеза Пуанкаре имеет прямое отношение к эвклидовой геометрии, так как она касается свойств трехмерного пространства.

Каковы применения эвклидовой геометрии в жизни?

Применения эвклидовой геометрии в жизни многовариантны. Единицы измерения многих объектов, например, длины, ширины, высоты дома или квадрата, представлены в эвклидовой форме. Кроме того, эвклидова геометрия используется в картографии, самолетостроении, машиностроении, компьютерной графике, судостроении и других областях практического применения.