Что такое математическая модель 5 класс

Математическая модель в 5 классе — это упрощенное представление реальной системы или явления с помощью математических символов и уравнений. Учебная статья рассказывает о том, как строить и использовать математические модели в пятом классе, чтобы решать различные задачи и понимать мир вокруг нас.

Математическая модель – это инструмент, который помогает нам лучше понять и описать различные явления и процессы с помощью математических выражений и формул. Она позволяет нам упростить сложные задачи и представить их в более понятной и структурированной форме.

Для учеников 5 класса понятие «математическая модель» может показаться сложным, но на самом деле оно очень простое. Например, представьте, что вам нужно посчитать площадь прямоугольника. Вместо того, чтобы измерять каждую сторону и умножать их вручную, вы можете использовать математическую модель, которая говорит нам, что площадь можно вычислить, умножив длину на ширину.

Математическая модель помогает нам не только решать задачи, но и предсказывать результаты и строить гипотезы. Она позволяет нам легче анализировать и объяснять различные явления в нашей жизни.

Примером математической модели может быть уравнение скорости, которое используется для описания движения предметов. Или уравнение роста растений, которое показывает, как растения растут со временем. Подобные модели помогают нам лучше понять и предсказать поведение различных объектов и явлений в нашей окружающей среде.

Что такое математическая модель?

Математическая модель состоит из математических символов и формул, которые описывают связи и зависимости между различными переменными. Она позволяет исследовать систему, проводить эксперименты и предсказывать ее поведение в разных условиях.

Примером математической модели может быть модель роста растения. В этом случае, переменные могут включать время, количество воды, уровень освещенности и другие факторы, которые влияют на рост растения. С помощью математических формул и уравнений можно определить, какие значения переменных приведут к оптимальному росту растения.

ПеременнаяОписание

Время	Количество времени, прошедшего с начала эксперимента
Вода	Количество воды, поданное на растение
Освещение	Уровень освещенности в комнате

В данном примере математическая модель может быть представлена уравнением: Рост = а * Вода + b * Освещение + c * Время, где а, b и c — коэффициенты, которые позволяют установить взаимосвязь между переменными и ростом растения.

Математические модели являются мощным инструментом для исследования и анализа сложных систем и помогают прогнозировать результаты. Они используются во многих областях науки и позволяют нам лучше понять и объяснить мир вокруг нас.

Определение и цель

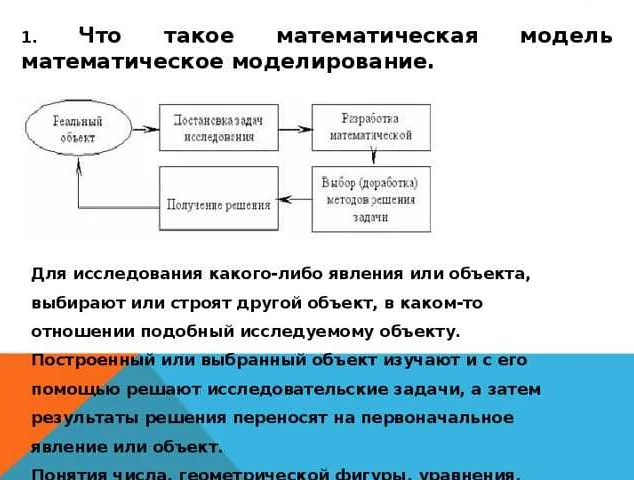
Цель математической моделирования в математике для 5 класса – это помочь учащимся лучше понять и применять математические понятия и методы на практике. Моделирование позволяет учащимся увидеть связь между математикой и реальным миром, а также развить навыки анализа, логического мышления и решения задач.

Принципы построения модели

При создании математической модели необходимо придерживаться нескольких принципов. Вот основные из них:

1. Упрощение реальности. Модель должна быть упрощенным отображением реального объекта, явления или процесса. Она должна существенно сокращать количество деталей и основных характеристик, чтобы быть понятной и удобной для исследования.

2. Выделение ключевых элементов. Важно определить основные переменные и параметры, которые будут использоваться в модели. Эти элементы должны быть наиболее существенными для понимания и исследования объекта моделирования.

3. Формализация. Модель должна быть представлена в формализованном виде, то есть с использованием математических символов и уравнений. Это позволяет проводить точные вычисления и получать количественные результаты.

4. Проверка и корректировка. Важно проверять модель на соответствие реальным данным и проводить корректировку, если необходимо. Это позволяет увеличить точность модели и достоверность ее результатов.

5. Интерпретация результатов. Полученные результаты моделирования должны быть интерпретированы и проанализированы с учетом контекста и целей работы. Важно понимать, какие выводы и рекомендации можно получить на основе моделирования.

Соблюдение этих принципов поможет построить адекватную и полезную математическую модель для изучения различных явлений и процессов.

Составляющие модели

Математическая модель состоит из нескольких основных составляющих:

Математические символы	Символы и знаки, которые используются для записи математических выражений и формул. Например, знаки «+», «-«, «*», «/» и т.д.
Переменные	Символы, которым присваиваются значения и которые могут изменяться. Например, «x» или «y».
Уравнения и неравенства	Математические выражения, которые связывают переменные и символы с помощью знаков равенства или неравенства. Например, «x + 2 = 5» или «y > 3».
Функции	Математические правила, которые связывают переменные и символы между собой. Например, функция «f(x) = x^2».
Задачи	Практические ситуации, которые требуют использования математической модели для решения. Например, задача о поиске площади прямоугольника.

Составляющие модели вместе позволяют описывать и анализировать различные явления и процессы в математике и других областях знаний.

Примеры математических моделей

Пример 1: Модель роста растения

Представим, что у нас есть растение, которое каждый день увеличивается на одну единицу. Мы можем создать математическую модель для описания его роста:

Рост = начальная высота + количество дней

Начальная высота и количество дней – это переменные, которые мы можем менять, чтобы предсказывать, какой будет высота растения через определенное количество дней.

Пример 2: Модель движения автомобиля

Представим, что мы хотим узнать, сколько времени займет путешествие на автомобиле с заданной скоростью и расстоянием. Мы можем использовать математическую модель для решения этой задачи:

Время = расстояние / скорость

Расстояние и скорость – это переменные, которые мы можем менять, чтобы предсказывать время путешествия.

Пример 3: Модель распределения населения

Представим, что мы хотим изучить изменение численности населения в городе на протяжении нескольких лет. Мы можем создать математическую модель для распределения населения:

Население = начальное население + (рождаемость — смертность) + (миграция — эмиграция)

Начальное население, рождаемость, смертность, миграция и эмиграция – это переменные, которые мы можем менять, чтобы предсказывать изменение численности населения.

Это лишь несколько примеров математических моделей. Математические модели важны в различных областях, таких как физика, экономика, биология и др. Они помогают нам лучше понять и предсказывать поведение объектов, систем и процессов в нашем мире.

Математическая модель в учебной программе

Математическая модель позволяет ученикам лучше понять и объяснить различные явления в окружающем мире с помощью математических методов. Она помогает выявить закономерности, предсказать результаты эксперимента и решить практические задачи.

Примеры математических моделей, которые изучаются в 5 классе, включают модели движения тела по прямой, модели сравнения и сложения дробей, модели работы с пропорциями и т.д. Ученики учатся работать с такими моделями, анализировать их, находить решения и делать выводы на основе математических законов и правил.

Изучение математических моделей помогает развить логическое мышление, абстрактное и аналитическое мышление, а также навыки применения математических методов для решения практических задач. Эти навыки пригодятся ученикам не только в школе, но и в жизни, где математика применяется во многих областях, включая науку, технологии, экономику и т.д.

Важно отметить, что математическая модель — это упрощенное описание реальности, которое не может учесть все факторы и детали. Однако она является полезным инструментом для изучения и понимания различных явлений и принятия решений на основе математических законов.

Зачем изучать математическую модель?

Изучение математической модели также помогает ученикам развивать навыки решения проблем, анализа ситуаций, построения гипотез и обоснования своих решений. Математическая модель позволяет представить сложные задачи и явления в виде простых математических выражений и формул, что упрощает их изучение и понимание.

Изучение математической модели также помогает развивать представление о взаимосвязях и зависимостях между различными явлениями и объектами. Это помогает ученикам лучше понимать мир вокруг них и применять математические знания в реальных ситуациях, например, в экономике, физике или социальных науках.

Таким образом, изучение математической модели является необходимым для развития математического мышления, логического мышления и аналитических способностей учеников, а также для их подготовки к решению сложных задач и анализу сложных ситуаций в различных областях знаний.

Роль математической модели в решении задач

Одной из главных преимуществ математической модели является возможность проведения различных экспериментов в виртуальной среде. Модель позволяет изменять параметры системы и оценивать их влияние на результаты. Это позволяет экономить время и ресурсы, которые могли бы потребоваться для проведения реальных экспериментов.

Кроме того, математическая модель помогает анализировать и предсказывать результаты сложных процессов или явлений. Она позволяет учесть все факторы, влияющие на систему, и оценить их взаимодействие. Таким образом, модель позволяет находить оптимальные решения, учитывая все ограничения и цели задачи.

Примером использования математической модели может служить задача о расчете пути движения автомобиля. Математическая модель будет учитывать такие факторы, как скорость движения, расстояние до цели, преграды на пути и другие параметры. С помощью модели можно определить оптимальную траекторию движения, время прибытия и прочие характеристики.

Таким образом, математическая модель является неотъемлемой частью решения задач в различных областях, от науки и техники до экономики и финансов. Она позволяет анализировать системы, прогнозировать результаты и находить оптимальные решения, что делает ее важным инструментом для практического применения математики.

Видео по теме:

Что такое математическая модель?

Математическая модель — это упрощенное описание некоторого явления или объекта с помощью математических символов и формул. Она позволяет анализировать и предсказывать поведение этого явления или объекта.

Для чего нужны математические модели?

Математические модели используются для решения различных задач и проблем в различных областях науки, техники и экономики. Они позволяют анализировать сложные системы, предсказывать их поведение, оптимизировать процессы и принимать решения на основе полученных результатов.

Какие навыки развиваются при работе с математическими моделями?

Работа с математическими моделями развивает навыки анализа, логического мышления, решения проблем, формулирования гипотез, представления данных в виде уравнений и графиков, интерпретации результатов, принятия решений на основе полученных данных. Это также помогает развить математическую интуицию и понимание связей между различными величинами.

Для чего нужна математическая модель?

Математическая модель используется для описания и анализа различных явлений и процессов в реальном мире. Она помогает упростить и абстрагировать сложные системы, чтобы понять их основные характеристики и взаимосвязи. Математическая модель позволяет предсказывать поведение объектов и принимать обоснованные решения на основе математических вычислений.