Что такое множество чисел в математике 3 класс
Содержимое
- 1 Что такое множество чисел в математике 3 класс
- 1.1 Определение множества чисел в математике
- 1.2 Множество натуральных чисел
- 1.3 Множество целых чисел
- 1.4 Множество рациональных чисел
- 1.5 Множество вещественных чисел
- 1.6 Множество иррациональных чисел
- 1.7 Видео по теме:
- 1.8 Вопрос-ответ:
- 1.9 Множество комплексных чисел
- 1.10 Примеры множеств чисел в математике для 3 класса
Множество чисел в математике для третьего класса — это набор различных чисел, которые могут быть упорядочены и использованы для решения задач и вычислений. В этой статье вы узнаете, как классифицировать числа, работать с ними и применять их в различных математических операциях.
Множество чисел — это набор чисел, которые имеют общие свойства или характеристики. В математике существуют различные виды множеств чисел, каждое из которых имеет свои особенности и правила. В 3 классе дети начинают изучать основные типы множеств чисел, которые помогут им в дальнейшем понимании и решении математических задач.
Одно из самых основных множеств чисел – это натуральные числа. Натуральные числа — это все положительные числа, начиная с единицы: 1, 2, 3, 4, 5 и так далее. Они используются для подсчета предметов, людей, дней и других объектов, которые можно перечислить.
Второе важное множество чисел для 3 класса – это целые числа. Целые числа — это натуральные числа, их противоположности (отрицательные числа) и нуль. Например: -3, -2, -1, 0, 1, 2, 3 и так далее. Целые числа используются для измерения температуры, глубины, долгов, координат и других величин, которые могут быть и отрицательными.
Третье множество чисел – это рациональные числа. Рациональные числа — это числа, которые можно представить в виде обыкновенной дроби. Например: 1/2, 3/4, -2/3, 5 и так далее. Рациональные числа используются для вычислений в финансовых задачах, объемах жидкостей, процентах и других ситуациях, где необходимо работать с дробными значениями.
Важно помнить, что каждое множество чисел имеет свои правила операций (сложение, вычитание, умножение, деление) и свои особенности. Изучение этих множеств поможет детям развить навыки логического мышления, а также улучшит их математическую грамотность.
Определение множества чисел в математике
Одно из основных множеств чисел – это множество натуральных чисел. В него входят все положительные целые числа, начиная с единицы. То есть, множество натуральных чисел можно представить следующим образом: {1, 2, 3, 4, 5, …}.
Также существует множество целых чисел, которое включает в себя все натуральные числа, а также их противоположные значения. То есть, множество целых чисел можно представить следующим образом: {…, -3, -2, -1, 0, 1, 2, 3, …}.
Еще одним множеством чисел является множество рациональных чисел. В него входят все числа, которые можно представить в виде обыкновенной или десятичной дроби. Например, числа 1/2, 3/4, 0.25 являются рациональными числами.
Существует также множество иррациональных чисел, которое включает в себя все числа, которые нельзя представить в виде дроби. Например, число π (пи) является иррациональным числом.
И, наконец, существует множество действительных чисел, которое объединяет в себе все рациональные и иррациональные числа. Множество действительных чисел обозначается символом ℝ.
Ознакомление с множествами чисел позволяет более глубоко изучить различные аспекты математики и использовать их в различных практических задачах.
Множество натуральных чисел
Множество натуральных чисел можно представить как бесконечную последовательность чисел:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …
Все числа в множестве натуральных чисел являются положительными и целыми, и они упорядочены по возрастанию. Множество натуральных чисел используется для обозначения количества объектов, позиций, дней и других естественных величин.
Множество целых чисел
Множество целых чисел в математике обозначается символом ℕ или Z и состоит из всех положительных и отрицательных чисел, а также нуля.
Другими словами, множество целых чисел включает в себя числа, которые можно представить без десятичных или дробных частей, а также все отрицательные числа и ноль.
Примеры целых чисел:
- −3
- −2
- −1
- 0
- 1
- 2
- 3
Множество целых чисел является бесконечным и несчетным, что означает, что его элементы нельзя пересчитать в последовательности.
Целые числа используются во многих областях математики, физики, программирования и других наук.
Множество рациональных чисел
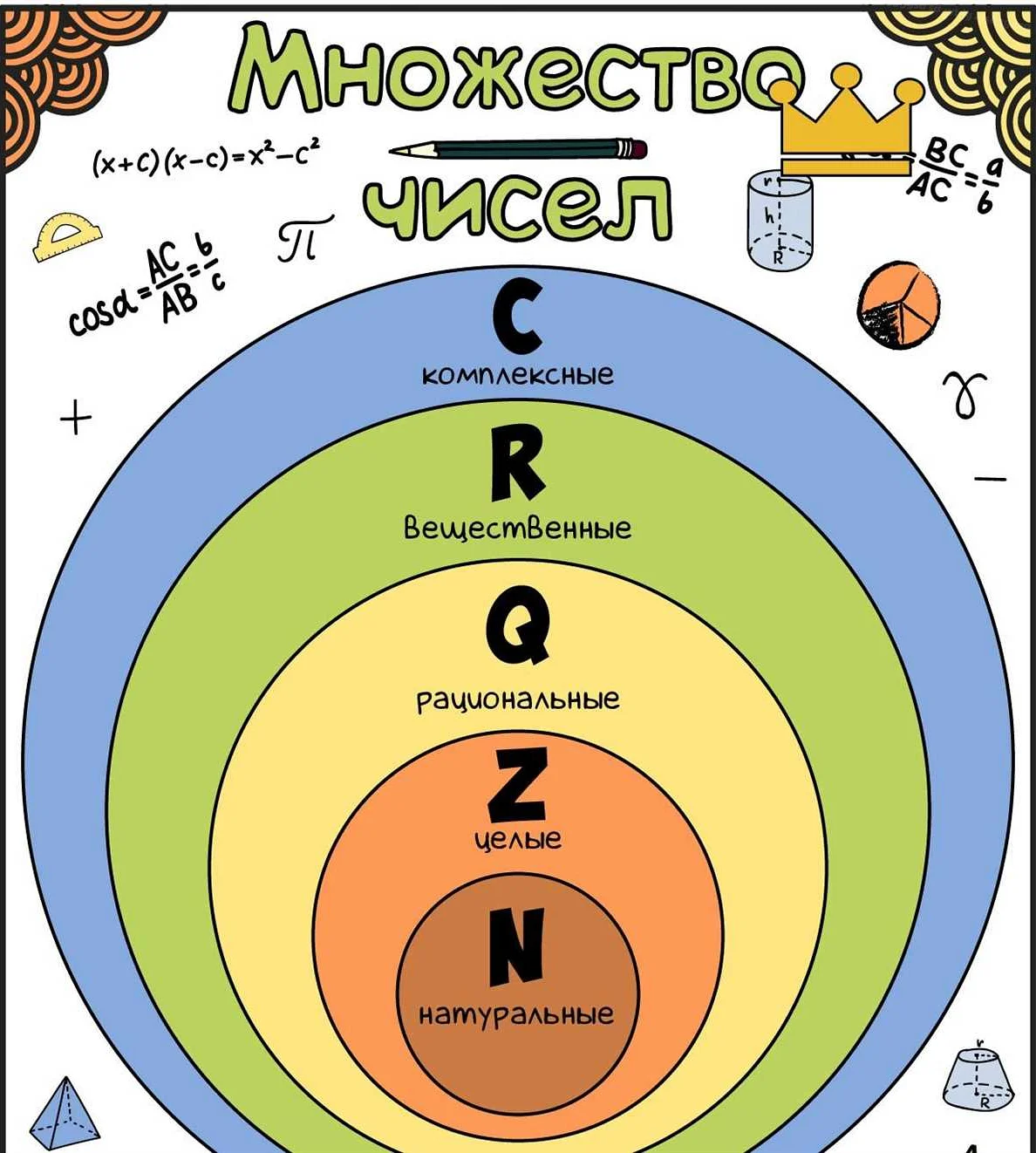
Рациональные числа можно записать в виде обыкновенной дроби a/b, где a — числитель и b — знаменатель. Оба числа являются целыми числами, и знаменатель не равен нулю.
Примеры рациональных чисел:
ЧислоЗапись
| 1 | 1/1 |
| -5 | -5/1 |
| 2/3 | 2/3 |
| -4/7 | -4/7 |
Множество рациональных чисел включает все обыкновенные и десятичные дроби, а также целые числа и нуль. Однако, множество рациональных чисел не включает числа, которые нельзя записать в виде дроби, например, корень из двух (√2) или число π (пи).
Множество вещественных чисел
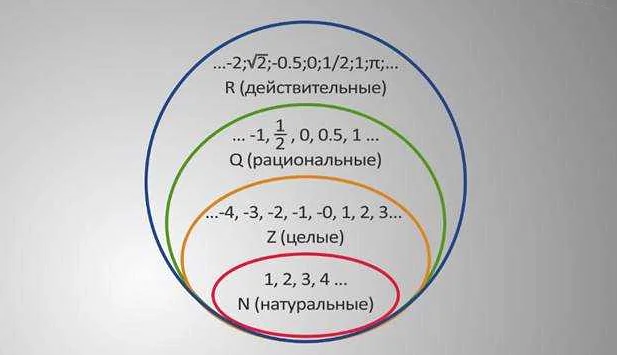
Вещественные числа можно представить на числовой прямой, где каждая точка на прямой соответствует определенному вещественному числу. Вещественные числа могут быть положительными, отрицательными или нулем.
Примеры вещественных чисел:
- −3
- 0
- 1.5
- −2.7
- √2
Важно помнить, что множество вещественных чисел является бесконечным и непрерывным.
Множество иррациональных чисел

В математике существуют два основных типа чисел: рациональные и иррациональные. Множество иррациональных чисел состоит из чисел, которые не могут быть выражены в виде обыкновенной дроби. Такие числа не могут быть представлены в виде десятичной дроби, которая заканчивается или повторяется.
Примером иррационального числа является число π (пи), которое равно отношению длины окружности к ее диаметру и приближенно равно 3,14159. Другим примером является число √2 (квадратный корень из 2), которое не может быть записано в виде обыкновенной дроби. Оно приближенно равно 1,41421.
Множество иррациональных чисел бесконечно и несчетно. Это означает, что их нельзя перечислить или поставить во взаимно однозначное соответствие с натуральными числами.
Примеры иррациональных чисел
| √2 |
| π |
| e (число Эйлера) |
| √3 |
| √5 |
Иррациональные числа играют важную роль в математике и используются во многих областях, включая физику, инженерию и информатику. Они расширяют наше понимание чисел и позволяют нам решать более сложные задачи.
Видео по теме:
Вопрос-ответ:
Что такое множество чисел?
Множество чисел в математике — это совокупность чисел, объединенных по определенному признаку или правилу. Например, множество натуральных чисел включает все положительные целые числа, начиная с единицы.
Какие примеры множеств чисел можно привести?
Примеры множеств чисел включают: множество натуральных чисел (1, 2, 3, …), множество целых чисел (-3, -2, -1, 0, 1, 2, 3, …), множество рациональных чисел (дроби вида a/b, где a и b — целые числа), множество действительных чисел (включает все рациональные и иррациональные числа) и так далее.
Какие числа входят в множество натуральных чисел?
Множество натуральных чисел включает все положительные целые числа, начиная с единицы. То есть, это числа 1, 2, 3, 4, 5, и так далее.
Какие числа входят в множество целых чисел?
Множество целых чисел включает все положительные и отрицательные целые числа, а также ноль. То есть, это числа …, -3, -2, -1, 0, 1, 2, 3, …
Множество комплексных чисел
Множество комплексных чисел образует плоскость, которая называется комплексной плоскостью. На комплексной плоскости точки соответствуют комплексным числам. Действительная часть комплексного числа соответствует координате по оси абсцисс, а мнимая часть – координате по оси ординат.
Комплексные числа можно складывать, вычитать, умножать и делить, применяя соответствующие правила. Например, сумма двух комплексных чисел a + bi и c + di равна (a + c) + (b + d)i. Умножение комплексных чисел определяется следующим образом: (a + bi) * (c + di) = (ac — bd) + (ad + bc)i.
Примером комплексного числа может служить число 2 + 3i. В этом случае 2 является действительной частью числа, а 3i – мнимой частью.
Примеры множеств чисел в математике для 3 класса
В математике для 3 класса существует несколько примеров множеств чисел, с которыми дети знакомятся на уроках:
1. Множество натуральных чисел
Множество натуральных чисел содержит все положительные числа, начиная с 1 и продолжая бесконечно: 1, 2, 3, 4, 5, и так далее.
2. Множество целых чисел
Множество целых чисел включает в себя натуральные числа, их противоположности (отрицательные числа) и ноль: …, -3, -2, -1, 0, 1, 2, 3, …
3. Множество рациональных чисел
Множество рациональных чисел состоит из всех чисел, которые можно представить в виде дроби, где числитель и знаменатель являются целыми числами и знаменатель не равен нулю. Например, 1/2, -3/4, 0/1 и т.д.
4. Множество десятичных дробей
Множество десятичных дробей включает в себя все числа, которые можно записать в виде конечной или бесконечной десятичной дроби. Например, 0.5, 1.25, 3.14159 и так далее.
5. Множество иррациональных чисел
Множество иррациональных чисел содержит все числа, которые невозможно представить в виде дроби. Примеры иррациональных чисел: корень квадратный из 2, число Пи (π), е и так далее.
Это лишь некоторые примеры множеств чисел, с которыми знакомятся дети в математике для 3 класса. Они помогают развивать понимание различных типов чисел и их свойств.
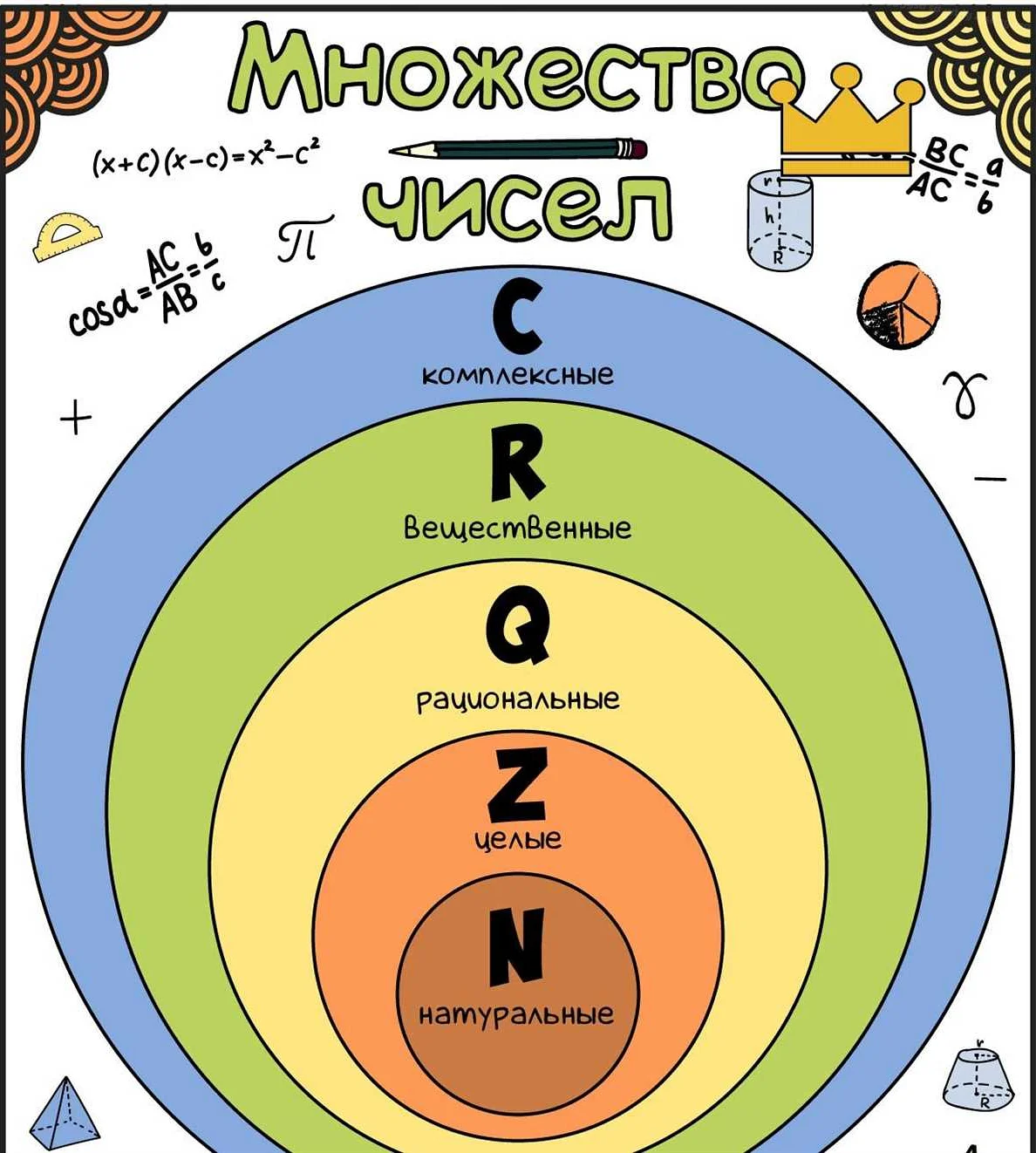



Статья очень понятно объясняет, что такое множество чисел в математике для учеников 3 класса. Я рад, что нашел эту информацию, так как теперь я понимаю, что множество чисел — это группа чисел, которые имеют общие характеристики. Например, множество четных чисел включает все числа, которые делятся на 2 без остатка. Также в статье приведены другие примеры множеств чисел, таких как множество нечетных чисел и множество простых чисел. Это помогает ученикам понять, что в математике существуют различные группы чисел, которые можно изучать и сравнивать. Я с нетерпением жду, чтобы поделиться этой информацией с моим ребенком, чтобы он мог лучше понять мир чисел и математику. В целом, статья очень полезная и информативная.
Множество чисел в математике для 3 класса — это основополагающая концепция, которая помогает детям понять и классифицировать числа в различные группы. Возможно, многие из нас помнят дни, когда мы только начинали изучать математику и понимали, что числа могут быть разными, но не всегда знали, как их организовать. Множество чисел — это набор уникальных чисел. Оно может включать в себя различные типы чисел, такие как натуральные, целые, рациональные и дробные числа. Каждое число в множестве отличается от других чисел и имеет свою уникальную характеристику. Например, множество натуральных чисел — это набор чисел, начиная с 1 и включающий все положительные целые числа без дробной части. Оно может включать числа 1, 2, 3, 4 и так далее. Дети учатся считать и распознавать натуральные числа, используя их знание об их порядке и последовательности. Другое примером множества чисел может быть множество четных чисел. В этом случае, множество будет включать все числа, которые делятся на 2 без остатка, такие как 2, 4, 6, 8 и так далее. Это помогает детям понять, что числа могут быть классифицированы на основе их уникальных свойств. Понимание множеств чисел позволяет детям развивать свои навыки счета, сравнения чисел, а также решения математических задач. Они могут использовать эти знания для сравнения чисел, нахождения наибольшего или наименьшего числа, а также для выполнения операций сложения и вычитания. В целом, понимание и использование множеств чисел в математике для 3 класса является важным шагом в их математическом развитии. Это помогает им лучше понять и организовать числа, что является фундаментом для решения более сложных задач в будущем.