Что такое объем 5 класс по математике

Объем 5 класс по математике – это раздел математики, который изучает понятие объема и его измерение. В этом разделе ученики узнают, как найти объем различных геометрических фигур, таких как параллелепипеды, призмы и цилиндры. Учебная программа включает в себя задачи на нахождение объема, а также упражнения по применению формул для его вычисления. Успешное освоение материала позволяет ученикам лучше понять трехмерную геометрию и развить навыки решения задач в этой области.

Объем — одно из основных понятий, изучаемых в 5 классе по математике. Он представляет собой меру трехмерного пространства, занимаемого телом. Понимание и умение работать с объемом являются важными навыками для решения различных задач и заданий.

Основные понятия, связанные с объемом, включают единицы измерения (кубические сантиметры, кубические метры и т.д.), а также методы вычисления объема для различных геометрических фигур, таких как параллелепипеды, призмы, цилиндры и шары. Знание формул и правил для вычисления объема позволяет ученикам решать задачи на нахождение объема тел и использовать его для решения других математических задач.

Например, в задаче на вычисление объема параллелепипеда ученик должен знать формулу: объем равен произведению длины на ширину на высоту. При решении задачи он должен уметь подставить соответствующие значения в формулу и выполнить вычисления.

Осознание и понимание понятия объема играют важную роль в развитии логического мышления и умения решать проблемы. Понятие объема также используется в других областях науки и техники, таких как архитектура, инженерия и геометрическое моделирование.

Основные понятия объема 5 класс

Геометрические фигуры – это объекты, которые можно описать с помощью геометрических понятий, таких как точка, прямая, плоскость.

Параллелепипед – это геометрическое тело, у которого противоположные грани параллельны и равны по форме.

Куб – это особый вид параллелепипеда, у которого все грани равны и прямоугольные.

Цилиндр – это геометрическое тело, у которого две основания являются параллельными кругами, а боковая поверхность – прямыми.

Пирамида – это геометрическое тело, у которого одно из оснований является многоугольником, а боковые грани – треугольниками.

Шар – это геометрическое тело, у которого все точки равноудалены от центра.

Поверхность тела – это граница фигуры, разделяющая фигуру и окружающее пространство.

Задача на определение объема – это задача, в которой требуется найти объем геометрического тела, используя заданные размеры.

Задача на нахождение размеров – это задача, в которой требуется найти размеры геометрического тела, используя заданный объем.

Задача на нахождение неизвестного объема – это задача, в которой требуется найти неизвестный объем геометрического тела, используя заданные размеры.

Видео по теме:

Определение объема

Для того чтобы определить объем тела, необходимо знать его форму и размеры. Обычно объем вычисляется с помощью формул. Например, для прямоугольного параллелепипеда объем можно вычислить по формуле:

Объем (V) =

Длина (l) ×

Ширина (w) ×

Высота (h)

Таким образом, чтобы найти объем прямоугольного параллелепипеда, необходимо перемножить его длину, ширину и высоту.

Определение объема позволяет решать различные задачи, связанные с измерением и оценкой объема предметов и тел.

Формула для вычисления объема

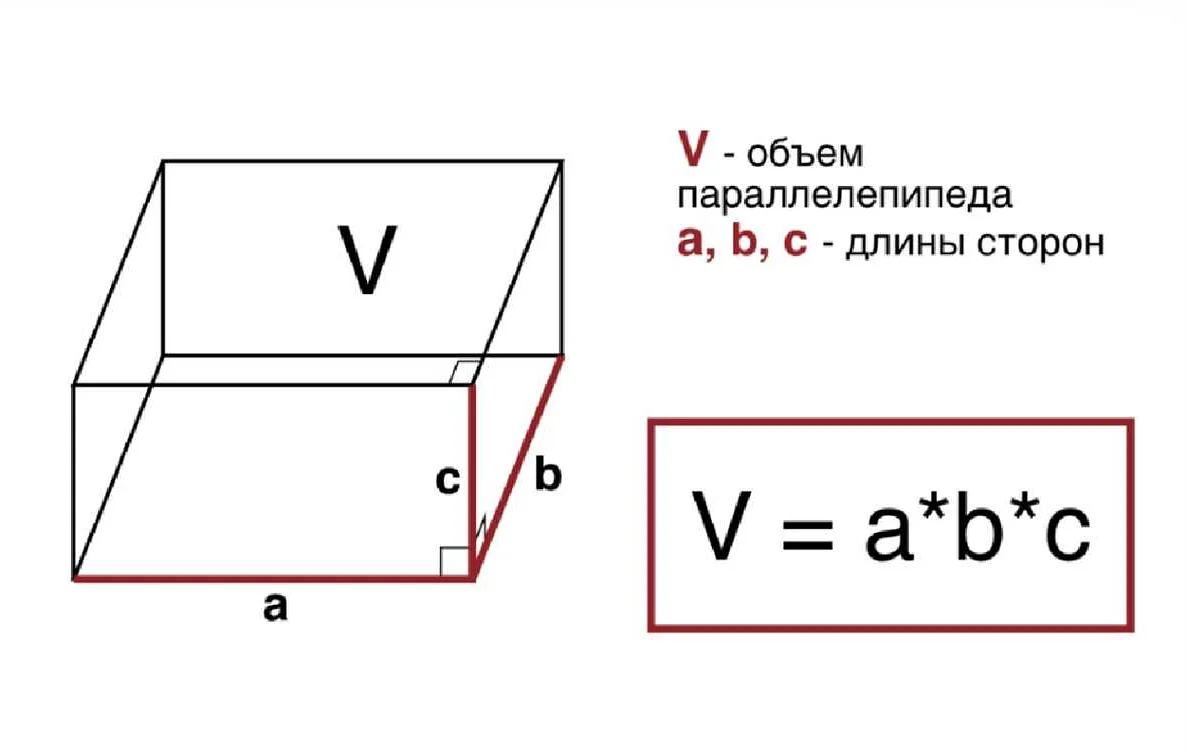
Формула для вычисления объема прямоугольного параллелепипеда:

• Объем (V) = Длина (a) × Ширина (b) × Высота (h)

Формула для вычисления объема куба (прямоугольного параллелепипеда, у которого все ребра равны):

• Объем (V) = Длина ребра (a) × Длина ребра (a) × Длина ребра (a)

Формула для вычисления объема цилиндра:

• Объем (V) = Площадь основания (S) × Высота (h)

Формула для вычисления объема шара:

• Объем (V) = (4/3) × Пи (π) × Радиус (r) × Радиус (r) × Радиус (r)

Формула для вычисления объема пирамиды:

• Объем (V) = (Площадь основания (S) × Высота (h)) / 3

Зная формулы для вычисления объема различных фигур, можно приступать к решению задач, в которых необходимо найти объем. Для этого нужно знать значения соответствующих сторон или параметров фигуры и подставить их в соответствующую формулу.

Единицы измерения объема

Наиболее распространенными единицами измерения объема являются:

• Кубический миллиметр (мм3) — обозначается мм3. Это объем, занимаемый кубом со стороной длиной 1 миллиметр.
• Кубический сантиметр (см3) — обозначается см3. Это объем, занимаемый кубом со стороной длиной 1 сантиметр.
• Кубический дециметр (дм3) — обозначается дм3. Это объем, занимаемый кубом со стороной длиной 1 дециметр.
• Литр (л) — обозначается л. Литр равен 1 дециметру кубическому или 1000 кубическим сантиметрам.
• Кубический метр (м3) — обозначается м3. Это объем, занимаемый кубом со стороной длиной 1 метр.

Для перевода единиц объема друг в друга используются математические формулы и соотношения.

Овладение понятием единиц измерения объема позволяет ученикам более глубоко понять пространственные отношения и решать задачи, связанные с определением объема различных геометрических тел и контейнеров.

Объем прямоугольного параллелепипеда

Для вычисления объема прямоугольного параллелепипеда необходимо знать его три размера: длину, ширину и высоту.

Обозначим эти размеры соответственно через a, b и c.

Тогда формула для вычисления объема V прямоугольного параллелепипеда имеет вид:

V = a * b * c

Таким образом, чтобы найти объем прямоугольного параллелепипеда, необходимо перемножить его три размера.

Например, если длина параллелепипеда равна 5 единиц, ширина — 3 единицы, а высота — 2 единицы, то объем будет:

V = 5 * 3 * 2 = 30 единиц кубических.

Таким образом, ответом на задачу будет 30 единиц кубических.

Объем цилиндра

Объем цилиндра — это количество пространства, занимаемого цилиндром. Обозначается буквой V.

Объем цилиндра можно найти с помощью следующей формулы:

V = Sосн * h,

где Sосн — площадь основания цилиндра, а h — высота цилиндра.

Чтобы найти площадь основания цилиндра, нужно знать его форму. Основание цилиндра может быть кругом или многоугольником. Если основание цилиндра — круг, то площадь основания можно найти по формуле:

Sосн = π * r2,

где π (пи) — это математическая константа, приближенное значение которой равно 3,14, а r — радиус основания цилиндра.

Если же основание цилиндра — многоугольник, то площадь основания можно найти с помощью специальных формул для различных видов многоугольников.

Теперь, когда мы знаем площадь основания цилиндра и его высоту, можем легко найти объем цилиндра, подставив значения в формулу.

Объем пирамиды

Формула для вычисления объема пирамиды:

Объем = (Площадь основы * Высота) / 3

Для вычисления объема пирамиды необходимо знать единицы измерения площади и высоты в одних и тех же единицах измерения.

Пример задачи:

Найдите объем пирамиды, у которой площадь основы равна 36 квадратных сантиметров, а высота равна 10 сантиметров.

Решение:

Объем = (36 * 10) / 3 = 120 кубических сантиметров

Таким образом, объем пирамиды равен 120 кубическим сантиметрам.

Задачи на вычисление объема

Для расчета объема различных геометрических фигур используются разные формулы. Вот несколько задач, в которых нужно вычислить объем:

1. Задача 1: Найдите объем прямоугольного параллелепипеда со сторонами 4 см, 6 см и 8 см.
2. Задача 2: Какой будет объем цилиндра, если радиус его основания равен 5 см, а высота – 10 см?
3. Задача 3: Вычислите объем шара с радиусом 3 см.
4. Задача 4: Найдите объем пирамиды с основанием в виде квадрата со стороной 5 см и высотой 6 см.
5. Задача 5: Какой будет объем конуса, если его высота равна 12 см, а радиус основания – 4 см?

В этих задачах необходимо применять соответствующие формулы для вычисления объема различных фигур. Примите во внимание единицы измерения, указанные в задаче, и не забывайте подставить значения в формулу, чтобы получить ответ.

Решая задачи на вычисление объема, вы не только развиваете навыки применения математических формул, но и учитесь пространственно мыслить, что является важным навыком для решения различных задач в жизни.

Практическое применение понятия объема

Понятие объема широко применяется в реальной жизни и играет важную роль в различных областях. Рассмотрим несколько примеров практического применения данного понятия.

В строительстве объем используется для расчета необходимого количества строительных материалов. Например, зная объем помещения, можно определить количество кирпичей или плитки, необходимых для отделки.

В медицине объем используется для расчетов дозировки лекарств. Например, врач может рассчитать объем необходимого лекарственного препарата исходя из массы пациента и рекомендуемой дозы на единицу массы.

В транспорте объем применяется для расчета грузоподъемности транспортных средств. Например, зная объем грузовика, можно определить максимально возможный объем перевозимого груза.

Понимание и умение применять понятие объема помогают решать реальные задачи и делают математику полезной и применимой в повседневной жизни.

Вопрос-ответ:

Что такое объем?

Объем — это величина, которая показывает, сколько места занимает тело. Он измеряется в кубических единицах (кубический сантиметр, кубический метр и т.д.). Для каждого тела, в зависимости от его формы, существует своя формула для вычисления объема.

Как вычислить объем параллелепипеда?

Объем параллелепипеда можно вычислить по формуле: V = a * b * h, где a, b и h — это длина, ширина и высота параллелепипеда соответственно. Нужно просто перемножить эти три значения и получить объем в кубических единицах.

Какие основные понятия связаны с объемом?

Основными понятиями, связанными с объемом, являются единицы измерения объема (например, кубический сантиметр, кубический метр и т.д.), формулы для вычисления объема различных тел (например, параллелепипеда, шара, цилиндра и т.д.), а также свойства объема (например, свойство аддитивности, которое позволяет складывать объемы нескольких тел).

Какие задачи могут быть связаны с объемом в 5 классе?

В 5 классе ученики могут решать задачи, связанные с вычислением объема простых тел, таких как параллелепипеды, шары, цилиндры и т.д. Они могут, например, вычислять объем аквариума, коробки, шарика и т.д. Также ученикам могут задавать задачи на нахождение одного измерения (например, высоты или ширины) тела, если известны другие измерения и его объем.