Что такое площадь третий класс математика

Узнайте, что такое площадь в математике для третьего класса. Узнайте, как измерять площадь и решать простые задачи на нахождение площади различных фигур. Познакомьтесь с основными понятиями и правилами для работы с площадью.

Площадь — это одно из фундаментальных понятий математики, которое изучают уже в третьем классе. Площадь помогает нам определить, сколько места занимает поверхность какого-либо объекта. Она может быть измерена в квадратных единицах длины, таких как квадратные метры или квадратные сантиметры. Понимание площади является важным для решения различных задач и применения математических знаний в повседневной жизни.

Уроки математики для третьего класса часто включают задания по расчету площади различных фигур — квадратов, прямоугольников, треугольников и т. д. Для этого используются простые формулы и методы измерения. Разобравшись с понятием площади, ученики могут оценивать размеры и степень заполненности различных объектов, а также сравнивать их между собой.

Знание площади и умение ее вычислять пригодятся детям не только в школе, но и в дальнейшей жизни. Оно поможет им в решении задач по планированию пространства, покупке материалов для строительства или ремонта, расчете площади комнат и мебели.

В данной статье мы рассмотрим основные понятия площади, способы ее измерения, а также приведем примеры задач, которые помогут третьеклассникам лучше понять и применять это понятие в своей жизни.

Определение понятия «площадь»

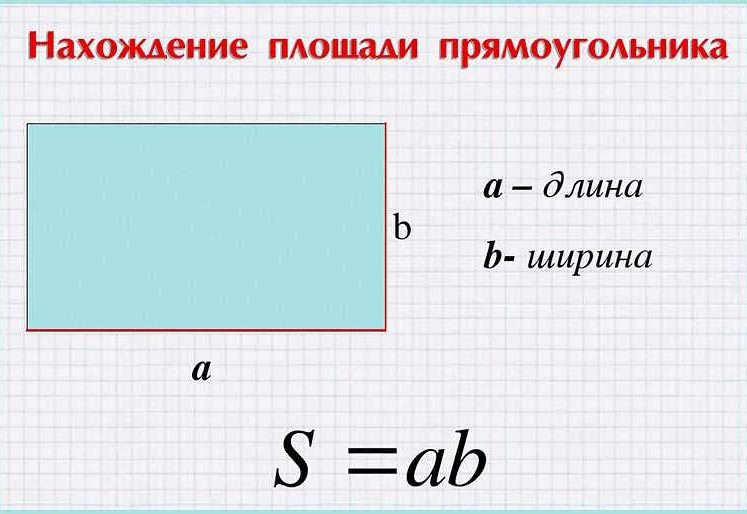
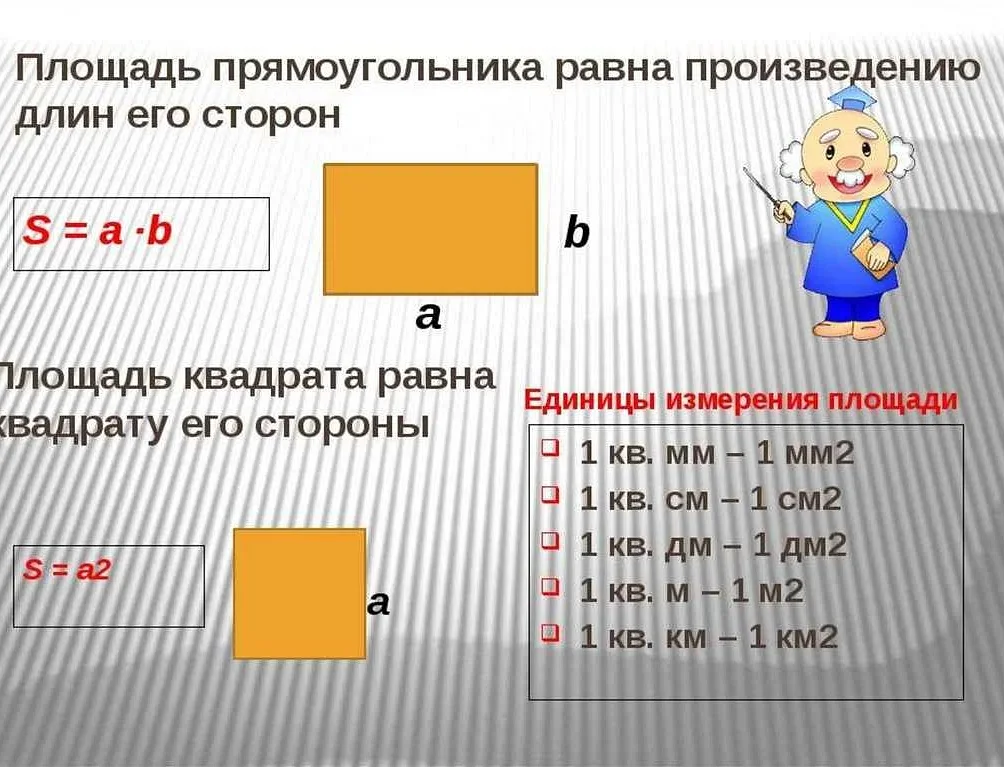
Для каждой фигуры существует своя формула, по которой можно вычислить ее площадь. Например, для прямоугольника площадь вычисляется по формуле: площадь = длина × ширина.

Для фигур с более сложной формой, таких как треугольник или круг, существуют свои формулы для вычисления площади. Например, для треугольника площадь вычисляется по формуле: площадь = (основание × высота) / 2. А для круга площадь вычисляется по формуле: площадь = π × радиус^2, где π — математическая константа, приближенное значение которой равно 3,14.

Зная формулу и значения соответствующих параметров, можно легко вычислить площадь фигуры. Вычисление площади позволяет узнать, сколько площади занимает определенная фигура на плоскости или в пространстве.

ФигураФормула для вычисления площади

Прямоугольник	площадь = длина × ширина
Треугольник	площадь = (основание × высота) / 2
Круг	площадь = π × радиус^2

Видео по теме:

Как измерить площадь?

Есть несколько способов измерить площадь различных фигур:

• Площадь прямоугольника можно вычислить, умножив длину одной из его сторон на длину другой стороны.
• Площадь квадрата можно найти, умножив длину его стороны на эту же длину.
• Площадь треугольника можно найти, умножив длину одной из его сторон на высоту, опущенную на эту сторону, а затем разделив полученный результат на 2.
• Площадь круга можно найти, умножив квадрат радиуса на число Пи (π).

Для измерения площади фигур с необычной формой, таких как фигуры с кривыми линиями, необходимо использовать специальные методы, такие как интегрирование или аппроксимация.

Измерение площади важно во многих областях, таких как строительство, геометрия, картография и другие. Знание, как измерять площадь, позволяет более точно определить размеры и форму различных объектов.

Формулы для расчета площади

Для квадрата площадь можно найти, умножив длину одной из его сторон на эту же длину: П = a * a, где «a» – длина стороны квадрата.

Для прямоугольника площадь также можно найти, умножив длину одной из его сторон на длину другой стороны: П = a * b, где «a» и «b» – длины сторон прямоугольника.

Для треугольника площадь можно найти, умножив длину одной из его сторон на высоту, опущенную на эту сторону: П = (a * h) / 2, где «a» – длина стороны треугольника, «h» – высота, опущенная на эту сторону.

Для круга площадь можно найти, умножив квадрат радиуса на число «π» (пи): П = π * r2, где «r» – радиус круга.

Зная формулы для расчета площади различных фигур, можно легко находить их площадь, используя известные значения сторон или радиуса.

ФигураФормула для расчета площади

Квадрат	П = a * a
Прямоугольник	П = a * b
Треугольник	П = (a * h) / 2
Круг	П = π * r2

Вопрос-ответ:

Что такое площадь?

Площадь — это мера площади или покрытия поверхности. В математике площадь измеряется в квадратных единицах, таких как квадратные сантиметры или квадратные метры. Например, если у нас есть прямоугольник со сторонами 5 сантиметров и 3 сантиметра, то его площадь равна 15 квадратным сантиметрам.

Как найти площадь прямоугольника?

Для нахождения площади прямоугольника нужно умножить длину одной стороны на длину другой стороны. Например, если длина одной стороны равна 6 сантиметров, а длина другой стороны равна 4 сантиметрам, то площадь прямоугольника будет равна 24 квадратным сантиметрам.

Как найти площадь круга?

Для нахождения площади круга нужно умножить квадрат радиуса круга на число Пи (примерно равное 3.14). Формула для вычисления площади круга: S = π * r^2, где S — площадь, π — число Пи, r — радиус круга. Например, если радиус круга равен 5 сантиметров, то площадь круга будет примерно равна 78.5 квадратным сантиметрам.

Что такое единица площади?

Единица площади — это стандартная единица измерения площади. В разных странах могут использоваться разные единицы площади. Например, в России и большинстве стран мира наиболее распространенные единицы площади — квадратные метры и квадратные сантиметры.

Можете привести еще примеры для вычисления площади?

Конечно! Допустим, у нас есть треугольник с высотой 8 сантиметров и основанием 6 сантиметров. Чтобы найти площадь треугольника, нужно умножить половину основания на высоту треугольника. В данном случае, площадь треугольника будет равна 24 квадратным сантиметрам. Еще один пример: у нас есть квадрат со стороной 10 сантиметров, чтобы найти площадь квадрата, нужно умножить длину стороны на саму себя. В данном случае, площадь квадрата будет равна 100 квадратным сантиметрам.

Что такое площадь?

Площадь — это мера площадной области, она показывает, сколько плоскости охватывает поверхность объекта или фигуры.

Можно ли измерить площадь любой фигуры?

Да, можно измерить площадь любой фигуры, если известны ее размеры или можно их определить. Для прямоугольников и квадратов площадь равна произведению длины на ширину, для треугольников — половина произведения длины основания на высоту, а для кругов — площадь равна произведению квадрата радиуса на число Пи.

Практические примеры из жизни

Понимание площади очень полезно в повседневной жизни. Например, когда мы покупаем ковер или линолеум для комнаты, нам нужно знать площадь этой комнаты, чтобы определить, сколько материала нам понадобится. Также, зная площадь квартиры или дома, мы можем рассчитать стоимость ремонта или покраски стен.

Еще один пример из жизни, где понимание площади пригодится, — это огород. Если у нас есть участок земли, на котором мы хотим выращивать овощи и фрукты, то нам нужно знать площадь этого участка. Это позволит нам определить, сколько растений мы можем посадить и где лучше разместить грядки.

Также, площадь может быть полезна в строительстве. Например, если мы планируем построить бассейн или террасу, нам нужно знать площадь этой конструкции, чтобы правильно подобрать материалы и распределить зоны отдыха.

В общем, понимание понятия площади помогает нам во многих сферах жизни. Оно позволяет нам рассчитывать материалы, планировать пространство и принимать рациональные решения. Поэтому изучение площади важно для нас всех.

Площадь различных фигур

Рассмотрим площади различных геометрических фигур:

1. Четырехугольники:

— Прямоугольник – площадь прямоугольника вычисляется по формуле: S = a * b, где a и b – длины сторон прямоугольника.

— Квадрат – площадь квадрата вычисляется по формуле: S = a * a, где a – длина стороны квадрата.

2. Треугольник:

— Прямоугольный треугольник – площадь прямоугольного треугольника вычисляется по формуле: S = (a * b)/2, где a и b – длины катетов треугольника.

— Обычный треугольник – площадь обычного треугольника вычисляется по формуле Герона: S = √p * (p — a) * (p — b) * (p — c), где a, b и c – длины сторон треугольника, а p – полупериметр треугольника.

3. Круг:

— Круг – площадь круга вычисляется по формуле: S = π * r * r, где π (пи) – математическая константа, равная примерно 3.14159, а r – радиус круга.

Зная формулы для вычисления площадей различных фигур, можно легко найти их площадь, используя известные значения длин сторон или радиусов.

Задачи на вычисление площади

Чтобы решить задачи на вычисление площади, необходимо знать формулы для различных фигур. Например, для прямоугольника площадь вычисляется по формуле: S = a * b, где a и b — длины сторон прямоугольника.

Для квадрата площадь вычисляется по формуле: S = a * a, где a — длина стороны квадрата.

Другие задачи могут требовать вычисления площади треугольника, круга или параллелограмма. Для каждой фигуры существуют соответствующие формулы для вычисления площади.

Задачи на вычисление площади часто встречаются в повседневной жизни. Например, при покупке ковра нужно знать его площадь, чтобы правильно подобрать размер. Также, площадь используется при замерах участков земли, раскладке плитки или паркета и во многих других ситуациях.

Вычисление площади — это важный навык, который помогает в решении различных задач и применении математики в повседневной жизни.

Интересные факты о площади

1. Самая большая площадь имеет поверхность Земли. Ее площадь составляет около 510 миллионов квадратных километров.
2. Самая маленькая площадь имеет точка. У точки площадь равна нулю, так как она не занимает никакой поверхности.
3. Квадрат со стороной длиной 1 метр имеет площадь 1 квадратный метр. Это единица площади, которую мы используем в повседневной жизни.
4. Площадь прямоугольника можно найти, умножив длину его стороны на ширину.
5. Площадь треугольника можно найти, умножив половину основания на высоту.
6. Круг имеет особую форму и для его площади используется формула: площадь круга равна произведению числа Пи на квадрат радиуса круга.
7. Узнать площадь фигуры помогает измерение длин сторон или радиусов, а также применение соответствующих формул.

Знание о площади помогает нам понять, сколько пространства занимает объект, решать задачи по геометрии и использовать математические знания в повседневной жизни.