Что такое площадь в математике формула

Площадь в математике — это величина, обозначающая площадь поверхности или фигуры. Рассчитывается с помощью соответствующей формулы для каждого конкретного случая. В данной статье рассмотрены основные формулы для расчета площади различных геометрических фигур и поверхностей. Узнайте, как использовать эти формулы для нахождения площади треугольников, прямоугольников, кругов, параллелограммов и других геометрических фигур.

Площадь — одно из основных понятий в математике, которое широко применяется в геометрии и физике. Она позволяет измерить поверхность фигуры и вычислить количество пространства, которое она занимает. Понимание площади является важным для решения задач, связанных с планированием, строительством и другими областями науки.

Для вычисления площади различных фигур применяются разные формулы. Например, для прямоугольника площадь равна произведению длины одной стороны на длину другой стороны. Для круга площадь вычисляется с помощью формулы, основанной на радиусе и числе π. Для треугольника существует формула Герона, которая зависит от длин всех его сторон.

Важно отметить, что для вычисления площади фигуры необходимо знать ее размеры. Это могут быть длины сторон, радиус, высота и другие характеристики, которые задаются в условии задачи.

Понимание основных принципов вычисления площади позволяет решать разнообразные задачи, связанные с нахождением площади фигур. Это могут быть задачи на построение, определение площади земельного участка, расчет площади пола и другие. Знание формул и способов вычисления площади позволяет не только получать правильные ответы, но и развивать логическое мышление и навыки решения задач в области математики.

Что такое площадь в математике?

Для вычисления площади различных фигур используются разные формулы. Например, для прямоугольника площадь вычисляется как произведение длины и ширины, для круга — как квадрат радиуса, умноженный на число Пи.

Определение площади имеет большое практическое значение. Например, зная площадь поля, можно определить, сколько растений можно вырастить на этой площади. Также площадь используется в архитектуре, геометрии, географии и других областях науки и техники.

ФигураФормула для вычисления площади

Прямоугольник	Площадь = длина × ширина
Круг	Площадь = Пи × радиус²
Треугольник	Площадь = (основание × высота) / 2

Определение понятия «площадь»

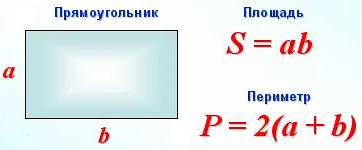
Для вычисления площади различных геометрических фигур существуют специальные формулы. Например, площадь прямоугольника вычисляется как произведение длины и ширины, а площадь круга — как квадрат радиуса, умноженный на число Пи.

Кроме того, площадь может быть вычислена с использованием интегралов в случае сложных фигур или поверхностей. Интегрирование позволяет разбить поверхность на бесконечно малые элементы и сложить их площади для получения общей площади.

Понимание площади в математике играет важную роль во многих областях, таких как геометрия, физика, строительство и другие. Вычисление площади позволяет определить, сколько пространства занимает определенная фигура или поверхность, и может быть полезным для решения различных практических задач.

Зачем нужно вычислять площадь?

Вычисление площади позволяет решать широкий спектр задач. Например, при планировании строительства дома необходимо знать площадь участка, чтобы определить, сколько материалов требуется для его ограждения или какую площадь займет сам дом. Площадь также важна при расчете стоимости отделки помещения или площади для засева на полях.

Вычисление площади позволяет нам также изучать свойства различных фигур и поверхностей. Например, площадь треугольника помогает нам определить его тип (равносторонний, равнобедренный или разносторонний) и связанные с ним свойства. Знание площади круга позволяет нам определить его радиус или диаметр.

Вычисление площади имеет также практическое применение в географии, архитектуре, строительстве, садоводстве и других областях. Понимание понятия площади и умение вычислять ее помогает нам более эффективно использовать ресурсы и решать различные задачи, связанные с пространственными объектами.

Таким образом, вычисление площади является важной и неотъемлемой частью математики и имеет широкое применение во многих областях нашей жизни.

Основные принципы вычисления площади

1. Для прямоугольника площадь вычисляется по формуле: площадь = длина × ширина. Данная формула применяется только для прямоугольной фигуры.

2. Для квадрата площадь также вычисляется по формуле: площадь = сторона × сторона. Квадрат является частным случаем прямоугольника, поэтому формула совпадает.

3. Для треугольника площадь можно вычислить по формуле: площадь = (основание × высота) / 2. Здесь основание — одна из сторон треугольника, а высота — расстояние от основания до противоположного угла.

4. Для круга площадь вычисляется по формуле: площадь = π × радиус², где π — приблизительно равно 3,14, а радиус — расстояние от центра круга до его границы.

5. Для фигуры со сложной формой, площадь может быть вычислена с использованием различных методов, таких как разбиение фигуры на простые геометрические фигуры или использование интеграла.

Вычисление площади является важным навыком, который применяется во многих областях науки и техники. Понимание основных принципов вычисления площади поможет в решении различных задач и позволит получить точные результаты.

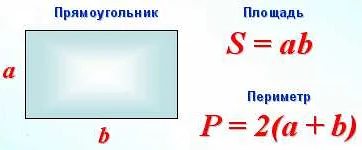
Формула для вычисления площади прямоугольника

ФормулаОбозначение

Площадь прямоугольника

S = a * b

Где:

• S — площадь прямоугольника
• a — длина одной стороны прямоугольника
• b — длина другой стороны прямоугольника

Для вычисления площади прямоугольника достаточно знать длины его сторон. Если длины сторон измеряются в одной и той же единице измерения, то и площадь будет измеряться в квадратных единицах этой же величины. Например, если сторона прямоугольника измеряется в метрах, то площадь будет измеряться в квадратных метрах.

Формула для вычисления площади треугольника

Формула для вычисления площади треугольника имеет вид:

S = (a * h) / 2

где:

S — площадь треугольника;

a — длина одной из сторон треугольника;

h — высота, опущенная на данную сторону треугольника.

Высота треугольника — это отрезок, проведенный из вершины треугольника к противолежащей стороне и перпендикулярный ей.

Используя данную формулу, можно вычислить площадь треугольника, зная длину одной из его сторон и высоту, опущенную на эту сторону. Вычисленная площадь будет выражена в квадратных единицах, например, в квадратных сантиметрах или квадратных метрах.

Важно помнить, что для правильного вычисления площади треугольника необходимо знать длину одной из его сторон и соответствующую высоту. Также следует учитывать, что данная формула применима только к треугольникам, у которых высота опущена на одну из сторон.

Формула для вычисления площади круга

Формула для вычисления площади круга выглядит следующим образом:

Площадь круга = π * R²

где:

• π (пи) — математическая константа, приближенно равная 3.14159;
• R — радиус круга.

Для применения формулы необходимо знать значение радиуса круга. Радиус — это расстояние от центра круга до его границы. Подставив значение радиуса в формулу, можно легко вычислить площадь круга.

Например, если радиус круга равен 5, то площадь круга будет:

Площадь круга = 3.14159 * 5² = 3.14159 * 25 = 78.53975.

Таким образом, площадь круга с радиусом 5 равна 78.53975 квадратных единиц.

Формула для вычисления площади круга является одной из основных формул в геометрии и находит широкое применение в различных областях, таких как инженерия, физика, архитектура и др.

Видео по теме:

Вопрос-ответ:

Зачем нужно вычислять площадь?

Вычисление площади позволяет определить площадь поверхности фигуры или площадь ограниченной фигурой области. Это важное понятие в математике, которое находит свое применение во многих областях, включая геометрию, физику и архитектуру. Знание площади позволяет решить множество задач, связанных с расчетами, планированием и построением.

Как вычислить площадь прямоугольника?

Формула для вычисления площади прямоугольника проста: площадь равна произведению длины на ширину. Если длина прямоугольника равна L, а ширина равна W, то площадь равна S = L * W.

Как вычислить площадь круга?

Для вычисления площади круга используется формула: S = π * r^2, где S — площадь, π — математическая константа, приближенно равная 3,14, а r — радиус круга. Простым способом вычислить площадь круга можно умножив квадрат радиуса на число π.

Как вычислить площадь треугольника?

Площадь треугольника можно вычислить по формуле Герона: S = √(p * (p — a) * (p — b) * (p — c)), где S — площадь треугольника, p — полупериметр, a, b, c — длины сторон треугольника. Другой способ вычисления площади треугольника — по формуле S = (a * h) / 2, где a — длина основания треугольника, h — высота, опущенная на основание.

Как вычислить площадь фигуры со сложной формой?

Площадь фигуры со сложной формой можно вычислить, разбив ее на простые геометрические фигуры, для которых известны формулы вычисления площади. Затем найденные площади суммируются. Например, если фигура можно разбить на два прямоугольника и треугольник, то площадь всей фигуры будет равна сумме площадей этих трех фигур.

Как вычислить площадь прямоугольника?

Площадь прямоугольника вычисляется по формуле: S = a * b, где a — длина стороны прямоугольника, b — ширина стороны прямоугольника.

Площадь и единицы измерения

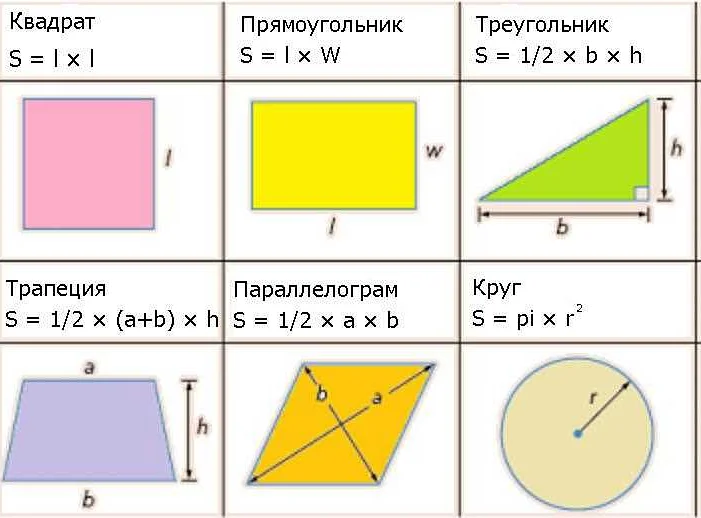
Площадь обычно вычисляется с использованием специальных формул, соответствующих каждому типу фигуры. Например, для прямоугольника площадь вычисляется как произведение длины на ширину: S = a * b, где S — площадь, a — длина, b — ширина.

Единицы измерения площади могут быть различными в зависимости от системы измерения, используемой в стране или области. Наиболее распространенными единицами измерения площади являются квадратные метры (м²) и квадратные сантиметры (см²).

Кроме того, существуют другие единицы измерения площади, такие как квадратные километры (км²), квадратные миллиметры (мм²), квадратные дециметры (дм²) и т.д. Используемая единица измерения зависит от масштаба объекта, который мы измеряем.

Для перевода площади из одной единицы измерения в другую используются специальные коэффициенты. Например, 1 квадратный метр равен 10000 квадратным сантиметрам, поэтому чтобы перевести площадь из метров в сантиметры, нужно умножить на 10000.

Знание различных единиц измерения площади важно при решении задач и проведении измерений в различных областях, таких как архитектура, строительство, география и др.

Примеры вычисления площади различных фигур

Рассмотрим примеры вычисления площади различных фигур:

1. Прямоугольник:

   Площадь прямоугольника можно вычислить, умножив длину одной из его сторон на длину другой стороны. Например, для прямоугольника со сторонами 4 и 6 единиц площадь будет равна 4 * 6 = 24 единицы.

2. Квадрат:

   Площадь квадрата можно вычислить, умножив длину одной из его сторон на саму себя. Например, для квадрата со стороной 5 единиц площадь будет равна 5 * 5 = 25 единиц.

3. Треугольник:

   Площадь треугольника можно найти, умножив половину произведения длин основания и высоты треугольника. Например, для треугольника с основанием 8 единиц и высотой 6 единиц площадь будет равна (8 * 6) / 2 = 24 единицы.

4. Круг:

   Площадь круга можно вычислить, умножив квадрат радиуса на число Пи (π). Например, для круга с радиусом 3 единицы площадь будет равна 3 * 3 * π = 9π единиц.