Что такое поле в математическом анализе

Поле в математическом анализе — это множество элементов, на котором определены операции сложения и умножения, удовлетворяющие определенным свойствам. Поля широко применяются в различных областях математики, физики и других наук. В данной статье мы рассмотрим основные понятия и свойства полей, а также их применение в различных математических и физических моделях.

Поле в математическом анализе — это алгебраическая структура, состоящая из непустого множества элементов, на котором определены две бинарные операции: сложение и умножение. Поля являются основой для изучения арифметических операций и свойств чисел.

Определение поля состоит из нескольких основных свойств. Во-первых, в поле должно быть определено сложение, которое обладает свойствами коммутативности, ассоциативности, существования нулевого элемента и существования противоположного элемента. Во-вторых, должно быть определено умножение, которое также обладает свойствами коммутативности, ассоциативности, существования единичного элемента и существования обратного элемента для каждого ненулевого элемента. Наконец, сложение и умножение должны обладать свойством дистрибутивности.

Поля широко используются в математике и ее приложениях. Они являются основой для изучения алгебры, анализа, топологии и других областей математики. Поля также используются в физике, экономике, компьютерных науках и других научных и инженерных дисциплинах.

Примеры полей включают в себя множество рациональных чисел, действительных чисел и комплексных чисел. Эти поля обладают всеми необходимыми свойствами и являются основными объектами изучения в анализе и алгебре.

Поле в математическом анализе: основные понятия и свойства

1. Замкнутость относительно сложения и умножения: Для любых элементов a и b из поля их сумма a + b и произведение a * b также принадлежат к данному полю.

2. Ассоциативность сложения и умножения: Для любых элементов a, b и c из поля выполняются следующие равенства: (a + b) + c = a + (b + c) и (a * b) * c = a * (b * c).

3. Коммутативность сложения и умножения: Для любых элементов a и b из поля выполняются следующие равенства: a + b = b + a и a * b = b * a.

4. Существование нейтральных элементов: В поле существуют нейтральные элементы относительно сложения (ноль) и умножения (единица), такие что для любого элемента a из поля выполняются равенства: a + 0 = a и a * 1 = a.

5. Существование обратных элементов: Для каждого ненулевого элемента a из поля существует обратный элемент относительно сложения (обратный по отношению к a) и обратный элемент относительно умножения (обратный по отношению к a), такие что выполняются равенства: a + (-a) = 0 и a * (1/a) = 1.

6. Дистрибутивность: Для любых элементов a, b и c из поля выполняются следующие равенства: a * (b + c) = a * b + a * c и (a + b) * c = a * c + b * c.

Таким образом, поле в математическом анализе обладает рядом важных свойств, которые позволяют проводить операции сложения и умножения с элементами данного поля.

Видео по теме:

Определение поля в математическом анализе

Поле обозначается символом F и состоит из элементов, называемых полями, которые могут быть числами, векторами или другими математическими объектами. Операция сложения в поле обозначается символом +, а операция умножения — символом *.

Основные свойства поля:

1. Закон сложения: для любых двух элементов a и b в поле F, их сумма a + b также является элементом поля F.
2. Закон умножения: для любых двух элементов a и b в поле F, их произведение a * b также является элементом поля F.
3. Ассоциативность сложения и умножения: для любых трех элементов a, b и c в поле F, сумма (a + b) + c равна a + (b + c), и произведение (a * b) * c равно a * (b * c).
4. Коммутативность сложения и умножения: для любых двух элементов a и b в поле F, сумма a + b равна b + a, и произведение a * b равно b * a.
5. Существование нейтрального элемента: в поле F существуют элементы 0 и 1, называемые нейтральными элементами относительно сложения и умножения соответственно, такие что для любого элемента a в поле F, a + 0 = a и a * 1 = a.
6. Существование обратного элемента: для любого элемента a в поле F, существуют элементы -a и 1/a, такие что a + (-a) = 0 и a * (1/a) = 1.
7. Дистрибутивность: для любых трех элементов a, b и c в поле F, выполняется закон дистрибутивности a * (b + c) = (a * b) + (a * c).

Примерами полей являются множество действительных чисел R, множество комплексных чисел C и множество рациональных чисел Q.

ОперацияОбозначениеПример

Сложение	+	3 + 4 = 7
Умножение	*	3 * 4 = 12

Алгебраическая структура поля

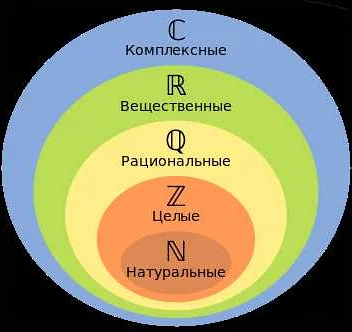
Основные свойства поля:

1. Закон сложения: для любых элементов a и b из поля их сумма a + b также является элементом поля.
2. Закон умножения: для любых элементов a и b из поля их произведение a * b также является элементом поля.
3. Коммутативность сложения: для любых элементов a и b из поля выполняется равенство a + b = b + a.
4. Коммутативность умножения: для любых элементов a и b из поля выполняется равенство a * b = b * a.
5. Ассоциативность сложения: для любых элементов a, b и c из поля выполняется равенство (a + b) + c = a + (b + c).
6. Ассоциативность умножения: для любых элементов a, b и c из поля выполняется равенство (a * b) * c = a * (b * c).
7. Существование нейтрального элемента по сложению: существует элемент 0, такой что для любого элемента a из поля выполняется равенство a + 0 = a.
8. Существование нейтрального элемента по умножению: существует элемент 1, такой что для любого элемента a из поля выполняется равенство a * 1 = a.
9. Существование обратного элемента по сложению: для любого элемента a из поля существует элемент -a, такой что a + (-a) = 0.
10. Существование обратного элемента по умножению: для любого элемента a из поля, кроме нуля, существует элемент a-1, такой что a * a-1 = 1.
11. Дистрибутивность умножения относительно сложения: для любых элементов a, b и c из поля выполняется равенство a * (b + c) = (a * b) + (a * c).

Поля являются основным объектом изучения в алгебре и широко применяются в различных областях математики и ее приложениях.

Вопрос-ответ:

Что такое поле в математическом анализе?

Поле в математическом анализе — это структура, состоящая из множества элементов, на котором определены операции сложения и умножения, удовлетворяющие некоторым аксиомам. Основные свойства поля включают ассоциативность, коммутативность, существование нейтральных элементов относительно сложения и умножения, существование обратного элемента относительно сложения и умножения, а также дистрибутивность умножения относительно сложения.

Какие операции определены на поле?

На поле определены операции сложения и умножения. Сложение — это операция, которая принимает два элемента из поля и возвращает их сумму. Умножение — это операция, которая принимает два элемента из поля и возвращает их произведение. Обе операции должны удовлетворять определенным аксиомам, чтобы поле могло считаться корректной математической структурой.

Какие свойства должно удовлетворять поле?

Поле должно удовлетворять нескольким основным свойствам. Во-первых, операция сложения должна быть ассоциативной и коммутативной. Это означает, что для любых трех элементов a, b и c из поля, справедливы равенства: (a + b) + c = a + (b + c) и a + b = b + a. Во-вторых, операция умножения должна быть ассоциативной и коммутативной. То есть, для любых трех элементов a, b и c из поля, должны выполняться равенства: (a * b) * c = a * (b * c) и a * b = b * a. Кроме того, поле должно содержать нейтральные элементы относительно сложения и умножения, а также обратные элементы относительно сложения и умножения. Наконец, умножение должно быть дистрибутивным относительно сложения.

Какие примеры полей существуют?

Примеры полей в математическом анализе включают множество рациональных чисел (Q), множество действительных чисел (R), множество комплексных чисел (C), а также множество остатков по модулю простого числа. Все эти множества образуют поля, так как удовлетворяют всем аксиомам, определяющим поле.

Основные операции в поле

Сложение — это операция, которая соответствует обычному сложению чисел. В поле сумма двух элементов также является элементом этого поля. Сложение обладает свойствами коммутативности, ассоциативности и существования нейтрального элемента.

Умножение — это операция, которая соответствует обычному умножению чисел. В поле произведение двух элементов также является элементом этого поля. Умножение обладает свойствами коммутативности, ассоциативности и существования нейтрального элемента.

В поле также выполняются свойства дистрибутивности сложения относительно умножения и ассоциативности умножения.

Обратные элементы — это элементы поля, которые при сложении с другими элементами дают нейтральный элемент ноль. Обратные элементы также могут существовать для операции умножения.

Нейтральный элемент — это элемент поля, который при сложении с другими элементами не изменяет их значения. В поле ноль является нейтральным элементом относительно сложения, а единица — относительно умножения.

Операции в поле позволяют выполнять арифметические операции над элементами поля, такие как сложение, умножение, вычитание и деление. Эти операции позволяют решать различные математические задачи и применять поле в различных областях науки и техники.

Свойства полей

1. Законы ассоциативности и коммутативности: в поле выполняются законы ассоциативности и коммутативности сложения и умножения. Это означает, что порядок выполнения операций не влияет на результат и что элементы можно менять местами без изменения результата.

2. Существование нейтральных элементов: в поле существуют нейтральные элементы относительно сложения и умножения. Нейтральный элемент сложения обозначается как 0 и удовлетворяет условию a + 0 = a для любого элемента a. Нейтральный элемент умножения обозначается как 1 и удовлетворяет условию a * 1 = a для любого элемента a.

3. Существование обратных элементов: в поле каждый ненулевой элемент имеет обратный элемент относительно умножения. Обратный элемент для элемента a обозначается как a-1 и удовлетворяет условию a * a-1 = 1.

4. Дистрибутивность: в поле выполняется закон дистрибутивности, который гласит, что для любых элементов a, b и c верно равенство a * (b + c) = a * b + a * c.

Эти свойства являются основными для полей и они позволяют проводить различные операции и доказывать теоремы в математическом анализе.

Поля в математической физике

В математической физике поле представляет собой основной объект изучения. Оно описывает распределение физической величины в пространстве и времени. Поле может быть скоростным, электрическим, магнитным, температурным и т.д.

Математически поле в математической физике представляется в виде функции, которая зависит от координат и времени. Эта функция называется полем, а значения этой функции в каждой точке — компонентами поля.

Для описания полей в математической физике используются уравнения поля, которые выражают зависимость компонент поля от координат и времени. Решение этих уравнений позволяет определить распределение поля в пространстве и времени.

Поля в математической физике имеют ряд основных свойств, таких как суперпозиция, линейность, сохранение энергии и импульса. Суперпозиция означает, что если в пространстве есть несколько полей, то общее поле будет равно сумме всех этих полей. Линейность означает, что уравнения поля являются линейными относительно компонент поля и их производных. Сохранение энергии и импульса означает, что поле сохраняет общую энергию и импульс в системе.

Поля в математической физике играют важную роль при решении физических задач. Они позволяют описать и предсказать различные физические явления, такие как движение тел, электромагнитные волны, теплопроводность и многие другие.

Расширение поля

В математическом анализе поле может быть расширено, то есть добавлены новые элементы, так называемые расширения поля. Расширение поля позволяет решать уравнения, которые в исходном поле не имеют решений.

Одним из примеров расширения поля является добавление к полю рациональных чисел поля иррациональных чисел, например, к полю рациональных чисел можно добавить число π. Таким образом, получается новое поле, в котором можно выполнять арифметические операции и решать уравнения, включающие иррациональные числа.

Расширение поля может быть конечным или бесконечным. Конечное расширение поля добавляет только конечное число новых элементов, в то время как бесконечное расширение поля добавляет бесконечное число новых элементов. Например, добавление к полю рациональных чисел всех алгебраических чисел (корней алгебраических уравнений) является бесконечным расширением поля.

Расширение поля имеет множество интересных свойств и приложений в математике и других науках. Оно позволяет решать более широкий класс уравнений, а также исследовать более сложные математические объекты. Расширение поля является одной из основных тем в алгебре и математическом анализе.

Поле и его связь с другими математическими конструкциями

Поле имеет тесную связь с другими математическими конструкциями, такими как группа и кольцо. Группа является более общим понятием, чем поле, и определяется только одной операцией, обладающей свойствами ассоциативности, коммутативности и существования обратного элемента. Кольцо, в свою очередь, является несколько более сложной структурой, так как на нем определены две операции, но они не всегда обладают свойством коммутативности.

Поле можно рассматривать как особый вид кольца, в котором все ненулевые элементы обратимы относительно умножения. Поэтому поле является обобщением понятия поля вещественных чисел, в котором любое ненулевое число имеет обратное число относительно умножения.

Связь полей с другими математическими конструкциями позволяет использовать понятие поля в различных областях математики, таких как линейная алгебра, алгебраическая геометрия, математическая физика и др. В этих областях поля используются для решения различных задач, включая системы линейных уравнений, анализ графов, построение кривых и поверхностей, моделирование физических явлений и т.д.

Примеры полей в математическом анализе

1. Поле действительных чисел (обозначается обычно символом $\mathbb{R}$) – это наиболее известное и широко используемое поле. В нем определены основные арифметические операции: сложение, вычитание, умножение и деление. Также имеются дополнительные свойства, например, свойство плотности числовой прямой.
2. Поле комплексных чисел (обозначается символом $\mathbb{C}$) – это расширение поля действительных чисел. В поле комплексных чисел определены арифметические операции, включая сложение, вычитание, умножение и деление. Особенностью комплексных чисел является наличие мнимой единицы $i$, которая удовлетворяет условию $i^2 = -1$. Поле комплексных чисел широко применяется в математике и физике.
3. Поле рациональных чисел (обозначается символом $\mathbb{Q}$) – это поле, состоящее из всех чисел, которые можно представить в виде дроби $\frac{a}{b}$, где $a$ и $b$ – целые числа, а $b$ не равно нулю. Поле рациональных чисел является подполем поля действительных чисел.
4. Поле остатков по модулю $n$ (обозначается символом $\mathbb{Z}_n$) – это поле, состоящее из классов эквивалентности целых чисел по модулю $n$, где $n$ – натуральное число. В поле остатков определены операции сложения и умножения, а также дополнительные свойства, связанные с арифметикой по модулю.

Это лишь некоторые примеры полей, используемых в математическом анализе. Каждое из этих полей имеет свои особенности и применения в различных областях математики и науки.