Что такое признак разбиения математика 1 класс петерсон

Признак разбиения в математике 1 класса Петерсона — это метод, который позволяет разделить множество на подмножества с определенными характеристиками. Узнайте, как применять этот признак в учебном процессе и как он помогает детям развивать логическое мышление и аналитические навыки.

Признак разбиения математика 1 класс Петерсон — это концепция, разработанная математическим педагогом Петерсоном, которая помогает детям лучше понимать и обрабатывать информацию о числах и их свойствах. Этот признак основывается на идее разбиения чисел на составляющие части, что позволяет ученикам легче решать математические задачи и улучшать свои навыки в этой области.

Основные понятия, связанные с признаком разбиения, включают цифры, числа, единицы, десятки и сотни. Цифры — это символы, которые используются для представления чисел. Числа — это комбинации цифр, которые имеют свои уникальные свойства и значения. Единицы представляют одиночные цифры, десятки — числа, оканчивающиеся на ноль, а сотни — числа, оканчивающиеся на два нуля.

Например, число 123 может быть разбито на единицы, десятки и сотни следующим образом: 1 единица, 2 десятка и 3 сотни. Это позволяет ученикам лучше понимать структуру чисел и их отношение друг к другу.

Признак разбиения математика 1 класса Петерсон используется в обучении математике, чтобы помочь детям развивать навыки анализа числовых данных и решать математические задачи более эффективно. Этот подход помогает ученикам увидеть взаимосвязь между числами и их составными частями, что способствует развитию их математического мышления и логического рассуждения.

Основные понятия и определения признака разбиения

Определение признака разбиения заключается в следующем: признак разбиения задает разбиение множества объектов на непересекающиеся подмножества, где каждое подмножество называется классом признака.

Классификация объектов с помощью признака разбиения осуществляется на основе свойств или характеристик, которые присущи каждому объекту. Например, можно использовать признак разбиения «цвет» для классификации фруктов на «красные», «желтые» и «зеленые».

Признак разбиения может быть задан в виде таблицы, где каждая строка представляет собой объект, а каждый столбец — характеристику признака. Значения в таблице указывают, присутствует или отсутствует данная характеристика у объекта.

Примеры признаков разбиения в математике включают такие понятия, как «четные» и «нечетные» числа, «простые» и «составные» числа, «треугольники» и «четырехугольники» и т.д.

Что такое признак разбиения в математике?

Для определения признака разбиения числа на два других числа, необходимо рассмотреть возможные комбинации сумм двух чисел. Если признак разбиения выполняется для данного числа, то оно называется разбиваемым числом, иначе — неразбиваемым числом.

Приведем примеры, чтобы лучше понять, что такое признак разбиения. Пусть у нас есть число 10. Чтобы определить, можно ли разложить число 10 на сумму двух других чисел, мы перебираем все возможные комбинации:

1 + 2 = 3	1 + 3 = 4	1 + 4 = 5	1 + 5 = 6	1 + 6 = 7	1 + 7 = 8	1 + 8 = 9	1 + 9 = 10
2 + 2 = 4	2 + 3 = 5	2 + 4 = 6	2 + 5 = 7	2 + 6 = 8	2 + 7 = 9	2 + 8 = 10
3 + 3 = 6	3 + 4 = 7	3 + 5 = 8	3 + 6 = 9	3 + 7 = 10
4 + 4 = 8	4 + 5 = 9	4 + 6 = 10
5 + 5 = 10

Из таблицы видно, что число 10 можно разложить на сумму двух других чисел: 1 и 9, 2 и 8, 3 и 7, 4 и 6, 5 и 5. Следовательно, число 10 является разбиваемым числом.

Признак разбиения имеет важное значение в алгебре, числовой теории и других областях математики, где требуется изучение структуры чисел и их свойств.

Определение признака разбиения

Признак разбиения может быть представлен в виде таблицы, где каждая строка представляет отдельный объект, а каждый столбец соответствует определенному признаку или характеристике. В каждой ячейке таблицы указывается соответствующее значение признака для данного объекта.

Примером признака разбиения может служить классификация фруктов по их цвету. В этом случае признаком будет цвет фрукта, а объектами — сами фрукты. Таблица признака разбиения может выглядеть следующим образом:

ФруктЦвет

Яблоко	Красный
Груша	Зеленый
Апельсин	Оранжевый
Банан	Желтый

По данной таблице можно разделить фрукты на группы в зависимости от их цвета. Например, все фрукты красного цвета будут отнесены к одной группе, фрукты зеленого цвета — к другой группе и т.д.

Примеры использования признака разбиения в математике 1 класса

Признак разбиения в математике 1 класса используется для разделения предметов на группы по их общим свойствам. Это помогает детям узнавать и классифицировать объекты вокруг себя.

Ниже приведены примеры использования признака разбиения в математике 1 класса:

Признак разбиенияПримеры

Форма	круг, квадрат, треугольник
Цвет	красный, синий, желтый
Размер	большой, маленький, средний
Материал	дерево, металл, пластик

Дети могут использовать признак разбиения, чтобы классифицировать игрушки, фрукты, животных и другие объекты. Например, они могут разделить игрушки на мягкие и твердые, фрукты на круглые и не круглые, а животных на домашних и диких.

Этот признак также может быть использован для сортировки и группировки объектов в математических играх и заданиях. Например, детям могут предложить разделить картинки на две группы: с животными и без животных, или с круглыми и некруглыми предметами.

Использование признака разбиения в математике 1 класса помогает детям развивать логическое мышление, учиться классифицировать объекты и узнавать их общие свойства.

Пример 1: Разбиение числа на слагаемые

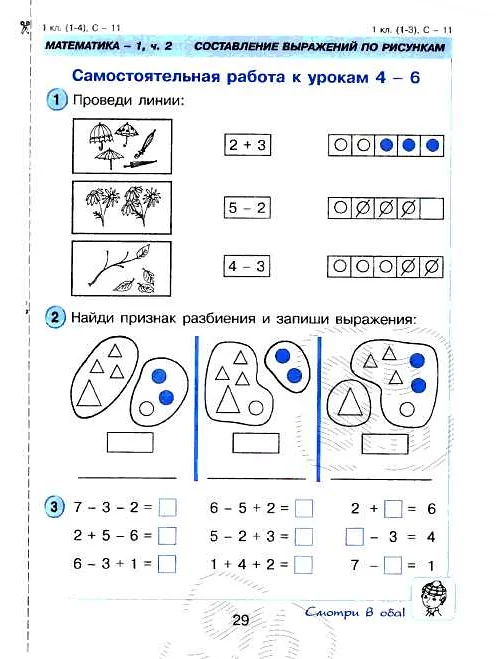
Рассмотрим пример разбиения числа 5 на слагаемые:

• 5 = 1 + 1 + 1 + 1 + 1
• 5 = 2 + 1 + 1 + 1
• 5 = 3 + 1 + 1
• 5 = 2 + 2 + 1
• 5 = 4 + 1
• 5 = 3 + 2
• 5 = 5

В каждом из этих разбиений числа 5 на слагаемые, мы получаем сумму, равную 5. При этом, каждое слагаемое может быть использовано только один раз в каждом разбиении.

Таким образом, разбиение числа на слагаемые представляет собой один из способов представления числа в виде суммы других чисел, и является важным признаком разбиения в математике.

Пример 2: Разбиение множества на подмножества

Рассмотрим множество A = {1, 2, 3, 4, 5, 6}.

Построим разбиение данного множества на подмножества по следующему правилу: каждый элемент множества должен принадлежать ровно одному подмножеству.

Разбиваем множество A на два подмножества:

A1 = {1, 3, 5} и A2 = {2, 4, 6}.

Таким образом, множество A разбито на два подмножества A1 и A2.

Это пример разбиения множества на подмножества, где каждый элемент принадлежит только одному подмножеству. Такие разбиения могут быть полезны при решении задач комбинаторики или при анализе данных.

Пример 3: Разбиение фигуры на части

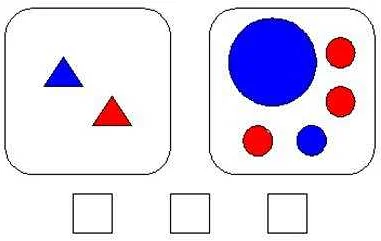
Рассмотрим пример разбиения фигуры на части. Представим, что у нас есть прямоугольная фигура, состоящая из 4 квадратов одинакового размера.

Мы можем разбить эту фигуру на две части, объединив квадраты в различные комбинации. Например, мы можем объединить квадраты красного и зеленого цветов в одну часть, а квадраты синего и желтого цветов в другую часть.

Таким образом, мы разбили исходную фигуру на две части.

Применение признака разбиения в жизни

Применение признака разбиения в жизни может быть очень полезным. Вот несколько примеров:

• При планировании своего дня можно использовать признак разбиения для определения времени на различные задачи. Например, разбить день на блоки времени для работы, отдыха, тренировок и т.д.
• При организации мероприятия можно использовать признак разбиения для разделения участников на группы или команды. Это поможет упростить процесс взаимодействия и сотрудничества.
• При изучении нового предмета или темы можно использовать признак разбиения для разделения информации на более мелкие части. Это поможет лучше понять и запомнить материал.
• При планировании бюджета можно использовать признак разбиения для разделения расходов по категориям. Это позволит более точно контролировать свои финансы.
• При решении сложной задачи можно использовать признак разбиения для разделения ее на более простые подзадачи. Это поможет упростить процесс решения и достичь лучших результатов.

Применение признака разбиения в жизни может помочь организовать время, ресурсы и информацию, делая процессы более эффективными и удобными.

Видео по теме:

Вопрос-ответ:

Что такое признак разбиения в математике?

Признак разбиения в математике это способ разделения множества на непересекающиеся подмножества.

Какие основные понятия связаны с признаком разбиения в математике?

Основные понятия, связанные с признаком разбиения в математике, это множество, подмножество и непересекающиеся множества.

Можете привести пример признака разбиения в математике?

Конечное множество {1, 2, 3, 4, 5} можно разбить на подмножества {1, 2}, {3, 4}, {5}, которые не пересекаются друг с другом.

Какие свойства имеет признак разбиения в математике?

Свойства признака разбиения в математике включают: каждый элемент множества должен принадлежать хотя бы одному подмножеству, каждые два подмножества должны либо не пересекаться, либо быть равными, и объединение всех подмножеств должно быть равно исходному множеству.

Какие применения имеет признак разбиения в математике?

Признак разбиения в математике имеет много применений, например, в теории множеств, комбинаторике, алгебре и других областях математики. Он помогает организовывать и классифицировать элементы множества и решать различные задачи на основе его свойств.

Какие основные понятия связаны с признаком разбиения в математике для 1 класса по учебнику Петерсона?

Основными понятиями, связанными с признаком разбиения, являются разбиение числа на слагаемые, количество слагаемых в разбиении и комбинация слагаемых в разбиении.

Применение признака разбиения в повседневной жизни

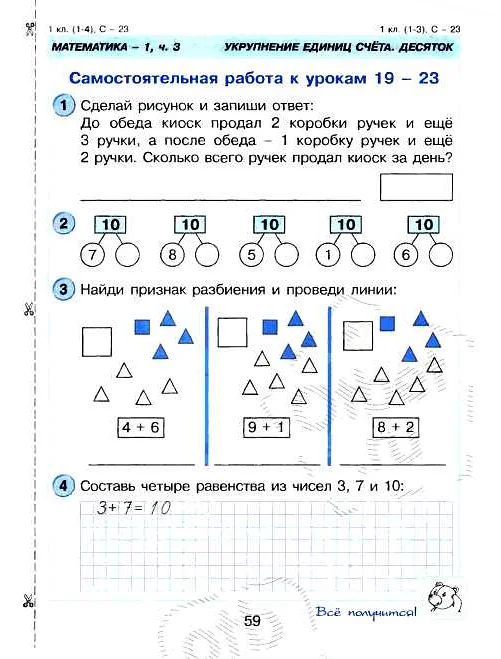
Одним из примеров использования признака разбиения в повседневной жизни является сортировка и классификация предметов в домашней библиотеке. При обустройстве своей коллекции книг можно использовать признаки разбиения, такие как жанр, автор, год выпуска и т.д. Это позволит легко находить нужные книги и создавать удобные разделы для их хранения.

Другим примером применения признака разбиения может быть организация продуктов в супермаркете. Продукты могут быть распределены по отделам или категориям, таким как молочные продукты, мясо и рыба, овощи и фрукты и т.д. Это помогает покупателям быстро находить нужные продукты и упрощает процесс покупок.

Также признак разбиения может быть использован для классификации одежды в гардеробе. По типу и сезону можно разделить одежду на категории: верхняя одежда, платья, брюки, футболки и т.д. Это позволяет быстро находить нужную одежду и создавать гармоничные образы.

Таким образом, признак разбиения является полезным инструментом в повседневной жизни, позволяющим классифицировать и организовывать объекты и явления в соответствии с их общими характеристиками.

Применение признака разбиения в науке

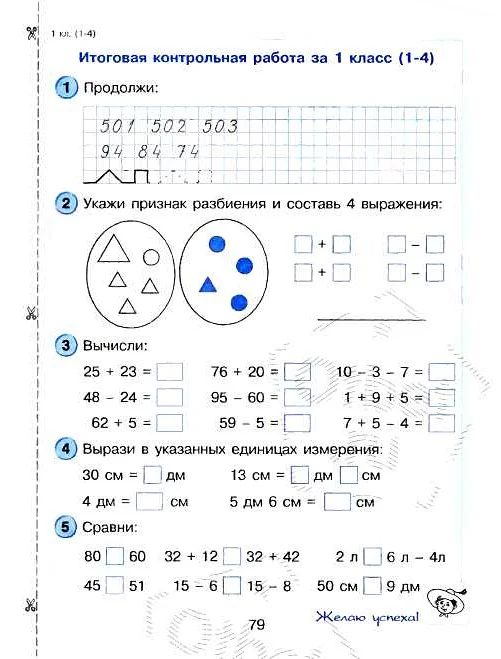
В науке признак разбиения используется для классификации и систематизации различных объектов и явлений. Например, в биологии этот признак используется для классификации живых организмов по таким признакам, как вид, род, семейство и так далее. Это позволяет биологам более точно изучать и описывать разнообразие живых существ.

В физике признак разбиения применяется для классификации элементарных частиц по их свойствам, например, массе, заряду и спину. Это помогает физикам понять особенности и взаимодействия различных частиц и строение физических систем.

В химии признак разбиения используется для классификации химических элементов по их химическим свойствам и строению. Это позволяет химикам систематизировать знания о химических элементах и использовать их в различных химических реакциях и процессах.

Применение признака разбиения в науке позволяет создавать более точные и удобные системы классификации объектов и явлений, что в свою очередь способствует более глубокому исследованию и пониманию различных научных дисциплин.