Что такое проценты в математике
Содержимое
- 1 Что такое проценты в математике
- 1.1 Проценты: определение и основные понятия
- 1.2 Видео по теме:
- 1.3 Как рассчитывать проценты: базовые формулы и правила
- 1.4 Примеры использования процентов в повседневной жизни
- 1.5 Вопрос-ответ:
- 1.5.0.1 Что такое проценты?
- 1.5.0.2 Как вычислить процент от числа?
- 1.5.0.3 Как найти число, если известен процент и его значение?
- 1.5.0.4 Как найти процент изменения?
- 1.5.0.5 Как выразить число в процентах?
- 1.5.0.6 Какое понятие лежит в основе процентов в математике?
- 1.5.0.7 Как вычислить процент от числа?
- 1.6 Проценты в финансовой сфере: ссуды, депозиты, инвестиции
- 1.7 Проценты в бизнесе: расчеты прибыли и убытков
- 1.8 Практические примеры решения задач с процентами
- 1.9 Значение процентов в статистике и исследованиях
- 1.10 Влияние процентов на экономику и общество
Проценты в математике – это способ представления долей и отношений в виде десятичных дробей или процентов. Узнайте, как рассчитывать проценты, как применять их для решения задач и как они связаны с долей и десятичными дробями.
Проценты – это одно из основных понятий в математике и финансовой сфере. Они позволяют измерять долю или часть от общей величины и широко применяются в различных сферах жизни. Понимание процентов необходимо для решения финансовых задач, планирования бюджета, расчета скидок и налогов, а также для анализа данных и статистики.
Проценты выражаются в виде десятичных дробей или десятичных дробей, умноженных на 100. Например, 0,25 (или 25/100) представляет собой 25 процентов. Проценты могут быть положительными и отрицательными, в зависимости от того, увеличивается или уменьшается исходная величина.
Примеры использования процентов:
— Расчет скидки на товар: если товар стоит 1000 рублей, а скидка составляет 10%, то сумма скидки будет равна 100 рублей.
— Расчет налога: если ставка налога составляет 15%, а доход равен 5000 рублей, то сумма налога будет равна 750 рублей.
— Анализ данных: если из 100 человек 25 процентов поддерживают определенную идею, то это означает, что 25 человек поддерживают данную идею.
Для расчета процентов существуют специальные формулы. Формула расчета процента от числа имеет вид: процент = число * процент / 100. Например, чтобы найти 10% от числа 200, необходимо умножить 200 на 10 и разделить на 100, получив результат равный 20. Формула расчета числа по проценту имеет вид: число = процент * 100 / процент. Например, чтобы найти число, соответствующее 25 процентам от числа 400, необходимо умножить 400 на 25 и разделить на 100, получив результат равный 100.
Проценты: определение и основные понятия
Основными понятиями в процентах являются процентное значение, процент и база.
Процентное значение — это число, которое указывает на долю или часть от 100. Например, если процентное значение равно 50, это означает, что это число составляет половину от целого числа 100.
Процент — это процентное значение, выраженное с использованием знака процента (%). Например, 25% означает 25 процентов или 25/100.
База — это целое число, относительно которого вычисляется процент. Например, если база равна 200, а процентное значение равно 50%, это означает, что 50% от 200 составляет 100.
Для вычисления процентов используется формула:
Процент = (Процентное значение / 100) * База
Например, чтобы вычислить 30% от числа 150, мы используем формулу:
Процент = (30 / 100) * 150 = 0.3 * 150 = 45
Таким образом, 30% от числа 150 равно 45.
Видео по теме:
Как рассчитывать проценты: базовые формулы и правила
Основные формулы и правила для расчета процентов:
- Процент от числа. Для расчета процента от числа умножьте число на процент и разделите на 100. Формула: Процент = (Число * Процент) / 100.
- Число, увеличенное на процент. Для расчета числа, увеличенного на процент, сложите число и процент от числа. Формула: Число + (Число * Процент) / 100.
- Число, уменьшенное на процент. Для расчета числа, уменьшенного на процент, вычтите процент от числа из самого числа. Формула: Число — (Число * Процент) / 100.
- Изменение числа в процентах. Для расчета изменения числа в процентах найдите разницу между двумя числами, разделите ее на исходное число и умножьте на 100. Формула: (Новое число — Исходное число) / Исходное число * 100.
Эти формулы являются базовыми и позволяют рассчитать различные виды процентов. Они могут быть использованы, например, для расчета скидок, налогов, процентных ставок, роста и падения показателей и т. д.
Помните, что правильное применение формул требует ясного определения величин и правильного учета знаков, чтобы получить точный результат. Также важно уметь интерпретировать полученный результат и применять его на практике.
Примеры использования процентов в повседневной жизни

1. Финансы: Проценты играют ключевую роль в финансовой сфере. Например, проценты используются для расчета процентных ставок по кредитам, депозитам и ипотекам. Также проценты помогают определить доходность инвестиций и сбережений.
2. Торговля: В розничной торговле проценты используются для расчета скидок и наценок. Например, магазины могут предложить скидку 20% на определенный товар или установить наценку 30% на стоимость товара.
3. Увеличение/уменьшение величин: Проценты также могут использоваться для увеличения или уменьшения величин. Например, если цена товара увеличилась на 10%, то новая цена будет равна старой цене плюс 10% от старой цены.
4. Скидки и распродажи: Проценты широко используются при организации скидок и распродаж. Например, магазин может предложить скидку 50% на весь ассортимент в определенный день или период.
5. Финансовые планирование: Проценты также играют важную роль в финансовом планировании. Например, при планировании пенсии, необходимо учитывать процентные ставки для определения необходимого накопления.
Таким образом, проценты являются неотъемлемой частью повседневной жизни и широко используются в различных областях, помогая нам сделать рациональные решения и оценить изменения величин.
Вопрос-ответ:
Что такое проценты?
Проценты — это способ представления доли или части от целого числа. Они используются для измерения и сравнения долей, а также для решения задач связанных с процентным выражением.
Как вычислить процент от числа?
Для вычисления процента от числа, нужно умножить это число на процент и разделить результат на 100. Например, чтобы найти 20% от числа 100, нужно выполнить следующую операцию: 100 * 20 / 100 = 20.
Как найти число, если известен процент и его значение?
Чтобы найти число, если известен процент и его значение, нужно разделить значение процента на процент и умножить результат на 100. Например, если известно, что 20% от числа равно 40, можно выполнить следующую операцию: 40 / 20 * 100 = 200.
Как найти процент изменения?
Чтобы найти процент изменения, нужно вычислить разницу между двумя значениями, разделить ее на исходное значение и умножить результат на 100. Например, если исходное значение равно 100, а новое значение равно 120, то процент изменения будет: (120 — 100) / 100 * 100 = 20%.
Как выразить число в процентах?
Чтобы выразить число в процентах, нужно умножить это число на 100 и указать знак процента. Например, если число равно 0.75, его можно выразить в процентах следующим образом: 0.75 * 100 = 75%.
Какое понятие лежит в основе процентов в математике?
Основой процентов в математике является понятие доли или части от целого числа. Проценты показывают, сколько частей от целого числа составляет данное число.
Как вычислить процент от числа?
Для вычисления процента от числа нужно умножить это число на десятичную дробь, соответствующую проценту. Например, чтобы найти 20% от числа 100, нужно умножить 100 на 0,2, что даст 20.
Проценты в финансовой сфере: ссуды, депозиты, инвестиции

Ссуды – это денежные средства, предоставляемые одним лицом другому на условиях возврата суммы займа и уплаты процентов за пользование этими средствами. Проценты по ссуде рассчитываются как процент от суммы займа и могут быть фиксированными или изменяемыми в зависимости от условий договора. Они служат компенсацией за риск, связанный с предоставлением займа.
Депозиты – это средства, которые физическое или юридическое лицо вносит на счет в банк на определенный срок с целью получения процентов от этой суммы. Процентная ставка по депозиту может быть фиксированной или изменяемой и определяется банком. Банк использует депозиты для кредитования и получает прибыль от разницы между процентной ставкой по депозиту и ставкой по кредитам.
Инвестиции – это вложение денежных средств в ценные бумаги, недвижимость, бизнес и другие активы с целью получения дохода. При инвестировании часто используется понятие процентной ставки, которая представляет собой ожидаемую доходность от инвестиций. Она может быть различной в зависимости от типа инвестиций и риска, связанного с ними.
В финансовой сфере проценты играют важную роль и позволяют определить доходность или расходность различных финансовых операций. Правильное использование и понимание процентов помогает принимать рациональные финансовые решения и управлять своими финансами.
Проценты в бизнесе: расчеты прибыли и убытков

Один из наиболее распространенных способов использования процентов в бизнесе — расчет процентной ставки по кредиту или вкладу. При взятии кредита предприниматель должен будет выплачивать проценты на сумму кредита, в то время как вкладчик получает проценты на свой вклад. Эти расчеты помогают определить затраты на заемные средства или доход от инвестирования.
Кроме того, проценты используются для расчета прибыли и убытков. Прибыль — это разница между доходами и расходами предприятия за определенный период времени. Расчет прибыли включает в себя учет процентов по заемным средствам, налогов и других расходов, которые влияют на финансовое состояние бизнеса. Убыток, в свою очередь, может быть вызван недостаточной прибылью или избыточными расходами.
В бизнесе проценты также используются для оценки эффективности инвестиций и финансовой устойчивости предприятия. Например, рентабельность инвестиций (ROI) — это показатель, который позволяет определить, сколько прибыли было получено от инвестирования в определенный проект или актив. Он рассчитывается путем деления прибыли на сумму инвестиции и умножения на 100%. Чем выше ROI, тем более успешной является инвестиция.
Таким образом, проценты в бизнесе играют важную роль при расчете прибыли, убытков, эффективности инвестиций и других финансовых показателей. Правильное использование процентов позволяет предпринимателям принимать обоснованные финансовые решения и эффективно управлять своим бизнесом.
Практические примеры решения задач с процентами
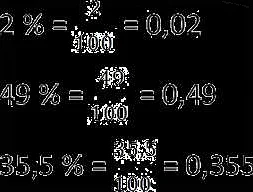
Проценты в математике используются для выражения отношения одного числа к другому в виде десятичной дроби. Рассмотрим несколько практических примеров решения задач с процентами.
Пример 1:
Сколько составляет 25% от числа 80?
ДействиеВычисление
| Найти 25% от 80 | 0.25 * 80 = 20 |
Ответ: 25% от числа 80 равно 20.
Пример 2:
На товар была установлена скидка в размере 15%. Сколько стоит товар после скидки, если его исходная цена составляет 2000 рублей?
ДействиеВычисление
| Вычислить сумму скидки | 0.15 * 2000 = 300 |
| Вычесть сумму скидки из исходной цены | 2000 — 300 = 1700 |
Ответ: после скидки товар будет стоить 1700 рублей.
Пример 3:
Депозит в банке предлагает годовой процентный доход в размере 4%. Какая сумма будет на счету через 5 лет, если внести на него 10000 рублей?
ДействиеВычисление
| Вычислить годовой доход | 0.04 * 10000 = 400 |
| Вычислить общую сумму через 5 лет | 10000 + (400 * 5) = 12000 |
Ответ: через 5 лет на счету будет 12000 рублей.
Это лишь несколько примеров использования процентов в решении задач. Зная основные формулы и правила, вы сможете успешно решать задачи с процентами в математике.
Значение процентов в статистике и исследованиях
Проценты играют важную роль в статистике и исследованиях, помогая представить информацию в более наглядной форме. Они используются для описания доли или частоты какого-либо явления в выборке или популяции. Значение процентов позволяет сравнивать различные группы, делать выводы о распределении данных и оценивать степень влияния различных факторов.
Примеры использования процентов в статистике:
- Выявление предпочтений: процентное соотношение может показать, какой процент опрошенных людей предпочитает один продукт или услугу по сравнению с другими.
- Анализ результатов опросов: проценты используются для анализа ответов на вопросы опросов, позволяя сделать выводы о распределении мнений и предпочтений.
- Исследование тенденций: проценты помогают отслеживать изменение доли какого-либо явления во времени, например, изменение популярности определенного продукта.
- Оценка влияния: проценты позволяют оценить влияние различных факторов на исследуемое явление, например, оценить влияние рекламной кампании на увеличение продаж.
Формула для расчета процента:
Процент = (Часть / Всего) * 100%
Где:
— Часть — количество или доля интересующего нас явления;
— Всего — общее количество или доля в выборке или популяции.
Знание процентов позволяет проводить более глубокий и точный анализ данных, делать выводы, основанные на фактических числах, и принимать обоснованные решения.
Влияние процентов на экономику и общество
Проценты влияют на рынок кредитования и финансовые операции. Они определяют стоимость заемных средств, а также доходность банковских и инвестиционных продуктов. Высокие процентные ставки могут ограничивать доступность кредитов и затруднять развитие малого и среднего бизнеса. Низкие проценты, напротив, способствуют повышению спроса на кредиты и инвестиции, стимулируя развитие экономики.
Проценты также влияют на инфляцию и уровень цен. Центральные банки часто используют процентные ставки как инструмент для контроля инфляции. Повышение процентных ставок может сдерживать рост цен, тогда как снижение процентов может способствовать стимулированию экономической активности и повышению уровня цен.
В обществе проценты имеют значительное влияние на финансовую грамотность и поведение людей. Понимание процентных ставок и их влияния помогает принимать осознанные финансовые решения, планировать бюджет, инвестировать и сберегать деньги. Однако, неправильное использование процентов, например, при неправильном управлении кредитами или накопления долгов, может привести к финансовым проблемам и долговой яме.
Таким образом, проценты играют важную роль в экономике и обществе, оказывая влияние на кредитование, инвестиции, инфляцию и финансовое поведение людей. Понимание понятия процентов и их важности в математике позволяет лучше ориентироваться в финансовом мире и принимать обоснованные решения в сфере личных финансов.

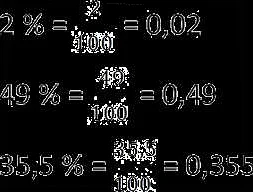



Очень интересная и познавательная статья! Я всегда задумывалась, что такое проценты и как они применяются в математике. Теперь я поняла, что процент — это доля от целого, которая выражается в сотых долях. Например, если товар стоит 1000 рублей, а скидка составляет 20%, то я сэкономлю 200 рублей. Формула для вычисления процента тоже кажется мне простой и понятной: процент = (число/целое число) * 100%. Благодаря этой статье, я теперь понимаю, как рассчитывать проценты и использовать их в повседневной жизни. Спасибо за такую полезную информацию! Жду новых статей на эту тему.