Определение произведения в математике для учащихся 5 класса

Произведение в математике в 5 классе – это результат умножения двух или более чисел. Определение произведения, примеры задач и правила умножения в 5 классе. Узнайте, как правильно решать задачи на произведение в 5 классе.

Произведение — это одна из основных операций в математике, которая позволяет узнать результат умножения двух или более чисел. В пятом классе ученики начинают изучать это понятие и осваивать его основные правила и свойства.

В математике произведение обозначается символом «×» или «*», и является одной из четырех основных арифметических операций, вместе с сложением, вычитанием и делением. Однако, в отличие от сложения и вычитания, произведение имеет свои особенности и правила, которые необходимо учесть при его выполнении.

Произведение двух чисел можно определить как сумму одного из этих чисел, взятого столько раз, сколько указано вторым числом. Например, произведение 3 и 4 равно 3 + 3 + 3 + 3, что равно 12.

Важно помнить, что операция умножения является коммутативной, то есть порядок чисел в произведении не важен.

На уроках математики в пятом классе ученики изучают различные способы вычисления произведения, например, с помощью таблицы умножения, долгим умножением или использованием свойств арифметических действий. Важно понимать, что правильное выполнение операции умножения требует внимательности и точности, поэтому необходимо не только знать правила, но и уметь применять их на практике.

Определение произведения

Произведение двух чисел a и b обозначается символом «×» или знаком умножения. Например, произведение чисел 3 и 4 можно записать как 3 × 4 = 12.

Произведение чисел можно вычислить путем повторения сложения одного числа несколько раз. Например, произведение чисел 3 и 4 можно вычислить как 3 + 3 + 3 + 3 = 12.

Произведение коммутативно, то есть порядок сомножителей не важен. Например, произведение чисел 3 и 4 равно произведению чисел 4 и 3: 3 × 4 = 4 × 3 = 12.

Произведение числа на 1 равно этому числу: a × 1 = a.

Произведение числа на 0 равно 0: a × 0 = 0.

Видео по теме:

Примеры произведений

Вот несколько примеров произведений:

Пример 1: Произведение чисел 3 и 4 равно 12: 3 * 4 = 12.

Пример 2: Произведение чисел 5, 2 и 6 равно 60: 5 * 2 * 6 = 60.

Пример 3: Произведение чисел 7 и 9 равно 63: 7 * 9 = 63.

Пример 4: Произведение чисел 10 и 0 равно 0: 10 * 0 = 0.

Таким образом, произведение чисел можно вычислять, перемножая их.

Правила умножения чисел

1. Умножение на 0 всегда даёт 0. Произведение любого числа на 0 равно 0.
2. Умножение на 1 не меняет число. Произведение любого числа на 1 равно этому числу.
3. Умножение на 10, 100, 1000 и т.д. равно умножению числа на соответствующее количество нулей и добавлению их в конец числа. Например, 5 * 10 = 50, 7 * 100 = 700.
4. Умножение числа на 10, 100, 1000 и т.д. сдвигает его разрядность на соответствующее количество разрядов влево. Например, умножение числа 123 на 10 даёт 1230.
5. Умножение двузначного числа на однозначное число производится путём умножения каждого разряда первого числа на второе число и сложения результатов. Например, 25 * 3 = 75.
6. Умножение многозначного числа на однозначное число производится путём умножения каждого разряда первого числа на второе число, начиная с младшего разряда, и записи результатов в столбик. Затем все результаты складываются. Например, 123 * 4 = 492.

Эти правила умножения помогают ученикам освоить умножение чисел разной разрядности и выполнять умножение без ошибок. С их помощью можно решать математические задачи и применять умножение в повседневной жизни.

Вопрос-ответ:

Что такое произведение в математике?

Произведение в математике — это операция, которая позволяет найти результат умножения двух или более чисел. В результате умножения получается новое число, которое называется произведением.

Как определить произведение в математике?

Произведение в математике определяется как результат умножения двух или более чисел. Для определения произведения необходимо умножить все числа, указанные в задаче или уравнении, и получить новое число — произведение.

Какие есть примеры произведений в математике?

Примерами произведений в математике могут быть, например, умножение чисел 5 и 7, что даст произведение 35; умножение чисел 3, 4 и 2, что даст произведение 24; умножение чисел 9 и 0, что даст произведение 0. Произведение может быть как положительным, так и отрицательным числом.

Какие свойства имеет произведение в математике?

Произведение в математике обладает несколькими свойствами. Например, произведение числа на 1 равно этому числу, т.е. a * 1 = a. Также произведение числа на 0 равно 0, т.е. a * 0 = 0. Кроме того, произведение чисел можно менять местами без изменения результата, т.е. a * b = b * a. Это лишь некоторые из свойств произведения в математике.

Какую роль играет произведение в математике?

Произведение играет важную роль в математике, так как часто используется для решения различных задач и уравнений. Оно позволяет умножать числа, находить площади прямоугольников и квадратов, находить объемы фигур, решать пропорции и многое другое. Произведение также имеет важное значение в алгебре и других разделах математики.

Что такое произведение в математике?

Произведение в математике — это результат умножения двух или более чисел. В умножении числа на число получается новое число, которое называется произведением. Например, произведение чисел 3 и 4 равно 12.

Как определить произведение чисел?

Произведение чисел можно определить путем умножения. Для умножения необходимо взять два или более числа, найти их произведение путем повторения сложения одного из этих чисел несколько раз. Например, произведение чисел 3 и 4 равно 12, так как 3+3+3=9, а 9+3=12.

Свойства произведения

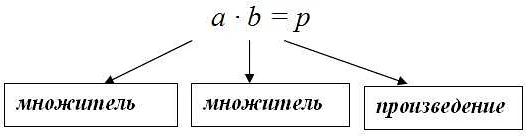
Произведение двух чисел можно записать в виде умножения:

Если числа a и b являются множителями, то их произведение обозначается как a × b.

Свойства произведения:

1. Произведение любого числа a на 1 равно самому числу: a × 1 = a.
2. Произведение двух чисел не зависит от порядка умножения: a × b = b × a.
3. Произведение трех и более чисел также не зависит от порядка умножения: a × b × c = c × b × a.
4. Произведение числа на ноль равно нулю: a × 0 = 0.
5. Произведение двух отрицательных чисел всегда положительно: (-a) × (-b) = a × b.
6. Произведение чисел a и b равно нулю, если хотя бы одно из них равно нулю: a × b = 0, если a = 0 или b = 0.

Примеры:

5 × 1 = 5

2 × 3 = 3 × 2 = 6

4 × 0 = 0

(-2) × (-3) = 2 × 3 = 6

7 × 0 = 0

Знание свойств произведения помогает в решении задач и упрощении выражений с умножением.

Произведение и операции

Произведение двух чисел a и b можно найти путем повторения сложения одного из этих чисел a раз. Например, произведение 3 и 4 равно 3 + 3 + 3 + 3 = 12.

Основные свойства произведения:

— Произведение двух чисел не зависит от порядка этих чисел. Например, 3 × 4 = 4 × 3 = 12.

— Произведение числа на единицу равно этому числу. Например, 5 × 1 = 5.

— Произведение числа на ноль равно нулю. Например, 2 × 0 = 0.

Произведение также может быть найдено путем использования таблицы умножения или использования калькулятора. Всегда важно проверять правильность произведения, особенно при работе с большими числами или при использовании десятичных дробей.

Произведение и действия

Произведение двух чисел обозначается символом «×» или «*», и записывается в виде a × b или a * b, где a и b — множители. Множитель a называется первым множителем, а множитель b — вторым множителем.

Произведение можно представить как сложение нескольких одинаковых чисел. Например, произведение 3 × 4 можно понять как сумму трех чисел 4: 4 + 4 + 4 = 12. Также можно представить произведение как повторение одного числа несколько раз. Например, 5 × 2 можно понять как повторение числа 5 два раза: 5 + 5 = 10.

Произведение чисел имеет несколько свойств:

• Коммутативность: порядок множителей не важен, a × b = b × a;
• Ассоциативность: результат умножения не зависит от расстановки скобок, (a × b) × c = a × (b × c);
• Существование нейтрального элемента: умножение числа на 1 не изменяет его значение, a × 1 = a;
• Свойство нуля: умножение числа на ноль всегда дает ноль, a × 0 = 0.

Произведение часто используется для решения задач, связанных с количеством объектов или суммой элементов. Оно также является одной из основных операций в алгебре и математическом анализе.

Значение произведения

Значение произведения зависит от значений множителей. Если оба множителя положительные, то и произведение будет положительным. Если один из множителей отрицательный, то и произведение будет отрицательным. Если один из множителей равен нулю, то и произведение будет равно нулю.

Произведение может быть использовано для нахождения площади прямоугольника. Если длина прямоугольника равна a, а ширина равна b, то площадь прямоугольника равна a × b.

Произведение также может быть использовано для нахождения общей стоимости нескольких одинаковых предметов. Если стоимость одного предмета равна a, а количество предметов равно b, то общая стоимость будет равна a × b.

Применение произведения в реальной жизни

Произведение можно применить в различных ситуациях. Например, если у вас есть коробка с яблоками, а вы хотите узнать, сколько яблок в коробке всего, вы можете использовать произведение. Допустим, в коробке 5 рядов яблок, а в каждом ряду по 3 яблока. Тогда произведение 5 * 3 покажет вам, что в коробке всего 15 яблок.

Другой пример — расчет площади прямоугольника. Если у вас есть прямоугольник, у которого одна сторона равна 4 см, а другая сторона равна 6 см, то произведение этих двух чисел, то есть 4 * 6, даст вам площадь прямоугольника, которая будет равна 24 квадратным сантиметрам.

Произведение также может быть использовано для расчета общей стоимости покупки. Если у вас есть несколько товаров, каждый из которых стоит определенную сумму денег, и вы хотите узнать, сколько вам придется заплатить за все товары вместе, вы можете умножить цену каждого товара на его количество и сложить полученные значения. Например, если у вас есть 3 книги, каждая из которых стоит 200 рублей, то произведение 3 * 200 покажет вам, что вам нужно заплатить 600 рублей за все книги.

Таким образом, произведение является важной математической операцией, которая имеет практическое применение в различных ситуациях реальной жизни. Оно позволяет узнать количество объектов, площадь или общую стоимость, используя заданные числа и операцию умножения.