Что такое составная задача в математике

Составная задача в математике — это задача, которая состоит из нескольких частей или шагов, которые нужно выполнить, чтобы получить окончательный результат. В этой статье вы узнаете, как решать составные задачи и какие методы использовать при их решении.

Составная задача — это задача, которая состоит из нескольких связанных между собой частей и требует решения каждой части отдельно, а затем объединения полученных результатов для получения окончательного решения. В математике составные задачи позволяют применить знания и навыки, полученные в разных областях математики, для решения сложных проблем.

Составные задачи могут включать в себя различные математические операции, такие как сложение, вычитание, умножение и деление, а также более сложные концепции, такие как пропорции, проценты и вероятность. Они могут иметь разные формы, такие как текстовые задачи, графики, таблицы или графы. Однако важно понимать, что составная задача требует не только математического анализа, но и логического мышления и умения видеть связи между различными элементами задачи.

Примером составной задачи может быть задача о покупке продуктов в магазине. В этой задаче нужно посчитать общую стоимость покупки, учитывая цены на продукты и количество каждого продукта, а затем решить, сколько денег у покупателя осталось после покупки, если он заплатил определенную сумму. Для решения этой задачи необходимо применять навыки сложения, умножения и вычитания, а также использовать понятия процентов и дробей.

Составные задачи являются важным элементом математического образования, так как они помогают студентам развивать аналитическое мышление, умение анализировать сложные ситуации и применять математические знания на практике. Они также помогают студентам видеть связи между математикой и реальными жизненными ситуациями, что помогает им лучше понимать и оценивать информацию вокруг себя.

Определение составной задачи в математике

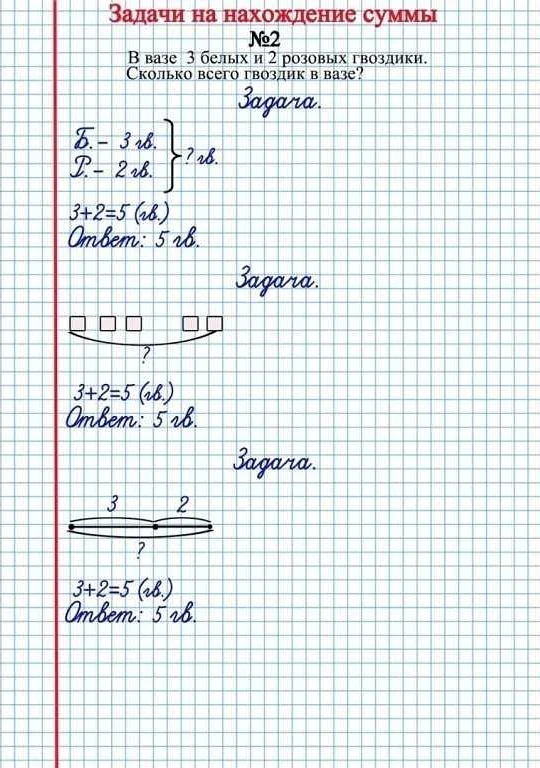
Особенностью составной задачи является то, что она объединяет различные аспекты математики, такие как геометрия, алгебра, арифметика и другие. В процессе решения составной задачи необходимо анализировать информацию, проводить логические рассуждения, применять соответствующие формулы и методы решения задач.

Чтобы успешно решить составную задачу, необходимо разбить ее на отдельные подзадачи и последовательно решать их. Каждая подзадача может иметь свои собственные условия и требования, и решение одной подзадачи может служить основой для решения следующей. В конечном итоге, решив все подзадачи, можно получить окончательный ответ на основную составную задачу.

Примером составной задачи может служить задача о построении треугольника, в которой необходимо найти длины сторон и вычислить площадь. Для решения этой задачи требуется знание формул для вычисления длин сторон треугольника и его площади, а также умение применять эти формулы в конкретной ситуации.

Примеры составных задач в математике

Пример 1:

На ферме есть 20 коров и 10 кур. Каждая корова дает 3 литра молока в день, а каждая курица — 1 яйцо. Через сколько дней общее количество молока и яиц превысит 100?

Решение:

Сначала нужно посчитать, сколько молока дает каждая корова в день: 20 коров × 3 литра/корова = 60 литров молока в день.

Затем нужно посчитать, сколько яиц дает каждая курица в день: 10 кур × 1 яйцо/курица = 10 яиц в день.

Теперь нужно найти, через сколько дней общее количество молока и яиц превысит 100:

60 литров молока/день + 10 яиц/день = 70 единиц продукции/день.

100 единиц продукции ÷ 70 единиц/день = 1.43 дня.

Таким образом, через 2 дня общее количество молока и яиц превысит 100.

Пример 2:

Анна и Билл катаются на велосипедах. Анна двигается со скоростью 15 км/ч, а Билл — со скоростью 20 км/ч. Если они встречаются каждый день на одной точке пути, через сколько времени они снова встретятся?

Решение:

Для того чтобы найти время, через которое они снова встретятся, нужно найти наименьшее общее кратное (НОК) между скоростями движения Анны и Билла.

НОК(15, 20) = 60.

Таким образом, Анна и Билл снова встретятся через 60 минут, то есть через 1 час.

Пример 3:

На столе лежит коробка с треугольным пазлом. Каждая сторона пазла состоит из разноцветных треугольников. Сколько треугольников составляют пазл, если общее количество его сторон равно 12?

Решение:

Так как каждая сторона пазла состоит из треугольников, общее количество треугольников в пазле будет равно половине от общего количества его сторон.

Количество треугольников = 12 сторон ÷ 2 = 6 треугольников.

Таким образом, в пазле составляют 6 треугольников.

Составная задача: особенности и основные элементы

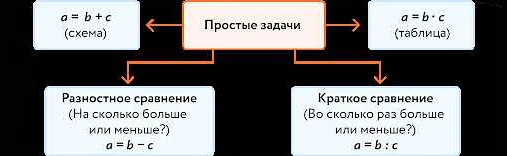
Составная задача в математике представляет собой задачу, которая состоит из нескольких связанных между собой подзадач. Она требует применения нескольких математических понятий, операций и алгоритмов для ее решения.

Основные особенности составной задачи:

• Сложность. Составные задачи обычно являются более сложными и требуют глубокого понимания математических концепций.
• Связность. Подзадачи составной задачи взаимосвязаны и зависят друг от друга. Решение одной подзадачи может влиять на решение других.
• Многоэтапность. Решение составной задачи требует последовательного выполнения нескольких этапов и шагов.

Основные элементы составной задачи:

• Исходные данные. В составной задаче приводятся начальные условия, на основе которых нужно найти решение.
• Подзадачи. Составная задача разбивается на несколько подзадач, каждая из которых имеет свою цель и требует определенных вычислений.
• Связи между подзадачами. Подзадачи составной задачи взаимосвязаны и зависят друг от друга. Решение каждой подзадачи может влиять на решение других.
• Результат. Решение составной задачи представляет собой конечный результат, который может быть числовым, графическим или текстовым.

Примером составной задачи может быть задача о планировании поездки. Для ее решения необходимо определить бюджет, выбрать маршрут, рассчитать расходы на транспорт и проживание, а также учесть другие факторы, такие как время и погодные условия.

Как решать составные задачи в математике

Решение составных задач в математике может быть сложным, так как требует анализа и разбиения задачи на более простые подзадачи. Однако, с правильным подходом и использованием определенных стратегий, можно успешно решить даже самые сложные составные задачи.

1. Внимательное чтение и понимание условий задачи: Перед тем, как приступить к решению, необходимо внимательно прочитать условия задачи и уяснить, что от вас требуется. Обратите внимание на ключевые слова и числовые данные.

2. Разбиение задачи на подзадачи: Когда вы полностью понимаете условия задачи, можно приступать к разбиению ее на более простые подзадачи. Разбивайте задачу на шаги и обозначайте каждый шаг цифрой или буквой. Это поможет вам легче ориентироваться в решении.

3. Использование известных математических концепций и формул: Вам могут понадобиться знания и понимание определенных математических концепций или формул, чтобы решить составную задачу. Примените эти знания и используйте соответствующие формулы для решения каждой подзадачи.

4. Постепенное решение каждой подзадачи: Начните с решения самой простой подзадачи, а затем постепенно переходите к более сложным. Решайте каждую подзадачу последовательно, используя логику и математические навыки.

5. Проверка и анализ полученного решения: После того, как вы решили все подзадачи, необходимо проверить полученное решение. Проанализируйте результаты и убедитесь, что они соответствуют условиям задачи и логике.

Важно помнить, что решение составной задачи в математике требует терпения, внимания к деталям и умения разбивать сложные задачи на более простые подзадачи. Постепенно практикуйтесь в решении таких задач, и вы заметите, что с каждым разом это будет становиться все проще и легче.

Практическое применение составных задач в математике

Составные задачи в математике имеют важное практическое применение в различных областях жизни. Они помогают развивать навыки анализа, логического мышления и применения математических концепций для решения сложных проблем.

Одной из областей, где составные задачи широко используются, является финансовая сфера. Например, при планировании инвестиций или расчете процентных ставок, математические модели могут быть использованы для определения наиболее выгодных вариантов или предсказания будущих результатов.

Еще одним практическим применением составных задач является оптимизация процессов. В производственном секторе, например, математические модели могут помочь определить оптимальное распределение ресурсов или наилучший способ выполнения задачи, что позволяет сэкономить время и деньги.

В медицинской области составные задачи могут быть использованы для оценки эффективности лечения или прогнозирования развития болезней. Анализ математических данных может помочь врачам принимать взвешенные решения и оптимизировать пациентское лечение.

Кроме того, составные задачи имеют широкое применение в технических и инженерных расчетах. Они могут быть использованы для моделирования и расчета различных физических явлений, определения надежности систем или прогнозирования поведения материалов.

Таким образом, составные задачи представляют собой мощный инструмент для решения сложных задач в различных областях. Они помогают применять математические концепции на практике и находить оптимальные решения для реальных проблем.

Составная задача в школьной программе

Такие задачи помогают развивать не только навыки решения простых математических задач, но и способность структурировать информацию и анализировать сложные ситуации. Решение составной задачи требует умения понимать условие задачи, а также определять последовательность действий для достижения желаемого результата.

Примером составной задачи может быть задача, связанная с покупкой и продажей товаров. В условии задачи могут быть даны данные о ценах на различные товары и количество товаров, которое нужно купить или продать. Ученик должен рассчитать общую стоимость покупки или продажи, учитывая различные факторы, такие как скидки или налоги.

ТоварЦена за единицуКоличество

Молоко	50 рублей	2 литра
Хлеб	30 рублей	3 буханки
Яйца	5 рублей	10 штук

Например, для решения такой задачи ученику нужно умножить цену за единицу на количество товара и затем сложить полученные значения. Он также может применить скидку или налог, если это указано в условии задачи. В результате решения всех подзадач ученик получит общую стоимость покупки или продажи товаров.

Составные задачи развивают умение анализировать информацию и применять математические навыки для решения сложных ситуаций. Они помогают школьникам развивать логическое мышление и применять полученные знания на практике.

Видео по теме:

Вопрос-ответ:

Что такое составная задача в математике?

Составная задача в математике — это задача, которая состоит из нескольких подзадач или этапов, требующих решения последовательно. Она может включать в себя различные математические операции и концепции, которые нужно применять для получения окончательного результата.

Какие примеры можно привести составных задач в математике?

Один из примеров составной задачи в математике — это задача про покупку продуктов в магазине. В этой задаче необходимо сначала посчитать общую стоимость продуктов, затем вычесть из нее скидку, если она предоставляется, и, наконец, рассчитать итоговую сумму, которую нужно заплатить. Другим примером может быть задача про постройку фигуры из геометрических форм, где нужно сначала вычислить площадь каждой формы, а затем сложить их все вместе.

Чем отличается составная задача от простой задачи в математике?

Составная задача отличается от простой задачи тем, что она состоит из нескольких этапов или подзадач, в то время как простая задача решается одним шагом или операцией. В составной задаче требуется выполнить несколько математических операций последовательно для получения окончательного результата, в то время как в простой задаче достаточно выполнить одно действие или операцию для получения ответа.

Как решать составные задачи в математике?

Для решения составных задач в математике следует следовать нескольким шагам. Сначала необходимо внимательно прочитать условие задачи и понять, какие подзадачи или этапы нужно выполнить. Затем следует определить, какие математические операции применить к каждому этапу и последовательно выполнять их. Наконец, нужно объединить результаты каждого этапа, чтобы получить окончательный ответ. Важно следить за правильной последовательностью выполнения операций и внимательно проверять свои вычисления.

Значение составных задач в развитии учащихся

Составные задачи в математике играют важную роль в развитии учащихся. Они помогают ученикам развивать логическое мышление, аналитические навыки и способность применять полученные знания на практике.

Решение составных задач требует от учащихся умения анализировать и разбивать сложные проблемы на более простые подзадачи. Это способствует развитию их критического мышления и способности видеть связи между различными аспектами задачи.

Кроме того, составным задачам часто необходимо применять математические знания из разных областей, что помогает учащимся понимать, как математика связана с реальным миром и как ее можно применять в повседневной жизни. Это позволяет ученикам увидеть практическую ценность математических знаний и мотивирует их к изучению этого предмета.

Решение составных задач также развивает у учащихся терпение, настойчивость и умение работать в команде. Часто составные задачи требуют совместной работы и обмена идеями между учащимися, что помогает развивать навыки сотрудничества и коммуникации.

Таким образом, составные задачи являются не только важным инструментом для развития математических навыков, но и помогают учащимся развивать целый ряд навыков и качеств, которые будут полезны им в жизни.

Советы по решению составных задач в математике

Решение составных задач в математике может быть сложным, но с правильным подходом и стратегией можно успешно справиться с ними. Вот несколько советов, которые помогут вам разобраться с составными задачами:

1. Читайте задачу внимательно и несколько раз. Убедитесь, что вы понимаете, что требуется найти или решить. Обратите внимание на все данные, условия и ограничения.

2. Разбейте задачу на более простые подзадачи. Иногда составные задачи могут быть разделены на несколько более простых задач, которые легче решаются по отдельности. Разделите задачу на несколько этапов и решайте их по очереди.

3. Используйте схемы и диаграммы. Визуализация может помочь вам понять и организовать информацию. Рисуйте диаграммы, стрелки, таблицы и другие графические элементы, чтобы визуально представить свои мысли.

4. Применяйте известные методы и формулы. Если в задаче присутствуют знакомые формулы или методы, используйте их для нахождения ответа. Не забывайте о простых математических операциях, таких как сложение, вычитание, умножение и деление.

5. Проверяйте свои ответы. После того, как вы решите составную задачу, перечитайте условие и убедитесь, что ваш ответ соответствует требуемому результату. Если есть возможность, проверьте свой ответ другим способом или используйте контрольные значения, если они имеются.

С учетом этих советов вы сможете эффективно решать составные задачи в математике и повысить свои навыки анализа и решения сложных проблем.