Что такое таблица пифагора в математике

Таблица Пифагора — это специальная таблица, которая позволяет быстро и удобно умножать числа от 1 до 10. Она основана на свойствах треугольника Пифагора и может быть полезной для учащихся и студентов при выполнении математических задач и расчетов.

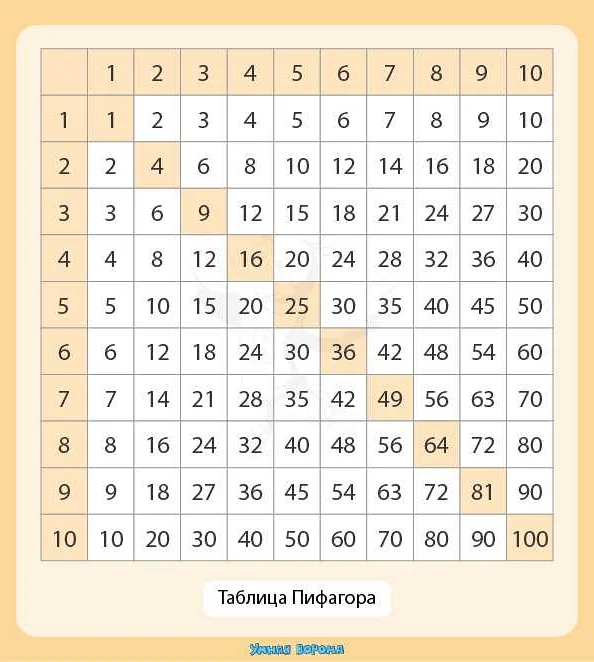
Таблица Пифагора — это наглядный способ представления умножения чисел от 1 до 10. Она представляет собой квадратную таблицу, в которой числа от 1 до 10 располагаются в виде сетки. Горизонтально и вертикально числа увеличиваются от 1 до 10. Каждое число в таблице представлено в ячейке, образованной пересечением строки и столбца, причем значение ячейки соответствует произведению номера строки на номер столбца.

Таблица Пифагора имеет широкое применение в математике и образовании. Она помогает учащимся запомнить результаты умножения чисел от 1 до 10, а также понять основные принципы таблицы умножения. Благодаря наглядности и логическому расположению чисел, таблица Пифагора помогает визуализировать и запомнить математические факты.

Таблица Пифагора также является основой для изучения различных математических концепций и паттернов. Например, с помощью таблицы Пифагора можно легко определить парные числа, зеркальные числа и даже простые числа. Она также используется для решения различных математических задач, включая задачи на комбинаторику, теорию вероятностей и алгебру.

Таким образом, таблица Пифагора является не только удобным инструментом для запоминания и визуализации умножения чисел, но и мощным математическим инструментом, который может быть использован для решения различных задач и исследования математических паттернов.

Определение таблицы Пифагора

Таблица Пифагора представляет собой квадратную сетку, в которой каждая строка и каждый столбец соответствуют определенному числу. Первая строка и первый столбец содержат числа от 1 до 10 (или от 1 до 12), а внутри сетки каждая ячейка содержит произведение чисел, соответствующих номерам строки и столбца, на пересечении которых находится эта ячейка.

Таблица Пифагора используется для облегчения умножения чисел и помогает запомнить результаты умножения в удобной и наглядной форме. Например, если нужно найти произведение 6 и 8, можно найти число, соответствующее пересечению строки с числом 6 и столбца с числом 8 в таблице Пифагора – в данном случае это будет число 48.

Видео по теме:

Структура таблицы Пифагора

Заголовки строк и столбцов таблицы Пифагора содержат числа от 1 до n, которые обозначают множители. Первая строка и первый столбец являются заголовками и содержат эти числа.

Таблица Пифагора имеет симметричную структуру, что означает, что произведение чисел в ячейке с координатами (i, j) равно произведению чисел в ячейках с координатами (j, i). Таким образом, таблица Пифагора является квадратной, где размерность таблицы равна n.

Свойства таблицы Пифагора

1. Симметричность: Таблица Пифагора симметрична относительно главной диагонали, которая проходит от левого верхнего угла до правого нижнего угла. Это означает, что элементы в каждой строке и столбце повторяются в противоположном порядке. Например, элемент во второй строке и третьем столбце будет таким же, как элемент во втором столбце и третьей строке.

2. Простота и понятность: Таблица Пифагора является простым и понятным способом представления умножения чисел. Она позволяет быстро находить произведение любых двух чисел, просматривая соответствующие строку и столбец. Это особенно полезно для детей, которые только начинают изучать умножение.

3. Математические связи: Таблица Пифагора имеет много математических связей и зависимостей. Например, сумма чисел в каждой строке и столбце будет одинакова и равна произведению номера строки/столбца на сумму всех чисел от 1 до размера таблицы. Это свойство называется «геометрической прогрессией».

4. Практическое применение: Таблица Пифагора используется во множестве практических задач и областей, включая математику, физику, программирование и экономику. Она может помочь в решении задач по процентам, расчетам вероятности, нахождению наибольшего общего делителя и других математических операций.

Вывод: Таблица Пифагора является мощным инструментом, который помогает представить и использовать множество математических концепций. Ее свойства, такие как симметричность, простота и понятность, а также математические связи и практическое применение, делают ее важным элементом в образовании и решении задач.

Применение таблицы Пифагора

Основное применение таблицы Пифагора — это упрощение процесса умножения чисел. Благодаря ей, можно легко и быстро найти произведение двух чисел, находящихся в одной строке и столбце. Например, чтобы умножить 6 на 7, нужно найти пересечение строки с номером 6 и столбца с номером 7. В этой клетке будет находиться результат умножения чисел 6 и 7, то есть число 42.

Таблица Пифагора также может использоваться для нахождения делителей чисел. Для этого нужно найти число в таблице, которое делится на заданное число без остатка. Например, чтобы найти все делители числа 12, нужно найти все числа из таблицы Пифагора, которые делятся на 12 без остатка. В данном случае, это будут числа 1, 2, 3, 4, 6 и 12.

Таблица Пифагора также может быть полезна при решении задач по арифметике, математике и физике. Она может помочь в нахождении суммы, разности, произведения или частного чисел, а также в решении задач на пропорции и преобразование единиц измерения.

В общем, таблица Пифагора является очень полезным инструментом для упрощения процесса умножения и нахождения делителей чисел. Она помогает экономить время и усилия при выполнении различных математических операций и решении задач.

Учебные задачи с использованием таблицы Пифагора

Пример 1:

Найдите произведение чисел 7 и 9, используя таблицу Пифагора.

Из таблицы видно, что число 7 находится в левом столбце, а число 9 — в верхней строке. Таким образом, пересечение столбца 7 и строки 9 даст нам искомое произведение: 63.

Пример 2:

Найдите сумму чисел 4 и 5, используя таблицу Пифагора.

Из таблицы видно, что число 4 находится в левом столбце, а число 5 — в верхней строке. Таким образом, пересечение столбца 4 и строки 5 даст нам искомую сумму: 9.

Пример 3:

Найдите разность чисел 8 и 3, используя таблицу Пифагора.

Из таблицы видно, что число 8 находится в левом столбце, а число 3 — в верхней строке. Таким образом, пересечение столбца 8 и строки 3 даст нам искомую разность: 5.

Пример 4:

Найдите частное чисел 10 и 2, используя таблицу Пифагора.

Из таблицы видно, что число 10 находится в левом столбце, а число 2 — в верхней строке. Таким образом, пересечение столбца 10 и строки 2 даст нам искомое частное: 5.

Таким образом, таблица Пифагора может быть использована для решения различных задач, связанных с арифметическими операциями, такими как сложение, вычитание, умножение и деление.

Математические головоломки с таблицей Пифагора

Одна из самых популярных головоломок, связанных с таблицей Пифагора, — это задача о поиске недостающего числа. В этой головоломке представлена таблица Пифагора, в которой одно из чисел заменено на знак вопроса. Задача состоит в том, чтобы определить, какое число должно заменить знак вопроса, чтобы соблюсти закономерность умножения.

Например, в таблице Пифагора с замененным знаком вопроса:

• 1 2 3 4 5
• 2 4 6 ? 10
• 3 6 9 12 15
• 4 ? 12 16 20
• 5 10 15 20 25

Мы должны определить, что должно быть вместо знака вопроса. В данном случае, замененное число должно быть равно 8. Это можно определить, заметив, что замененное число является произведением номера строки и номера столбца, в которых оно находится.

Еще одна интересная головоломка, связанная с таблицей Пифагора, — это задача о поиске суммы чисел в определенной области таблицы. Например, в таблице Пифагора:

• 1 2 3 4 5
• 2 4 6 8 10
• 3 6 9 12 15
• 4 8 12 16 20
• 5 10 15 20 25

Задача может состоять в том, чтобы определить сумму всех чисел в прямоугольной области, ограниченной двумя заданными строками и двумя заданными столбцами. Например, если мы хотим найти сумму чисел в области, ограниченной строками 2 и 4 и столбцами 3 и 5, то сумма будет равна 9 + 12 + 15 + 20 + 25 = 81.

Такие головоломки способствуют развитию математического мышления, логики и аналитических навыков. Они также помогают улучшить умение применять таблицу Пифагора и находить закономерности в числах. Решение данных головоломок требует активного участия ума, поэтому их решение может быть интересным и увлекательным занятием для детей и взрослых.

Историческое значение таблицы Пифагора

Историческое значение таблицы Пифагора заключается в ее простоте и удобстве использования для обучения и запоминания таблицы умножения. Структура таблицы позволяет наглядно видеть взаимосвязь между числами и легко находить результаты умножения.

Таблица Пифагора была разработана в древности и использовалась для обучения детей в школах Пифагора, где математика имела особое значение. Она позволяла ученикам легко запоминать результаты умножения и быстро выполнять вычисления.

С течением времени таблица Пифагора стала широко распространена и использовалась в образовании по всему миру. Она является одним из основных инструментов для изучения и понимания умножения и математических операций.

Историческое значение таблицы Пифагора заключается в ее значимости для развития математики и образования. Она является важным инструментом для обучения и понимания математических операций, а также способом развития мышления и логического мышления у детей и взрослых.

Вопрос-ответ:

Что такое таблица Пифагора?

Таблица Пифагора — это математическая таблица, которая показывает произведение чисел от 1 до 10 в виде квадратной таблицы.

Как строится таблица Пифагора?

Таблица Пифагора строится путем умножения чисел от 1 до 10 друг на друга и расположения результатов в виде квадратной таблицы, где числа в строках и столбцах соответствуют множителям.

Как использовать таблицу Пифагора?

Таблица Пифагора используется для быстрого нахождения произведения двух чисел от 1 до 10. Для этого нужно найти соответствующую строку и столбец в таблице и найти пересечение, где будет указан результат.

Как читать таблицу Пифагора?

Чтение таблицы Пифагора осуществляется путем нахождения пересечения строки и столбца, соответствующих множителям. В этой ячейке будет указан результат умножения этих чисел.

В каких областях применяется таблица Пифагора?

Таблица Пифагора находит применение в различных областях, где требуется быстрое умножение чисел от 1 до 10, например, в школьной математике, при работе с пропорциями и преобразованиями, а также в программировании и инженерии.

Какая формула используется для построения таблицы Пифагора?

Формула для построения таблицы Пифагора имеет вид: a*b = c, где a и b — числа, а c — их произведение.

Как использовать таблицу Пифагора для умножения чисел?

Для умножения чисел с помощью таблицы Пифагора, находим нужное число в верхней строке и нужное число в левом столбце. Затем пересекаем эти два числа и получаем результат в ячейке, где они пересекаются.