Что такое теория в математике 5 класс

Теория в математике 5 класса — это совокупность основных правил, определений и законов, которые учащиеся изучают в этом классе. В данной статье рассматривается содержание и особенности теории в математике для учеников 5 класса, а также ее важность для дальнейшего обучения и понимания математики.

Теория в математике – это раздел математической науки, изучающий основы математического знания, его структуру и логические законы. В 5 классе ученики начинают изучение теории в математике, которая является основой для дальнейшего обучения и развития математического мышления.

Основные понятия теории в математике 5 класса включают в себя такие темы, как числа и числовые выражения, геометрия, алгебра, вероятность и статистика. Ученики учатся работать с числами, решать уравнения и неравенства, находить площади и объемы фигур, анализировать и интерпретировать данные в таблицах и диаграммах.

Принципы теории в математике 5 класса включают логическую последовательность, строгость и точность рассуждений, а также умение применять полученные знания на практике. Ученики учатся проводить доказательства, делать выводы и решать задачи, используя логические операции и математические операции.

Изучение теории в математике 5 класса помогает ученикам развивать абстрактное мышление, логику, аналитические и пространственные навыки. Это важная составляющая общего математического образования, которая поможет им справиться с более сложными математическими задачами в будущем.

Что такое теория в математике

Теория в математике включает в себя несколько основных понятий и принципов:

1. Определения: математические понятия, которые вводятся для описания и классификации объектов.
2. Аксиомы: независимые, основные, не доказываемые утверждения, на которых строится теория.
3. Теоремы: утверждения, которые можно доказать на основе аксиом и других теорем.
4. Доказательства: логический вывод, который позволяет установить истинность теорем на основе аксиом и других теорем.

Теория в математике позволяет строить логические цепочки утверждений и доказательств, что является основной особенностью математического подхода. Это позволяет математикам создавать новые теории, разрабатывать новые методы и решать сложные проблемы в различных областях науки и техники.

Теория в математике имеет широкое применение в решении практических задач, таких как моделирование процессов, доказательство алгоритмической сложности, криптография, оптимизация и другие области. Она также играет важную роль в формировании мышления, развитии логического и абстрактного мышления, а также в развитии аналитических и проблемно-ориентированных навыков.

Основные понятия

В математике существует ряд основных понятий, которые необходимо знать и понимать, чтобы успешно изучать теорию.

Понятие числа является основным в математике. Числа делятся на натуральные, целые, рациональные и иррациональные. Натуральные числа — это числа, с которыми мы сталкиваемся ежедневно: 1, 2, 3 и так далее. Целые числа включают в себя натуральные числа и их отрицания: -1, -2, -3 и так далее. Рациональные числа — это числа, которые можно представить в виде дроби, например, 1/2 или 3/4. Иррациональные числа — это числа, которые не могут быть представлены в виде дроби, например, корень из 2.

Понятие операции также является важным. Операции включают сложение, вычитание, умножение и деление. Сложение — это объединение двух чисел в одно, вычитание — это нахождение разности между двумя числами, умножение — это повторение числа несколько раз, а деление — это разделение числа на другое число.

Также в математике есть понятие уравнения. Уравнение — это математическое выражение, в котором две величины сравниваются. Оно состоит из левой и правой частей, разделенных знаком равенства. Решение уравнения — это значение переменной, при котором обе его части становятся равными.

Важным понятием является также понятие функции. Функция — это отображение одного множества в другое. В математике функции обозначаются буквой f и записываются в виде f(x), где x — входное значение, а f(x) — выходное значение.

Это лишь некоторые из основных понятий, которые необходимо знать для изучения теории в математике.

Аксиомы

В математике аксиомы представляют собой основные правила и свойства, которые считаются истинными без доказательства. Они определяют базовые понятия и отношения в данной теории, а также устанавливают правила операций и преобразований.

Аксиомы часто выражаются с помощью логических утверждений, которые могут быть выражены в виде формул или предложений. Некоторые известные аксиомы включают аксиомы Пеано, аксиомы Планка, аксиомы геометрии Евклида и многие другие.

Аксиомы являются фундаментальным и неотъемлемым компонентом математической теории, обеспечивая ее консистентность и стройность. Они служат основой для построения математических моделей и решения различных задач в рамках данной теории.

Теоремы

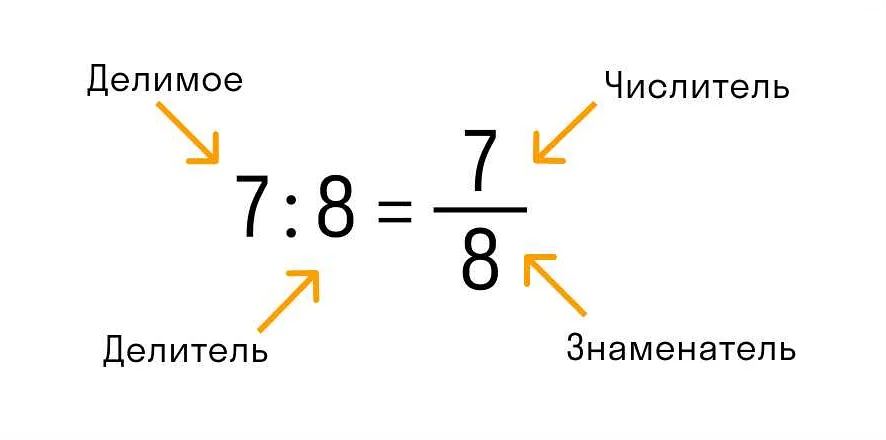
Теоремы имеют особое значение в математике, так как они позволяют выводить новые факты из уже известных. Доказательство теоремы основывается на применении логических законов и математических операций.

Пример: Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов: a2 + b2 = c2.

Доказательство теоремы Пифагора включает использование геометрических фигур, арифметических операций и алгебраических преобразований.

Теоремы играют важную роль в математике, так как они позволяют систематизировать и упорядочить знания, а также строить новые математические конструкции и развивать науку.

Принципы теории

Теория в математике основана на нескольких принципах, которые помогают понять и объяснить различные математические концепции. Вот некоторые из них:

1. Принцип непротиворечивости: Теория должна быть свободна от противоречий. Все ее утверждения должны быть логически согласованы и не мешать друг другу.
2. Принцип полноты: Теория должна охватывать все возможные случаи и ситуации. Ни один важный аспект не должен быть пропущен или игнорирован.
3. Принцип конкретности: Теория должна быть ясной и конкретной, чтобы быть понятной и применимой в практических задачах.
4. Принцип доказательности: Теория должна быть основана на строгих математических доказательствах. Все ее утверждения должны быть логически обоснованы и проверены.
5. Принцип независимости: Теория должна быть независимой от конкретной практической ситуации. Она должна иметь общую применимость и применима к различным областям и задачам.

Соблюдение этих принципов помогает математикам разрабатывать и использовать теории, которые являются надежными и эффективными инструментами для решения математических задач и понимания мира вокруг нас.

Доказательство

В математическом доказательстве используются различные методы, такие как прямое доказательство, доказательство от противного, математическая индукция и т.д. В зависимости от ситуации и задачи выбирается наиболее подходящий метод доказательства.

Доказательство состоит из нескольких основных элементов:

ЭлементОписание

Гипотеза	Начальное предположение, которое считается истинным.
Логические шаги	Последовательность логических операций, которые приводят к выводу.
Вывод	Конечное утверждение, которое является результатом доказательства.

Важной частью доказательства является ясное и последовательное изложение каждого шага, чтобы другие ученые или математики могли легко проверить его. Доказательство должно быть строго логичным и не допускать ошибок или противоречий.

Доказательство играет важную роль в математике, поскольку позволяет устанавливать истинность утверждений и строить новые теории на основе уже известных фактов. Оно также помогает развивать логическое мышление и аналитические навыки учащихся.

Обратная задача

Обратные задачи широко применяются в различных областях математики. Например, в геометрии обратная задача может быть связана с определением исходных размеров объекта, исходя из его изображения или геометрических свойств. В алгебре обратная задача может быть связана с определением исходных значений переменных, исходя из заданного уравнения или системы уравнений.

Решение обратной задачи требует анализа и использования различных методов и подходов. Часто требуется применение математического моделирования, алгоритмических методов и численных методов, чтобы найти правильное решение.

Обратные задачи имеют практическое применение во многих областях, таких как физика, экономика, инженерия и многие другие. Они позволяют установить исходные условия или параметры, исходя из известных результатов или наблюдений.

Вопрос-ответ:

Какие основные понятия входят в теорию в математике для 5 класса?

Основные понятия в теории математики для 5 класса включают в себя такие понятия, как число, операции сложения, вычитания, умножения и деления, пропорции, геометрические фигуры, периметр и площадь, а также решение простых уравнений.

Что такое число в математике для 5 класса?

В математике для 5 класса число — это абстрактный объект, который используется для измерения и подсчета. В этом классе основное внимание уделяется натуральным числам (1, 2, 3, …), целым числам (…, -3, -2, -1, 0, 1, 2, 3, …), а также простым дробям и десятичным дробям.

Какие принципы важны в теории математики для 5 класса?

В теории математики для 5 класса важно следовать таким принципам, как принцип единства и разности, принцип сохранения числа, принцип симметрии, принцип равенства, принцип замены, принцип ассоциативности и коммутативности операций, а также принцип учета знака при операциях сложения и вычитания.

Какие геометрические фигуры изучаются в теории математики для 5 класса?

В теории математики для 5 класса изучаются такие геометрические фигуры, как треугольник, прямоугольник, квадрат, параллелограмм, ромб, трапеция, круг и эллипс. Для каждой фигуры изучаются ее основные свойства, такие как количество сторон, углов, длина сторон, радиусы и диаметры.

Видео по теме: