Что называют выражением в математике

Выражение в математике – это математическое выражение, состоящее из чисел, переменных, операций и математических символов. Оно может быть простым или сложным, и представляет собой формулу, которую можно вычислить для получения численного значения. Выражения используются во многих областях математики, физики и других наук для описания и решения различных задач и проблем.

В математике выражение – это математическое выражение, состоящее из чисел, переменных и операторов, связанных между собой. Оно представляет собой комбинацию символов, которая может быть вычислена, чтобы получить численное значение. Выражения используются для описания различных математических операций и решения уравнений.

Выражения могут содержать различные математические операторы, такие как сложение, вычитание, умножение и деление, а также скобки, которые указывают порядок выполнения операций. Они могут также включать функции, логические операторы и другие математические конструкции.

Примеры выражений в математике включают: «2 + 3», «5 * (7 — 2)», «x + y», «sin(x) + cos(y)». Каждое из этих выражений может быть вычислено, чтобы получить численное значение или новое выражение.

Особенностью выражений в математике является то, что они могут быть использованы для решения различных математических задач и применены в различных областях науки и техники. Они являются основой для работы с числами и переменными и позволяют нам описывать и анализировать различные математические явления и законы.

В итоге, выражение в математике является основным строительным блоком для решения математических задач и проведения аналитических исследований. Оно представляет собой комбинацию чисел, переменных и операторов, которую можно вычислить для получения численного значения или нового выражения.

Определение выражения в математике

Выражение в математике представляет собой комбинацию чисел, переменных и операций, объединенных вместе. Оно может содержать одну или несколько переменных, а также математические операции, такие как сложение, вычитание, умножение и деление.

Выражение может быть простым, состоящим из одного числа или переменной, или составным, когда в него входят несколько чисел, переменных и операций. Примеры простых выражений включают «5», «x» и «2y». Примеры составных выражений включают «3x + 2y», «4(x + 2)» и «2x^2 — 3xy + 5».

Выражения в математике могут быть использованы для решения уравнений, нахождения значений функций или выполнения других математических операций. Они играют важную роль в алгебре и математическом анализе, позволяя нам выразить и манипулировать математическими отношениями и операциями.

Кроме того, выражения в математике могут содержать скобки, которые позволяют указать порядок выполнения операций. Например, в выражении «3(x + 2)» скобки указывают, что сначала нужно выполнить операцию внутри скобок (сложение), а затем умножить результат на 3.

Примеры выражений в математике

В математике выражение представляет собой комбинацию чисел, переменных, операций и скобок. Оно может содержать как простые, так и сложные выражения. Вот несколько примеров выражений:

ПримерОписание

3 + 5	Простое выражение, состоящее из двух чисел и операции сложения
x — 2	Выражение с переменной x и операцией вычитания
(a + b) * c	Выражение с использованием скобок и операции умножения
4 / (2 + 1)	Сложное выражение с использованием скобок и операции деления
2^3	Выражение с использованием операции возведения в степень

Это лишь несколько примеров выражений в математике. Выражения могут быть намного сложнее и содержать больше операций, переменных и скобок. Использование выражений позволяет проводить различные вычисления и решать математические задачи.

Особенности выражений в математике

Выражение в математике представляет собой математическое выражение, состоящее из чисел, переменных, операций и скобок. Оно может быть использовано для вычисления значений, решения уравнений и выполнения различных математических операций.

Вот некоторые особенности выражений в математике:

1. Операции: Выражения могут содержать различные математические операции, такие как сложение, вычитание, умножение и деление. Операции могут быть обозначены символами, такими как «+», «-«, «*», «/».
2. Переменные: Выражения могут содержать переменные, которые представляют неизвестные значения. Переменные могут быть обозначены буквами или другими символами.
3. Числа: Выражения могут содержать числа, которые представляют известные значения. Числа могут быть целыми, десятичными или дробными.
4. Скобки: Выражения могут содержать скобки, которые используются для определения порядка выполнения операций. Скобки могут быть круглыми, квадратными или фигурными.
5. Порядок выполнения операций: При вычислении выражений важно учитывать порядок выполнения операций. Например, умножение и деление выполняются перед сложением и вычитанием.

Выражения в математике используются для решения различных задач, таких как нахождение значений функций, вычисление площадей и объемов, решение уравнений и многое другое. Понимание особенностей выражений поможет вам использовать их эффективно в решении математических задач.

Как составить выражение в математике

Для того чтобы составить выражение, следует учитывать следующие особенности:

1. Определить числа, которые будут использоваться в выражении. Числа могут быть целыми, десятичными, положительными или отрицательными.
2. Выбрать операции, которые будут применяться к числам. Операции могут быть сложением, вычитанием, умножением, делением и другими математическими операциями.
3. Определить порядок выполнения операций. В математике есть определенные правила порядка, которые указывают, какие операции нужно выполнить первыми.

Примеры выражений:

• Выражение 1: 5 + 3 * 2
• Выражение 2: (4 — 2) / 3
• Выражение 3: 2 * (6 + 4) — 8

В выражении 1 сначала выполняется умножение, затем сложение. В выражении 2 сначала выполняется вычитание, затем деление. В выражении 3 сначала выполняется сложение в скобках, затем умножение, и в конце вычитание.

Составление выражений в математике требует внимательности и точности. Неправильный порядок операций может привести к неверному результату. Поэтому важно внимательно следовать правилам математики при составлении выражений.

Ключевые элементы выражений в математике

Числа: в выражениях можно использовать как натуральные числа (1, 2, 3 и т.д.), так и дроби, отрицательные числа, числа с плавающей точкой и другие математические константы, такие как π или e.

Переменные: переменные в выражениях представляют неизвестные значения или значения, которые могут меняться. Обычно переменные обозначаются буквами, например, x или y.

Операции: операции в выражениях выполняют различные математические действия над числами и переменными. Некоторые основные операции включают сложение (+), вычитание (-), умножение (*), деление (/), возведение в степень (^) и извлечение квадратного корня (sqrt).

Скобки: скобки используются для группировки элементов выражений и для указания порядка выполнения операций. Наиболее распространенные типы скобок — круглые скобки (()), квадратные скобки ([]) и фигурные скобки ({}).

Примеры: примерами выражений могут быть:

3 + 5 * 2 — в данном выражении сначала выполняется умножение (5 * 2), затем сложение (3 + 10), результатом является число 13.

(4 + 7) / 2 — в данном выражении сначала выполняется сложение (4 + 7), затем деление (11 / 2), результатом является число 5.5.

x^2 + 2 * x + 1 — в данном выражении переменная x возводится в квадрат (x^2), затем происходит умножение (2 * x), и в конце складываются все элементы выражения, результатом является выражение в зависимости от значения переменной x.

Понимание ключевых элементов выражений позволяет более точно и эффективно решать математические задачи, а также анализировать их результаты.

Различия между выражением и уравнением

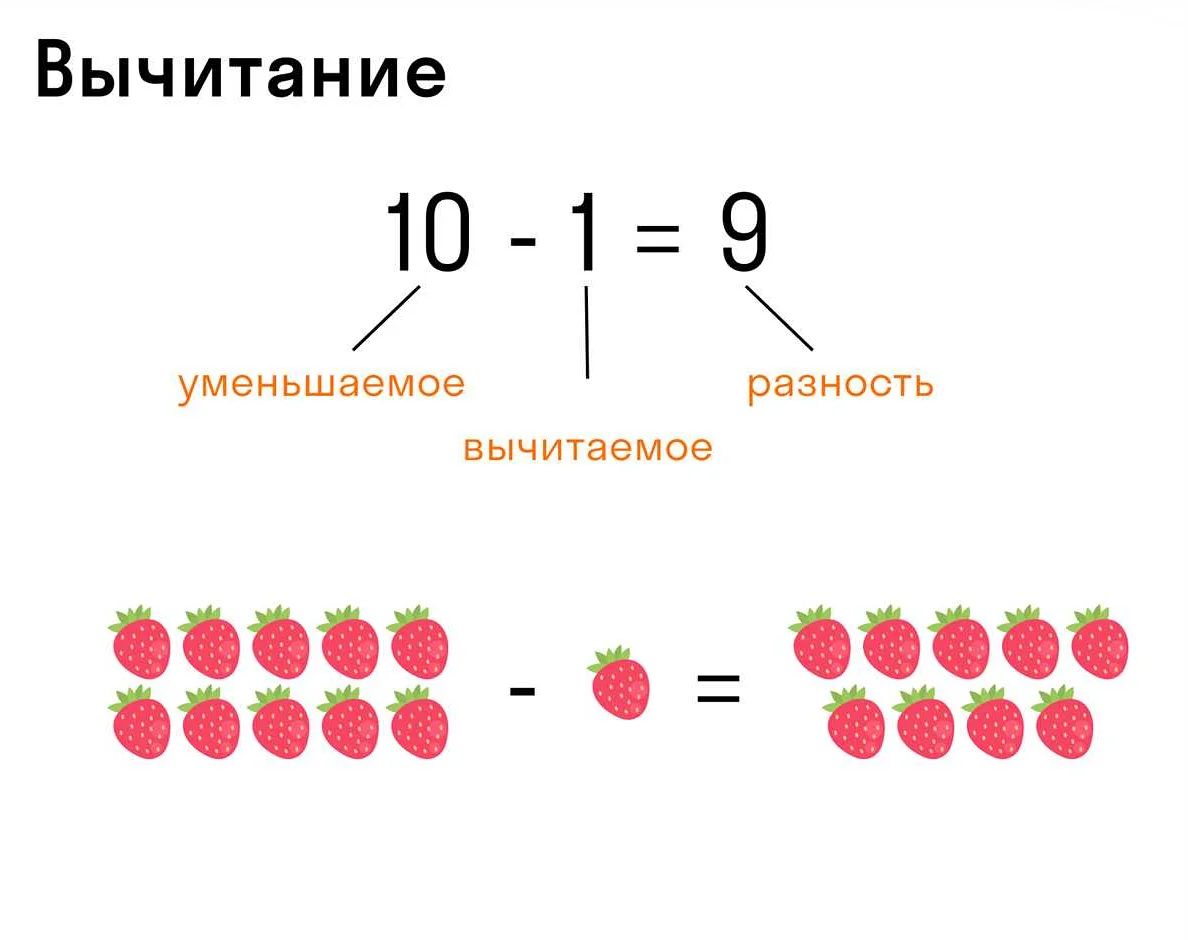
Выражение — это математическая конструкция, состоящая из чисел, переменных, операций и функций. В выражении может быть использовано одно или несколько чисел, а также символы операций, такие как сложение, вычитание, умножение и деление. Примеры выражений: 2 + 3, 4x + 5y, sqrt(9).

Уравнение — это математическое равенство, в котором присутствуют переменные и знак равенства. Уравнение позволяет нам найти значение или значения переменной, которые удовлетворяют равенству. Примеры уравнений: 2x + 3 = 7, x^2 — 9 = 0, 3y — 2 = 4y + 1.

Основное различие между выражением и уравнением заключается в том, что выражение не содержит знака равенства и не может быть решено. Выражение может быть упрощено или вычислено, но оно не может быть решено, так как оно не содержит переменных. В то же время, уравнение всегда содержит знак равенства и может быть решено, чтобы найти значение переменной или значения, которые удовлетворяют равенству.

Таким образом, выражение и уравнение представляют разные математические конструкции, которые часто используются вместе, но имеют свои собственные особенности и цели в математике.

Значение выражения в математике

Выражения могут быть простыми или сложными. Простое выражение состоит из одного числа или одной переменной. Например, выражение «5» или «x». Сложное выражение состоит из нескольких чисел, переменных и операторов, объединенных в определенном порядке. Например, выражение «3 + 2 * x».

Чтобы вычислить значение выражения, необходимо знать значения переменных и выполнять операции в соответствии с математическими правилами. Например, для выражения «3 + 2 * x», если известно, что x = 4, его значение можно вычислить следующим образом: 3 + 2 * 4 = 3 + 8 = 11.

Значение выражения может быть числом, переменной, функцией или другим математическим объектом. Например, выражение «5» имеет значение 5, выражение «x» имеет значение переменной x, выражение «sin(x)» имеет значение синуса переменной x.

Выражения используются в математике для описания и решения различных задач. Они позволяют выразить математические отношения, формулы и уравнения. Значение выражения позволяет получить конкретный результат и сделать выводы о заданной математической задаче.

В таблице ниже приведены примеры различных выражений и их значений:

ВыражениеЗначение

2 + 3	5
4 * 5	20
x + 2	зависит от значения переменной x
sin(0)	0

Важность изучения выражений в математике

Изучение выражений в математике играет ключевую роль в развитии логического и аналитического мышления у учащихся.

Основная цель изучения выражений заключается в том, чтобы научить студентов правильно формулировать и решать математические задачи. Знание основных правил и принципов работы с выражениями помогает учащимся понять, как работает математическая логика и как применять ее для решения сложных задач.

Изучение выражений также помогает учащимся развивать навыки анализа и критического мышления. Они учатся анализировать и оценивать информацию, применять логические законы и принципы для аргументации и выводов.

Важность изучения выражений проявляется и в повседневной жизни. Знание и понимание основных математических выражений позволяет людям лучше ориентироваться в различных ситуациях, связанных с финансовыми операциями, планированием расходов и другими аспектами повседневной жизни.

Таким образом, изучение выражений в математике имеет не только академическую ценность, но и практическую пользу, помогая учащимся развивать ключевые навыки и умения, необходимые для успешной жизни и карьеры.

Видео по теме:

Что такое выражение в математике?

Выражение в математике — это комбинация чисел, переменных и математических операций. Оно может быть записано в виде формулы или алгебраического выражения. Например, выражение «2x + 5» содержит переменную x, числа 2 и 5, а также операции умножения и сложения.

Что такое выражение в математике?

Выражение в математике — это комбинация чисел, переменных, операций и знаков, объединенных вместе. Оно может содержать как числа и переменные, так и арифметические операции, такие как сложение, вычитание, умножение и деление. Выражение может быть как простым, состоящим из одного числа или переменной, так и сложным, включающим несколько операций.