Что такое задачи в математике

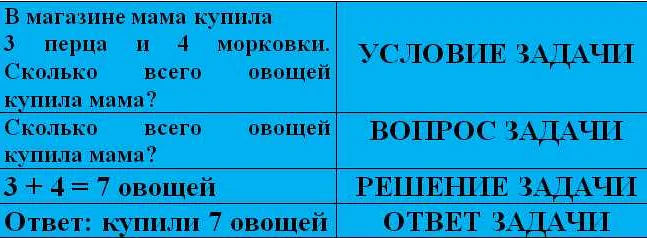
Задачи в математике — это математические задания, которые требуют решения с использованием различных методов и техник. Они помогают развивать логическое мышление, аналитические навыки и способность применять математические знания на практике. В статье мы рассмотрим различные типы задач в математике и подробно изучим основные методы и стратегии их решения.

Математика — это наука, которая изучает свойства и взаимоотношения чисел, форм, пространств и структур. Одним из важных аспектов математики является решение задач. Задача в математике — это проблема, требующая нахождения определенного решения с использованием математических методов и инструментов.

Задачи в математике могут быть различных видов. Они могут быть алгебраическими, геометрическими, вероятностными, комбинаторными и т. д. Каждый вид задачи требует своего подхода и метода решения. Некоторые задачи могут иметь одно решение, в то время как другие могут иметь несколько возможных решений.

Пример: Решите уравнение: 2x + 5 = 15

Для решения задач в математике можно использовать различные методы, такие как алгебраические преобразования, графический анализ, использование формул и т. д. Важно уметь анализировать задачу, выделять в ней важные данные и определить неизвестные величины, которые нужно найти.

Решение задач в математике развивает логическое мышление, абстрактное мышление и умение применять математические методы для решения реальных проблем. При этом важно уметь аргументировать свои решения и проверять их на корректность.

Задачи в математике: определение, виды и решение

Задачи в математике могут иметь разные виды и классифицироваться по различным критериям. Одним из основных критериев является степень сложности задачи. В зависимости от уровня сложности, задачи могут быть разделены на простые, средней сложности и сложные.

Простые задачи в математике обычно решаются с помощью элементарных операций, таких как сложение, вычитание, умножение и деление. Они требуют небольшого количества шагов и являются хорошим началом для начинающих учеников.

Задачи средней сложности включают в себя более сложные математические операции, такие как возведение в степень, извлечение корня, решение уравнений и т.д. Они требуют более глубокого понимания математических концепций и навыков и могут быть более требовательными для учеников.

Сложные задачи в математике представляют собой более сложные проблемы, которые требуют применения продвинутых математических методов и техник. Они могут быть связаны с теорией чисел, геометрией, алгеброй или другими разделами математики. Решение сложных задач обычно требует более глубокого понимания материала и более высокого уровня навыков.

Задачи в математике могут также классифицироваться по содержанию. Некоторые распространенные типы задач включают задачи на нахождение неизвестных величин, задачи на определение условий равенства, задачи на построение графиков, задачи на нахождение максимального или минимального значения и другие.

Решение задач в математике включает в себя анализ условия задачи, построение математической модели, решение полученных уравнений или неравенств, проверку полученного результата и формулировку окончательного ответа.

В заключение, задачи в математике являются важной частью математического образования и помогают развить ученикам не только математические навыки, но и способность анализировать проблемы и находить решения.

Видео по теме:

Определение задач в математике

Задачи в математике могут быть представлены в различных форматах, таких как текстовые задачи, графические задачи, символические задачи или комбинированные задачи, но в целом они имеют общую цель — найти решение, определить значение или ответ на поставленный вопрос.

Задачи в математике могут быть как простыми, с небольшим количеством операций и шагов для решения, так и сложными, требующими применения различных математических концепций, теорем и методов.

Основная цель решения задач в математике — развить навыки логического мышления, аналитического мышления и применения математических знаний для решения реальных проблем и задач.

Решение задач в математике может включать различные шаги, такие как анализ условия задачи, построение математической модели, применение соответствующих методов и алгоритмов, выполнение вычислений и проверка полученных результатов.

В целом, задачи в математике способствуют развитию математической интуиции, логического мышления, творческого мышления и способности к абстрактному мышлению, что является важными навыками для применения математики в реальной жизни и в других областях знания.

Виды задач в математике

Задачи в математике могут быть различной природы и характеризуются своими особенностями и спецификой решения. В зависимости от постановки и целей решения, задачи в математике можно разделить на несколько типов:

1. Аналитические задачи – это задачи, в которых требуется провести анализ и исследование заданного объекта или явления, используя математические методы и инструменты. В ходе решения аналитической задачи необходимо выявить связи и закономерности, сделать выводы и сформулировать результат.
2. Геометрические задачи – это задачи, связанные с изучением геометрических фигур, пространственных объектов и их свойств. Решение геометрических задач требует использования геометрических принципов, теорем и формул.
3. Алгебраические задачи – это задачи, в которых используются алгебраические операции, формулы и уравнения для решения задачи. В ходе решения алгебраической задачи необходимо выполнять различные алгебраические преобразования и операции с числами и переменными.
4. Статистические задачи – это задачи, связанные с обработкой и анализом статистических данных и информации. Решение статистической задачи требует использования методов статистики, вероятности и теории чисел.
5. Оптимизационные задачи – это задачи, связанные с нахождением оптимальных значений и решений с учетом определенных условий и ограничений. Решение оптимизационной задачи включает поиск максимума или минимума определенной функции или величины.

Каждый вид задач в математике имеет свои особенности и требует применения соответствующих математических методов и инструментов для их решения.

Вопрос-ответ:

Какие бывают виды задач в математике?

В математике существует несколько видов задач: арифметические задачи, геометрические задачи, алгебраические задачи, задачи на нахождение вероятности и задачи на оптимизацию.

Что такое задачи на нахождение вероятности?

Задачи на нахождение вероятности — это задачи, в которых требуется определить вероятность наступления определенного события. Например, задача о бросании монеты, где нужно найти вероятность выпадения орла или решки.

Как решать арифметические задачи?

Арифметические задачи решаются путем применения арифметических операций: сложение, вычитание, умножение и деление. Необходимо внимательно прочитать условие задачи, выделить из него важные данные и использовать соответствующую операцию для нахождения ответа.

Что такое задачи на оптимизацию?

Задачи на оптимизацию — это задачи, в которых требуется найти наилучшее решение среди всех возможных вариантов. Например, задача о нахождении максимального значения функции или задача о минимизации затрат при заданных условиях.

Какие есть способы решения геометрических задач?

Существует несколько способов решения геометрических задач. Один из них — использование геометрических фигур и их свойств для построения доказательств и нахождения ответов. Другой способ — использование алгебраических методов, например, систем уравнений или формул для нахождения длин сторон и углов.

Решение задач в математике

Во время решения математической задачи необходимо следовать определенной последовательности действий:

1. Чтение и понимание условия задачи: необходимо внимательно прочитать и понять условие задачи, выделить главные данные и искомое значение.
2. Составление плана решения: на основе условия задачи и доступных данных нужно разработать план действий, определить, какими формулами или методами математики можно воспользоваться для решения.
3. Вычисление и анализ данных: используя ранее разработанный план, следует провести вычисления и анализировать полученные результаты.
4. Проверка ответа: после проведения всех вычислений необходимо проверить полученный ответ на соответствие условию задачи и заданной точности.
5. Представление решения: окончательный ответ следует представить в виде полного и понятного математического решения, с указанием всех промежуточных шагов и объяснений.

Решение задач в математике требует тщательности, логического мышления и умения применять различные математические концепции и методы. Оно позволяет развивать навыки анализа, рассуждения, абстрактного мышления и применения математического знания на практике.

Алгебраические задачи в математике

В алгебраических задачах часто используются переменные, которые представляют неизвестные значения. Задачи могут быть различными по своей природе, но общая идея заключается в нахождении соотношений между переменными и решении системы уравнений для определения неизвестных значений.

Примеры алгебраических задач включают в себя нахождение значений переменных в уравнениях, решение систем уравнений, расчеты с переменными и выполнение операций с алгебраическими выражениями.

Решение алгебраических задач может включать следующие шаги:

1. Запись задачи в виде уравнений или системы уравнений.
2. Преобразование и упрощение уравнений с использованием алгебраических методов и правил.
3. Решение уравнений для определения значений переменных.
4. Проверка решения путем подстановки найденных значений переменных в исходные уравнения.

Алгебраические задачи имеют широкое применение в различных областях науки и повседневной жизни. Они помогают анализировать и решать проблемы, моделировать физические и экономические процессы, а также разрабатывать математические модели для прогнозирования и оптимизации.

Важно уметь разбираться в алгебраических задачах, так как они являются основой для изучения более сложных математических тем и дисциплин, таких как аналитическая геометрия, математический анализ и теория вероятностей.

Геометрические задачи в математике

Такие задачи могут включать построение геометрических фигур, определение их свойств, вычисление площадей и объемов, а также нахождение геометрических параметров, таких как длины, углы и расстояния.

Для решения геометрических задач необходимо использовать знания о геометрических фигурах, их свойствах и взаимосвязях. Также важно уметь применять различные геометрические теоремы и правила.

Решение геометрической задачи обычно состоит из нескольких этапов. Сначала необходимо понять условие задачи и определить, какие данные даны и что требуется найти. Затем следует проанализировать геометрические фигуры, использовать известные свойства и теоремы для нахождения решения. Наконец, результат необходимо проверить и сформулировать окончательный ответ.

Геометрические задачи могут быть как простыми, так и сложными. Они могут включать в себя различные элементы геометрии, такие как прямые, окружности, треугольники, многоугольники и т.д. Решение задач может потребовать применения таких понятий, как сходство фигур, теорема Пифагора, теорема синусов и косинусов и другие.

Геометрические задачи являются важной частью математического образования и имеют широкое применение в реальной жизни. Они позволяют развивать навыки анализа и решения проблем, а также улучшают понимание геометрических принципов и их применение в реальных ситуациях.

Задачи на вероятность в математике

В задачах на вероятность необходимо определить вероятность возникновения определенного события или вычислить вероятность комбинации нескольких событий. Задачи могут быть различного уровня сложности и требовать разных математических подходов для их решения.

Одним из типов задач на вероятность является задача о броске монеты. Например, в задаче может быть дано следующее условие: «Какова вероятность выпадения орла при однократном броске симметричной монеты?» Для решения этой задачи необходимо учесть, что монета имеет две стороны – орел и решка, и обе стороны равновероятны. Таким образом, вероятность выпадения орла будет равна 0,5 или 50%.

Другим типом задач на вероятность являются задачи о выборе шаров из урны. В таких задачах может быть дано условие, например: «В урне находится 5 зеленых шаров и 3 красных шара. Какова вероятность выбора зеленого шара при случайном извлечении одного шара из урны?» Для решения этой задачи необходимо учесть, что вероятность выбора зеленого шара будет равна отношению количества зеленых шаров к общему количеству шаров, то есть 5/8 или 0,625.

Задачи на вероятность могут быть сложнее и включать комбинаторику. Например, задача о выборе комитета из группы людей. В такой задаче может быть дано условие: «Из группы из 10 человек нужно выбрать комитет из 3-х человек. Какова вероятность того, что в комитете будут два мужчины и одна женщина?» Для решения этой задачи необходимо использовать комбинаторные формулы и учитывать, что вероятность выбора одного события зависит от количества возможных вариантов.

Таким образом, задачи на вероятность в математике позволяют применить знания о вероятности и комбинаторике для решения различных практических задач. Решение таких задач требует точности и логического мышления, а также умения применять математические формулы и концепции.

Задачи на математическую логику

Такие задачи помогают развивать логическое мышление, аналитические навыки, умение абстрагироваться от конкретной ситуации и находить общие закономерности.

Примеры задач на математическую логику:

1. Задачи на поиск закономерности в последовательности чисел.
2. Задачи на определение логического следствия.
3. Задачи на использование логических связок (и, или, не).
4. Задачи на построение логических схем.
5. Задачи на использование логических законов (закон де Моргана, закон исключенного третьего и др.).

Решение таких задач может потребовать применения различных методов: анализа, индукции, дедукции, построения таблиц истинности и т. д.

Задачи на математическую логику могут встречаться как в школьной программе, так и в профессиональной деятельности, особенно в области информатики и программирования.

Практическое применение задач в математике

Задачи в математике имеют не только теоретическое значение, но и широкое практическое применение в различных областях жизни. Они помогают нам развивать логическое мышление, учат решать сложные задачи, а также дают нам навыки применения математических знаний на практике.

Одно из практических применений математических задач — это в области финансов. Знание математики позволяет нам рассчитывать проценты, сумму инвестиций, доходность различных финансовых инструментов и т.д. Без математических навыков мы были бы неспособны принимать рациональные финансовые решения и планировать свои финансовые потоки.

Еще одной областью, где задачи в математике имеют практическое применение, является технические науки. Здесь математика используется для решения различных инженерных задач, например, при расчете конструкций, оптимизации работы систем, моделирования и прогнозирования процессов. Математические модели позволяют нам более точно предсказывать результаты и делать правильные технические решения.

Также задачи в математике находят свое применение в науке. Математические модели используются для описания различных физических, химических и биологических процессов. Они помогают нам понять и объяснить сложные явления и законы природы. Без математических знаний мы бы не смогли сделать многие открытия и вывести новые научные результаты.

В целом, задачи в математике имеют широкое практическое применение в различных областях жизни. Они помогают нам решать сложные проблемы, принимать рациональные решения и понимать мир вокруг нас.