На сколько больше что значит в математике

Узнайте, как определить, насколько одно число больше другого в математике. Узнайте, как использовать различные методы и формулы для вычисления разницы между числами и понять, насколько одно число превосходит другое.

Математика — это наука, которая изучает структуру, свойства и взаимоотношения чисел, пространства и форм. В математике мы часто сталкиваемся с таким понятием, как «на сколько больше». Но что оно значит на самом деле? Давайте разберемся.

Когда говорят, что одно число «на сколько-то больше» другого, это означает, что разница между этими числами равна указанной величине. Например, если сказать, что число 10 «на 5 больше» числа 5, это означает, что разница между ними равна 5.

Важно помнить, что «на сколько больше» является относительным понятием. Это значит, что результат будет зависеть от чисел, с которыми мы сравниваем. Например, если сказать, что число 10 «на 5 больше» числа 5, это верно. Но если сравнить число 10 с числом 15, то оно будет «на 5 меньше» числа 15.

В математике есть определенные методы для вычисления разности двух чисел и определения, на сколько одно число больше или меньше другого. Используя эти методы, мы можем более точно определить, на сколько больше или меньше одно число по сравнению с другим.

Математика: базовые понятия

В математике существуют базовые понятия, которые являются основой для дальнейшего изучения этой науки:

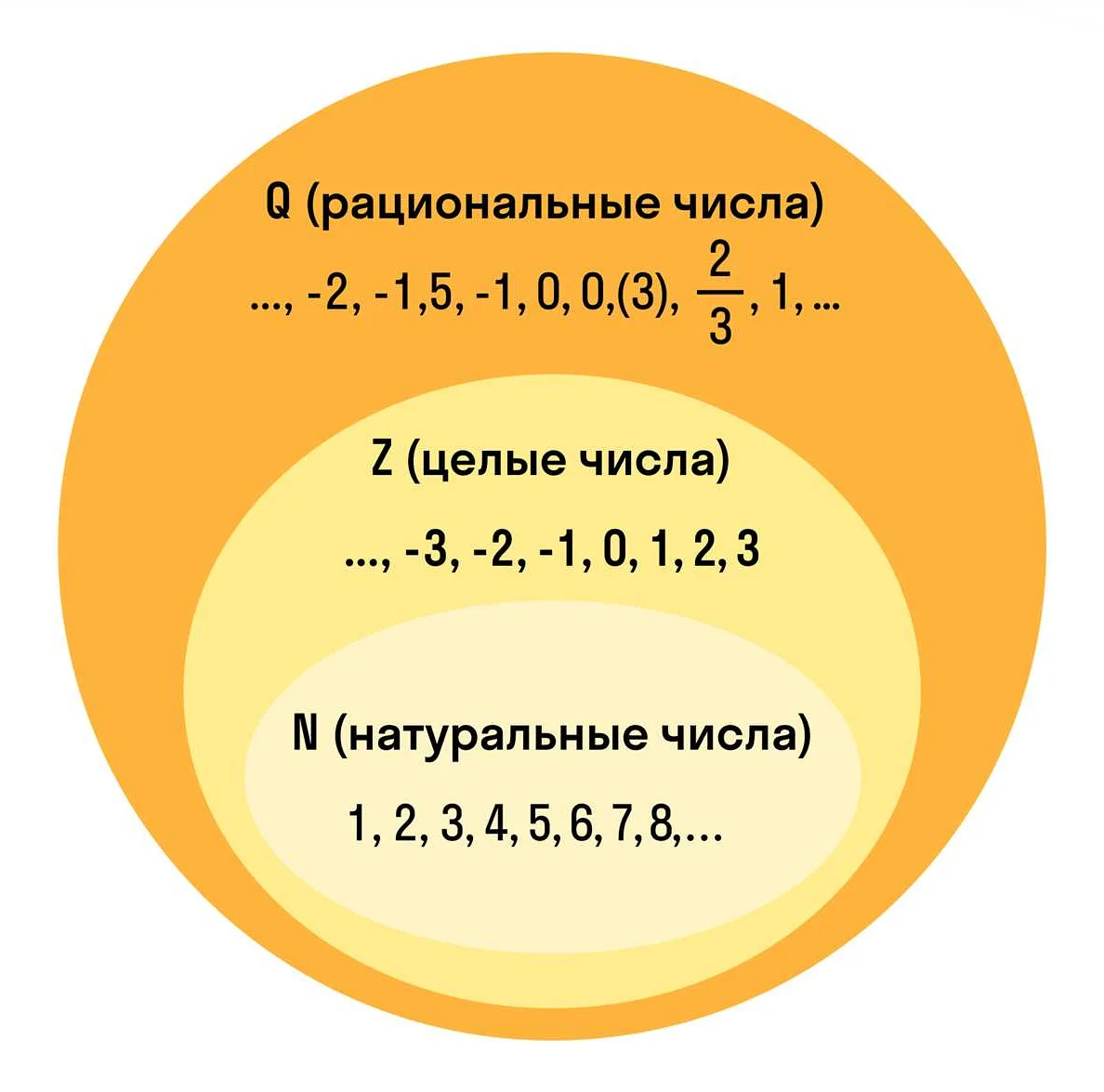
Числа: Математика основана на числах. Числа могут быть натуральными (1, 2, 3…), целыми (-3, -2, -1, 0, 1, 2, 3…), рациональными (дроби) или иррациональными (как, например, число пи).

Операции: Операции — это действия, которые можно выполнить с числами. Основные операции в математике — сложение, вычитание, умножение и деление.

Формулы: Формулы — это математические выражения, которые содержат переменные и операторы. Формулы позволяют решать математические задачи и находить значения неизвестных величин.

Уравнения: Уравнения — это математические выражения, которые утверждают, что два выражения равны. Решение уравнений позволяет найти значения переменных, при которых уравнение выполняется.

Геометрия: Геометрия изучает формы, размеры и свойства фигур в пространстве. Она включает в себя такие понятия, как линии, углы, треугольники, круги и многое другое.

Вероятность: Вероятность — это раздел математики, который изучает случайные явления и вероятность их возникновения. Вероятность позволяет оценивать шансы на события и принимать рациональные решения на основе этой информации.

Статистика: Статистика — это наука, которая собирает, анализирует и интерпретирует данные. Статистика позволяет делать выводы на основе имеющихся данных и прогнозировать будущие события.

Алгебра: Алгебра — это раздел математики, который изучает алгебраические структуры и их свойства. Алгебра позволяет решать уравнения, работать с формулами и проводить анализ функций.

Тригонометрия: Тригонометрия — это раздел математики, который изучает отношения между углами и сторонами треугольников. Она находит применение в геометрии, физике и других науках.

Понимание этих базовых понятий поможет в освоении более сложных математических концепций и решении задач в различных областях знания и деятельности.

Арифметика: основы

Сложение — это операция, при которой два числа объединяются в одно число. Например, при сложении чисел 2 и 3 получается число 5.

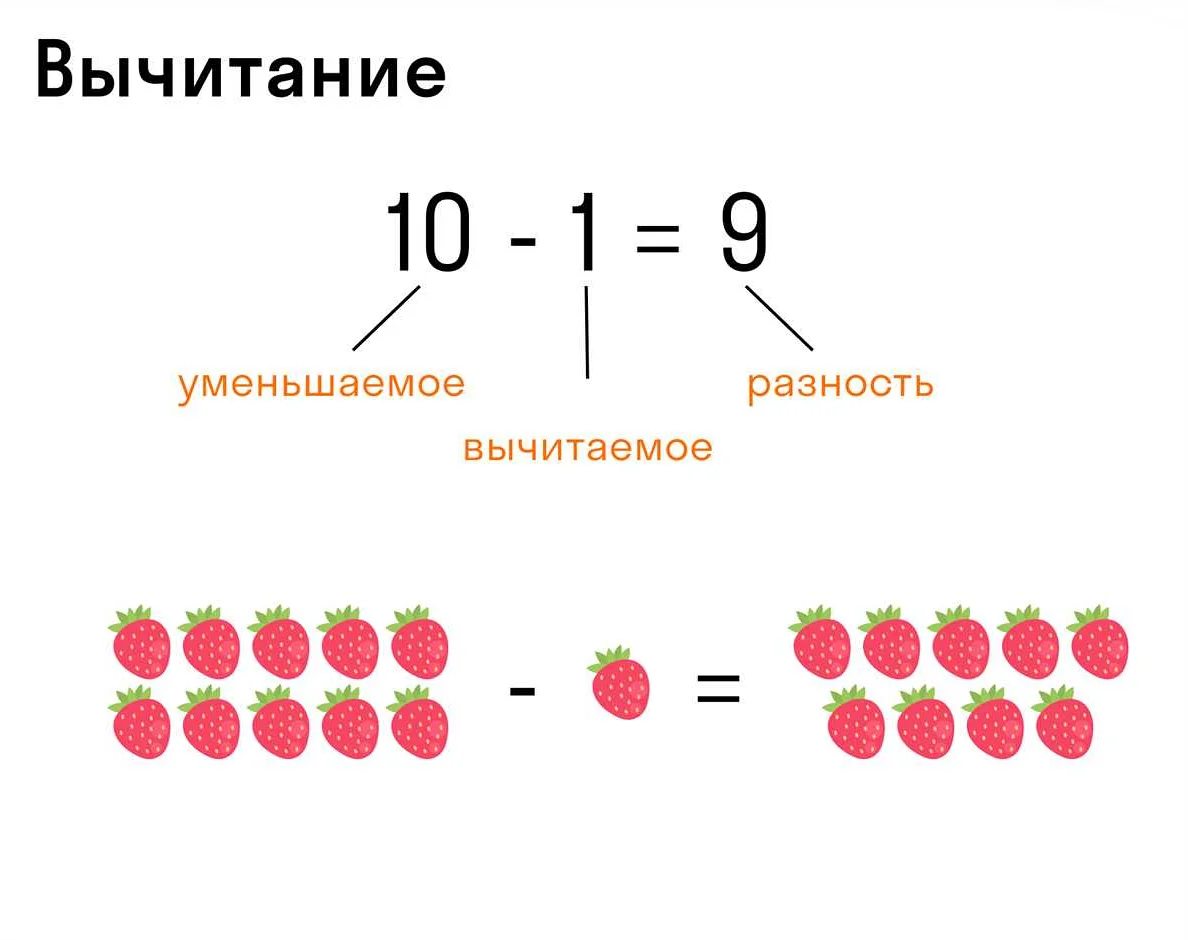
Вычитание — это операция, при которой одно число вычитается из другого числа. Например, при вычитании числа 3 из числа 5 получается число 2.

Умножение — это операция, при которой одно число увеличивается в несколько раз. Например, при умножении числа 2 на число 3 получается число 6.

Деление — это операция, при которой одно число делится на другое число. Например, при делении числа 6 на число 2 получается число 3.

Учение арифметике помогает развивать навыки работы с числами, а также решать различные задачи из реальной жизни.

Как сравнивать числа?

Наиболее распространенными знаками сравнения являются следующие:

• Знак «больше» (>), который указывает, что одно число больше другого.
• Знак «меньше» (
• Знак «больше или равно» (≥), который указывает, что одно число больше или равно другому.
• Знак «меньше или равно» (≤), который указывает, что одно число меньше или равно другому.

Для сравнения чисел также можно использовать словесные выражения, например:

• Число а больше числа б.
• Число а меньше числа б.
• Число а больше или равно числу б.
• Число а меньше или равно числу б.

Например, если сравниваем два числа: 5 и 3, то можно сказать, что 5 больше 3, а 3 меньше 5. Также можно сказать, что 5 больше или равно 3, а 3 меньше или равно 5.

Сравнение чисел в математике позволяет установить отношения между ними и использовать эти отношения при выполнении различных операций, например, при решении уравнений или построении графиков.

Как определить, на сколько одно число больше другого?

В математике, чтобы определить, насколько одно число больше другого, необходимо выполнить следующие действия:

1. Вычислите разницу между этими двумя числами.
2. Если разница положительная, то первое число больше второго на эту разницу.
3. Если разница отрицательная, то второе число больше первого на абсолютное значение этой разницы.

Например, если у нас есть числа 7 и 3:

• Вычисляем разницу: 7 — 3 = 4.
• Так как разница положительная, первое число (7) больше второго (3) на 4.

Аналогично, если у нас есть числа 5 и 8:

• Вычисляем разницу: 5 — 8 = -3.
• Так как разница отрицательная, второе число (8) больше первого (5) на абсолютное значение -3, то есть на 3.

Теперь вы знаете, как определить, на сколько одно число больше другого. Этот метод поможет вам легко сравнивать числа и определять их взаимное положение.

Понятие «на сколько больше» в контексте различных операций

В операции сложения, когда необходимо определить, на сколько больше одно число по сравнению с другим, мы вычисляем разницу между ними. Например, если мы сравниваем числа 7 и 3, то можно сказать, что число 7 на 4 больше числа 3.

В операции вычитания, понятие «на сколько больше» также используется для определения разницы между двумя числами. Если мы вычитаем число 3 из числа 7, то можно сказать, что число 7 на 4 больше числа 3.

В операции умножения, понятие «на сколько больше» применяется для определения разницы в результате умножения двух чисел. Например, если мы умножаем число 3 на 2, то можно сказать, что результат умножения на 2 больше исходного числа в 2 раза.

В операции деления, понятие «на сколько больше» применяется для определения разницы в результате деления двух чисел. Например, если мы делим число 6 на 3, то можно сказать, что результат деления на 3 больше исходного числа в 2 раза.

Таким образом, понятие «на сколько больше» в математике зависит от операции и позволяет сравнить числа и определить их разницу друг относительно друга.

Видео по теме:

Вопрос-ответ:

Как понять значение выражения «на сколько больше» в математике?

В математике, выражение «на сколько больше» используется для сравнения двух чисел и определения разницы между ними. Если число А больше числа В на сколько-то, это означает, что разница между А и В равна заданному числу.

Как можно применять понятие «на сколько больше» в реальной жизни?

Понятие «на сколько больше» может быть полезным во многих ситуациях. Например, при покупке товаров по акции, можно вычислить на сколько больше скидка составляет от обычной цены. Также, понятие «на сколько больше» может использоваться при анализе данных, чтобы определить, насколько одна величина превосходит другую.

Как вычислить разницу между двумя числами, используя понятие «на сколько больше»?

Чтобы вычислить разницу между двумя числами, используя понятие «на сколько больше», нужно вычесть меньшее число из большего. Результат будет показывать, на сколько больше первое число по сравнению со вторым.

Можно ли использовать понятие «на сколько больше» для отрицательных чисел?

Да, понятие «на сколько больше» можно применять и для отрицательных чисел. Если число А больше числа В на сколько-то, то это означает, что разница между ними отрицательна и равна абсолютному значению этой разницы.

Как поменять местами понятия «на сколько больше» и «на сколько меньше»?

Чтобы поменять местами понятия «на сколько больше» и «на сколько меньше», достаточно поменять местами сравниваемые числа. Если изначально число А было больше числа В на сколько-то, то после замены число В будет больше числа А на ту же самую величину.

Что означает выражение «на сколько больше»?

Выражение «на сколько больше» используется в математике для сравнения двух чисел и определения разницы между ними. Если сказать, что число А на сколько-то больше числа В, это означает, что разница между А и В равна указанному числу.

Как вычислить «на сколько больше» одно число по сравнению с другим?

Для вычисления «на сколько больше» одно число по сравнению с другим необходимо вычесть из большего числа меньшее число. Разница между этими числами и будет ответом на вопрос «на сколько больше». Например, если у нас есть число 8 и число 3, чтобы узнать «на сколько больше» число 8 по сравнению с числом 3, нужно вычесть 3 из 8, получив разницу 5.

Знак «больше» и его значение в математике

В математике знак «больше» имеет следующее значение:

• Сравнение чисел: Если число A больше числа B, то записывается как A > B. Например, если A = 5 и B = 3, то 5 > 3.
• Увеличение: Знак «больше» также используется для обозначения увеличения значения. Например, если число X увеличивается на 2, то записывается как X + 2 > X.
• Неравенство: Знак «больше» также используется для записи неравенства. Например, если A > B, то можно сказать, что A не равно B.

Знак «больше» является важным инструментом в математике, позволяющим сравнивать и анализировать числа и выражения. Он помогает определить отношения между числами и выполнять различные математические операции.

Примеры и задачи на определение «на сколько больше»

Пример 1:

ЧислоНа сколько большеОтвет

5	2	7
10	4	14
3	8	11

В этих примерах, числа 2, 4 и 8 являются «на сколько больше» для чисел 5, 10 и 3 соответственно.

Пример 2:

Компания А продала 100 единиц товара, а компания Б продала на 50 единиц товара больше. Найдите количество товара, проданного компанией Б.

Решение:

Чтобы найти количество товара, проданного компанией Б, нужно прибавить «на сколько больше» к количеству товара, проданного компанией А.

Количество товара, проданного компанией Б = Количество товара, проданного компанией А + «На сколько больше»

В данном случае:

Количество товара, проданного компанией А = 100

На сколько больше = 50

Количество товара, проданного компанией Б = 100 + 50 = 150

Таким образом, компания Б продала 150 единиц товара.

Эти примеры и задачи помогают разобраться в том, как определять «на сколько больше» и применять это понятие в математических расчетах и анализе данных.