Что значит по в математике

Узнайте, что означает понятие «по» в математике и как его использовать. Это важное понятие в алгебре и геометрии, которое помогает определить отношения и операции между элементами и множествами.

В математике термин «по» часто используется для обозначения отношений и операций между числами, объектами или переменными. Он может иметь разные значения в разных контекстах и играет важную роль в понимании и решении математических задач.

Один из наиболее распространенных смыслов термина «по» в математике — это указание на распределение или разделение чего-либо на равные части или группы. Например, «разделить массив по числу» означает разбить массив на равные группы с заданным числом элементов в каждой.

В другом контексте, «по» может означать выполнение операций или действий в отношении каждого элемента или члена некоторого множества. Например, «поэлементное сложение» означает сложение соответствующих элементов двух массивов или векторов.

Еще одним значением термина «по» в математике является указание на метод или алгоритм, используемый для решения задач. Например, «решить уравнение по методу Гаусса» означает использование метода Гаусса для нахождения корней уравнения.

Итак, термин «по» в математике имеет множество значений и применений. Он помогает определить отношения, операции и методы, используемые для анализа и решения математических задач. Понимание этих значений может быть полезным для более глубокого изучения математики и ее применения в реальном мире.

Что означает «по» в математике

В математике термин «по» используется для обозначения различных операций или действий, выполняемых с числами или выражениями. Он может иметь разные значения в разных контекстах, но в общем случае он указывает на то, что какое-то действие выполняется для каждого элемента или составляющей.

Например, если мы говорим «умножить число по таблице умножения», это означает, что мы умножаем данное число на каждое число от 1 до 10, как указано в таблице умножения. Такое использование «по» подразумевает последовательное применение операции к каждому элементу.

Другой пример использования «по» в математике — «сумма по ряду». Здесь «по» указывает, что мы складываем все элементы ряда по очереди. Такое использование «по» часто встречается в теории вероятностей и математическом анализе.

Также термин «по» может использоваться для обозначения диапазонов или интервалов. Например, «интеграл от a по b» означает, что мы интегрируем функцию на интервале от a до b. В этом случае «по» указывает на границы или пределы интегрирования.

В общем случае, значение «по» в математике может зависеть от контекста и специфики задачи. Важно понимать, что он обозначает последовательное применение операции к каждому элементу, использование диапазонов или интервалов, а также другие действия, выполняемые с числами или выражениями.

Определение понятия «по» в математике

В математике термин «по» используется для обозначения различных операций или действий, выполняемых с числами или другими объектами. Он может указывать на различные способы комбинирования, разделения или сравнения элементов.

Так, например, в выражении «3 по 5» термин «по» указывает на умножение чисел 3 и 5. Результатом данного выражения будет число 15.

Также термин «по» может означать разделение или распределение чего-либо. Например, «разделить 10 по 2» означает разделить число 10 на 2 равные части. Результатом будет число 5.

Кроме того, термин «по» может указывать на сравнение или классификацию объектов. Например, «сортировка по возрастанию» означает упорядочивание объектов в порядке возрастания их значений.

Термин «по» широко используется в различных математических операциях и алгоритмах, и его значение зависит от контекста и задачи, которую необходимо решить.

Значение «по» в выражениях и уравнениях

В математике, слово «по» часто используется для обозначения некоторых отношений и операций в выражениях и уравнениях. Оно может иметь различные значения в разных контекстах, но в целом его использование связано с указанием способа выполнения действия или операции.

Например, в выражении «2 по 3» слово «по» указывает на операцию умножения. Это означает, что число 2 умножается на число 3, что дает результат 6. Таким образом, выражение «2 по 3» можно перевести как «2 умножить на 3».

Еще одним примером использования слова «по» в математике является выражение «деление по модулю». В этом случае, слово «по» указывает на операцию деления числа на другое число с остатком. Например, если мы рассмотрим выражение «10 по 3», оно означает, что число 10 делится на число 3 с остатком 1.

Кроме того, слово «по» может использоваться для обозначения диапазона значений или интервала. Например, выражение «x по y» может обозначать, что переменная x принимает значения в диапазоне от некоторого значения x1 до другого значения x2, где x1 и x2 заданы в терминах переменной y.

В заключение, использование слова «по» в математике зависит от контекста и может иметь различные значения. Оно может указывать на операции, диапазоны значений или другие отношения между переменными и значениями.

Понятие «по» в контексте функций

В математике понятие «по» может применяться и в контексте функций. Когда мы говорим о функции, мы обычно имеем в виду отображение, которое каждому элементу из одного множества ставит в соответствие элемент из другого множества.

Используя понятие «по», мы можем указать, как именно происходит это отображение. Например, если у нас есть функция f, которая отображает элементы из множества X в элементы из множества Y, мы можем сказать, что f отображает элементы «по формуле» или «по правилу». Это означает, что для каждого элемента x из X существует определенное правило, по которому мы получаем соответствующий элемент y из Y.

Давайте рассмотрим пример. Пусть у нас есть функция f, которая отображает целые числа в их квадраты. Мы можем записать это как f(x) = x^2. Здесь «по» означает, что для каждого целого числа x существует правило, по которому мы получаем его квадрат.

Таким образом, понятие «по» в контексте функций используется для указания способа отображения элементов одного множества в элементы другого множества.

XY

1	1
2	4
3	9
4	16

Примеры использования «по» в математике

В математике термин «по» может использоваться в различных контекстах и иметь разные значения. Вот несколько примеров:

1. Умножение числа «по» другому числу:

Если у нас есть число, которое нужно умножить на другое число, то мы можем использовать «по» для обозначения этой операции. Например, 5 по 3 равно 15. Это означает, что мы берем число 5 и умножаем его на 3.

2. Деление числа «по» другому числу:

Точно так же, как и с умножением, мы можем использовать «по» для обозначения деления. Например, 15 по 3 равно 5. Это означает, что мы берем число 15 и делим его на 3.

3. Интервал значений «по» переменной:

В математике «по» может использоваться для обозначения интервала значений переменной. Например, если у нас есть функция f(x) = x^2, то мы можем сказать, что x принадлежит интервалу от -∞ до +∞. Это можно записать как x «по» реальным числам.

4. Шаг «по» переменной:

Когда мы работаем с последовательностью чисел или графиком функции, мы можем использовать «по» для обозначения шага, с которым меняется переменная. Например, если у нас есть последовательность чисел 1, 3, 5, 7, 9, …, то мы можем сказать, что она формируется с шагом 2 «по» натуральным числам.

Это лишь некоторые примеры использования «по» в математике. В каждом конкретном случае контекст и значение этого термина могут отличаться. Важно учитывать эти различия и понимать, что «по» может иметь разные значения в разных математических выражениях.

Роль «по» в математических операциях

В математике термин «по» используется для обозначения действия, выполняемого с каждым элементом некоторого множества. В зависимости от контекста, «по» может иметь различные значения и использоваться в различных операциях.

Например, в операции умножения «по» означает, что каждый элемент одного множества умножается на каждый элемент другого множества. Таким образом, результатом операции умножения «по» будет новое множество, содержащее все возможные комбинации умножений элементов первого и второго множеств.

Аналогично, в операции сложения «по» означает, что каждый элемент одного множества складывается с каждым элементом другого множества. Таким образом, результатом операции сложения «по» будет новое множество, содержащее все возможные комбинации сложений элементов первого и второго множеств.

Кроме умножения и сложения, «по» может использоваться и в других операциях, таких как деление, вычитание и возведение в степень. В каждом случае «по» указывает на то, что операция выполняется с каждым элементом множества.

Например, в операции деления «по» каждый элемент делимого множества делится на каждый элемент делителя, а результатом будет новое множество, содержащее все возможные комбинации делений.

Таким образом, «по» в математических операциях указывает на выполнение операции с каждым элементом множества и позволяет получить новое множество, содержащее все возможные комбинации операций.

Зависимость от «по» в графиках и геометрии

Термин «по» в математике используется для указания зависимости одной величины от другой. В графиках и геометрии «по» часто используется для обозначения зависимости переменных и отображения этой зависимости на графике или в пространстве.

Например, в графике функции «y = f(x)» переменная «x» обозначает независимую величину, а переменная «y» зависимую величину. Таким образом, можно сказать, что значение «y» определяется «по» значению «x».

В геометрии «по» используется для обозначения зависимости размеров или положения фигур друг относительно друга. Например, можно сказать, что длина отрезка «AB» определяется «по» координатам точек «A» и «B».

Также, «по» может использоваться для обозначения действия или операции, которая выполняется в соответствии с определенным правилом или алгоритмом. Например, можно сказать, что прямая «l» проведена «по» двум точкам «A» и «B», что означает, что прямая проходит через эти две точки.

Видео по теме:

Вопрос-ответ:

Что означает «по» в математике?

В математике слово «по» может иметь различные значения. Оно может обозначать операцию умножения, деление или вычитания, а также указывать на то, что какое-то действие выполняется для каждого элемента множества. В зависимости от контекста, значение слова «по» может меняться.

Какое значение имеет «по» в операции умножения?

В операции умножения слово «по» используется для обозначения операции умножения двух чисел или выражений. Например, 2 по 3 означает, что число 2 нужно умножить на 3, что даст результат 6.

Как «по» используется в операции деления?

В операции деления слово «по» обозначает, что одно число делится на другое. Например, 10 по 2 означает, что число 10 делится на 2, что даст результат 5.

Как «по» используется для указания на действие, выполняемое для каждого элемента множества?

Когда слово «по» используется для указания на действие, выполняемое для каждого элемента множества, оно обычно ставится перед формулой или выражением, которые описывают это действие. Например, если есть множество чисел {1, 2, 3}, то сумма каждого числа из этого множества будет выглядеть как «сумма по множеству {1, 2, 3}». Такое использование слова «по» позволяет указать, что действие выполняется для каждого элемента множества.

Применение «по» в математической логике

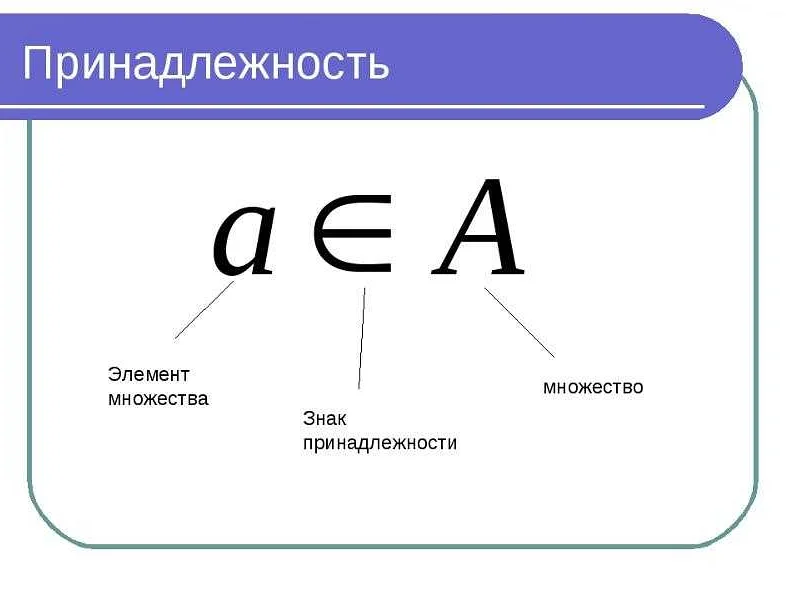
Например, если у нас есть переменная x, которая может принимать значения от 1 до 10, мы можем записать это как «x принадлежит диапазону от 1 по 10» или «x ∈ [1, 10]». Это означает, что x может быть равным 1, 2, 3 и так далее, до 10 включительно.

Также «по» может использоваться для описания шага или инкремента при итерации или переборе значений. Например, если мы хотим перебрать все четные числа от 1 до 10, мы можем записать это как «i перебирает значения от 2 по 10 с шагом 2» или «i ∈ [2, 10] с шагом 2». Это означает, что i будет принимать значения 2, 4, 6, 8 и 10.

Таким образом, использование «по» в математической логике позволяет удобно и компактно указывать диапазоны значений или переменных, а также задавать шаг или инкремент при итерации или переборе.

Важность понимания значения «по» в математике

Когда мы говорим «x по y», это означает, что переменная x зависит от переменной y или меняется в соответствии с изменениями в переменной y. Например, если мы говорим «увеличение x на 2 по увеличению y на 1», это означает, что каждый раз, когда значение y увеличивается на 1, значение x увеличивается на 2.

Использование «по» также позволяет нам определить функциональные отношения между переменными. Например, если у нас есть функция f(x) = 2x, мы можем сказать, что f(x) растет «по x». Это означает, что при увеличении значения x, значение f(x) также увеличивается.

Понимание значения «по» в математике позволяет нам более точно формулировать и решать математические задачи. Оно помогает нам определить взаимосвязь между переменными и понять, как одна переменная влияет на другую. Без понимания значения «по», мы можем неправильно интерпретировать математические уравнения и получить неверные результаты.

ПримерЗначение «по»

Уравнение: y = 2x	y растет по x
Уравнение: A = πr^2	Площадь круга A зависит от радиуса r
Уравнение: V = lwh	Объем прямоугольного параллелепипеда V зависит от длины l, ширины w и высоты h

Выводящий абзац.