Формулы, которые необходимо знать для успешной сдачи ЕГЭ по математике

Узнайте, какие формулы необходимо знать на экзамене ЕГЭ по математике. От простых до сложных, этот список поможет вам лучше подготовиться к экзамену и облегчить свой процесс изучения.

ЕГЭ по математике является одним из самых сложных испытаний для многих школьников. В процессе подготовки к экзамену необходимо не только повторить основные темы, но и запомнить множество формул. Однако, общая информация о том, какие формулы следует знать, часто оказывается недостаточной для эффективной подготовки.

В этой статье мы расскажем о наиболее важных и необходимых формулах, которые следует знать для успешной сдачи ЕГЭ по математике. Наш список содержит все основные формулы, которые необходимы для понимания математических концепций на экзамене, а также примеры, как они могут быть применены в практических задачах ЕГЭ.

Необходимо отметить, что знание формул — это только часть предмета. Для полноценной подготовки необходимо также понимать, как применять формулы в жизненных и математических ситуациях, что также является частью ЕГЭ по математике. Тем не менее, без правильной базы знаний, включающей формулы, трудно будет успешно сдать экзамен.

ЕГЭ по математике: формулы, которые нужно знать

ЕГЭ по математике – это один из самых важных экзаменов в жизни студента. Для того чтобы успешно сдать экзамен, необходимо хорошо освоить все формулы, которые могут быть заданы на тесте.

Студенты должны помнить формулы тригонометрии, например, формулу синусов или формулу косинусов. Кроме того, необходимо уметь решать квадратные уравнения и знать, как использовать формулу дискриминанта.

• Формула синусов: sin α / a = sin β / b = sin γ / c
• Формула косинусов: a² = b² + c² — 2bc cos α
• Формула дискриминанта: D = b² — 4ac

Кроме того, студенты должны знать формулу геометрической прогрессии (a₁ / 1 — q), формулу поиска площади треугольника (S = 1/2 × a × h) и формулу для расчета объема цилиндра (V = π × r² × h)

1. Формула геометрической прогрессии: a₁ / 1 — q
2. Формула поиска площади треугольника: S = 1/2 × a × h
3. Формула для расчета объема цилиндра: V = π × r² × h

Это лишь некоторые формулы, которые могут быть заданы на экзамене ЕГЭ по математике. Помните, что хорошо подготовленный студент не боится трудностей и успешно справится с экзаменом, если знает все необходимые формулы и умеет их применять.

Правила действий с числами

В математике существуют определенные правила действий с числами, которые необходимо знать перед сдачей ЕГЭ по данному предмету. Они позволяют выполнять различные операции с цифрами и получать правильные ответы.

Одно из таких правил — правило знаков. Его суть заключается в том, что при сложении или вычитании чисел разного знака нужно вычитать модули чисел и прибавлять к результату знак большего по модулю числа:

• если числа имеют одинаковый знак, то складываем их модули и добавляем знак
• если числа имеют разные знаки, то вычитаем из большего по модулю числа модуль меньшего и прибавляем знак большего по модулю числа

Другое важное правило — правило приоритетов операций. Оно гласит, что при выполнении нескольких операций нужно сначала выполнять умножение и деление, а затем сложение и вычитание.

Кроме того, стоит знать правила действий с дробями, такие как умножение и деление дробей, а также перевод дробей из обычной в десятичную форму и обратно.

Правила действий с дробямиДействиеФормула

Умножение	a/b × c/d = (a × c)/(b × d)
Деление	a/b ÷ c/d = (a × d)/(b × c)
Перевод в десятичную форму	Деление числителя на знаменатель
Перевод из десятичной формы	Число записывается в виде дроби, где знаменатель является 10 в степени количества цифр после запятой, а числитель сокращается

Простейшие алгебраические формулы

Алгебра — это раздел математики, который изучает структуру и свойства математических объектов, таких как числа, переменные, операции над ними и т.д. Простейшие алгебраические формулы — это формулы, которые можно выразить через операции сложения, вычитания, умножения и деления.

Некоторые из этих формул:

• Формула сложения: a + b = b + a
• Формула вычитания: a — b = -(b — a) = -(b — a)
• Формула умножения: a ∙ b = b ∙ a
• Формула деления: a / b = a ∙ (1 / b)

Эти формулы будут полезны при решении различных задач в математике и еще многих других областях науки.

Тригонометрические формулы

Тригонометрические формулы очень важны при решении задач, связанных с изучением угловых функций. Необходимо знать основные формулы, которые помогут решить большинство задач.

Одной из наиболее известных тригонометрических формул является формула синусов: a/sin A = b/sin B = c/sin C. С ее помощью можно найти отсутствующий угол или сторону в треугольнике.

Еще одной важной формулой является формула косинусов: a^2 = b^2 + c^2 — 2bc cos A. Она также может быть использована для нахождения отсутствующей стороны или угла в треугольнике.

К тригонометрическим формулам относится и формула тангенса: tan A = sin A/cos A. Она помогает вычислять тангенс угла, если известны значение синуса и косинуса.

• Формула синусов: a/sin A = b/sin B = c/sin C
• Формула косинусов: a^2 = b^2 + c^2 — 2bc cos A
• Формула тангенса: tan A = sin A/cos A

Кроме того, существует формула котангенса: cot A = 1/tan A = cos A/sin A. Она позволяет вычислять котангенс угла, если известны значение синуса и косинуса.

Также существует формула косинусов для нахождения площади треугольника: S = 1/2 ab sin C. Она используется для вычисления площади треугольника, если известны две стороны и угол между ними.

Название формулыФормула

Формула синусов	a/sin A = b/sin B = c/sin C
Формула косинусов	a^2 = b^2 + c^2 — 2bc cos A
Формула тангенса	tan A = sin A/cos A
Формула котангенса	cot A = 1/tan A = cos A/sin A
Формула косинусов для площади треугольника	S = 1/2 ab sin C

Геометрические формулы

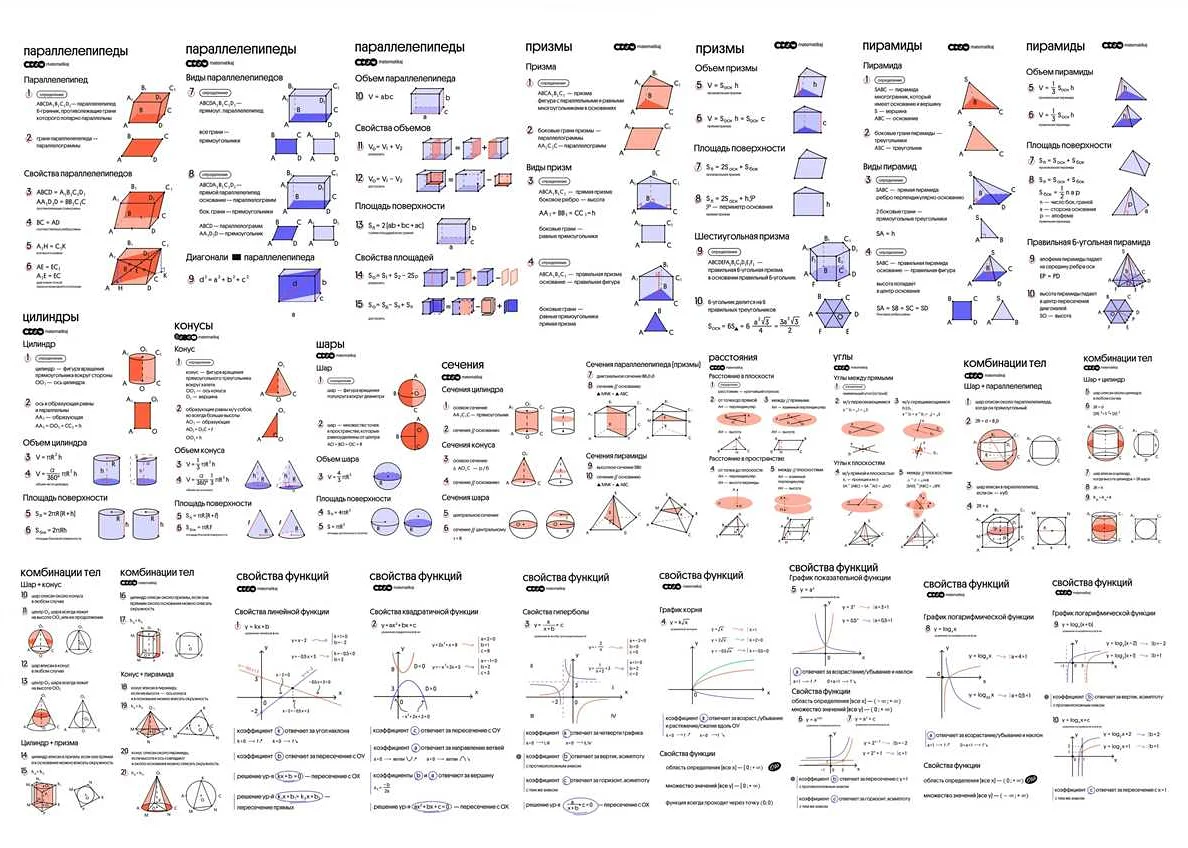
Площадь прямоугольника: S = a * b (где a и b — длины сторон)

Периметр прямоугольника: P = 2a + 2b

Площадь круга: S = πr² (где π≈3,14, r — радиус круга)

Длина окружности: L = 2πr

Площадь треугольника: S = 0,5 * a * h (где a — основание треугольника, h — высота проведенная к основанию)

Теорема Пифагора: a² + b² = c² (где a, b — катеты прямоугольного треугольника, c — гипотенуза)

Формула греческих огней: S = a * p / 2 (где a, b, c — стороны треугольника, p — полупериметр)

Формула синусов: a/sinA = b/sinB = c/sinC (где a, b, c — стороны треугольника, A, B, C — соответствующие им углы)

Формула косинусов: a² = b² + c² — 2bc*cosA (где a, b, c — стороны треугольника, A — угол между сторонами b и c)

Формула высоты: h = 2S/a (где S — площадь треугольника, а — основание к которому проведена высота)

Формулы для нахождения длин, площадей и объемов

При решении задач на ГИА и ЕГЭ по математике часто требуется находить длины сторон, площади и объемы различных геометрических фигур. Для этого необходимо знать соответствующие формулы.

Формулы для нахождения длин различных линий:

• Длина окружности: L = 2πr или L = πd, где r — радиус окружности, d — диаметр окружности, π = 3,14.
• Длина отрезка: AB = √(x2 — x1)2 + (y2 — y1)2, где A(x1, y1) и B(x2, y2) — координаты точек A и B на координатной плоскости.
• Длина дуги: L = rα, где r — радиус окружности, α — угол, соответствующий дуге в радианах.

Формулы для нахождения площадей различных фигур:

• Площадь круга: S = πr2, где r — радиус окружности, π = 3,14.
• Площадь треугольника: S = 1/2 * a * h, где а — длина основания треугольника, h — высота треугольника, опущенная на основание.
• Площадь прямоугольника: S = a * b, где a и b — длины сторон прямоугольника.

Формулы для нахождения объемов и поверхностей различных тел:

• Объем куба: V = a3, где a — длина ребра куба.
• Объем цилиндра: V = πr2h, где r — радиус основания цилиндра, h — высота цилиндра, π = 3,14.
• Площадь поверхности сферы: S = 4πr2, где r — радиус сферы, π = 3,14.

Знание данных формул позволит значительно облегчить решение задач на ГИА и ЕГЭ по математике и увеличит шансы на успешную сдачу экзаменов.

Формулы для расчета процентов

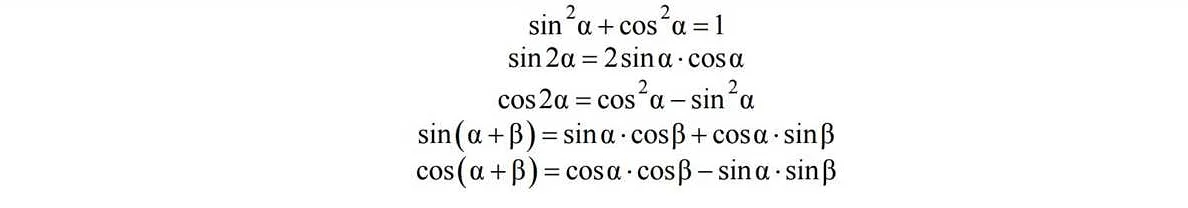
1. Процент от числа

Для расчета процента от числа, нужно умножить число на процент и разделить на 100:

Процент от числа = (Число x Процент) / 100

2. Изменение в процентах

Чтобы найти изменение числа в процентах, нужно найти разницу между конечным числом и начальным числом, разделить это на начальное число и умножить на 100:

Изменение в процентах = ((Конечное число – Начальное число) / Начальное число) x 100

3. Процентное изменение

Процентное изменение вычисляется как разница процентного отношения конечного числа к начальному числу к 100%:

Процентное изменение = ((Конечное число / Начальное число) – 1) x 100

4. Увеличение числа на процент

Для расчета увеличения числа на определенный процент, нужно добавить к числу процентную долю от него:

Увеличение числа на процент = Число x ((100 + Процент) / 100)

5. Уменьшение числа на процент

Для расчета уменьшения числа на определенный процент, нужно вычесть из числа процентную долю от него:

Уменьшение числа на процент = Число x ((100 — Процент) / 100)

6. Процент от суммы

Для расчета процента от суммы, нужно умножить сумму на процент и разделить на 100:

Процент от суммы = (Сумма x Процент) / 100

Формулы для работы с функциями

Формула линейной функции:

Если дана линейная функция вида y = kx + b, где k — коэффициент наклона, b — свободный член, то:

y2 — y1 = k(x2 — x1)

Формула квадратичной функции:

Если дана квадратичная функция вида y = ax2 + bx + c, то:

x = (-b ± √(b2 — 4ac)) / 2a

Формула обратной функции:

Если дана функция f(x) и ее обратная функция f-1(x), то:

f-1(f(x)) = x

Формула нахождения точки экстремума функции:

Если дана функция y = f(x), то:

x = -b / 2a

Формула нахождения производной:

Если дана функция y = f(x), то:

f'(x) = limh→0 (f(x + h) — f(x)) / h

Формула нахождения интеграла:

Если дана функция y = f(x), то:

∫f(x)dx = F(x) + C

Формула Эйлера:

Если дана комплексная функция вида eix = cos x + i sin x, то:

eiπ + 1 = 0

• Формула линейной функции позволяет находить угол наклона графика в заданных точках.
• Формула квадратичной функции используется для нахождения корней уравнения, которое образовано приравниванием квадратичной функции к нулю.
• Формула обратной функции помогает найти значение аргумента, если известно значение функции.
• Формула нахождения точки экстремума функции используется для определения максимума или минимума функции.
• Формула нахождения производной применяется для нахождения скорости изменения функции в заданной точке.
• Формула нахождения интеграла используется для нахождения площади под графиком функции.
• Формула Эйлера связывает три важных математических константы: e, i, π.

Формулы для нахождения корней квадратного уравнения

Квадратное уравнение имеет вид ax2 + bx + c = 0, где a, b и c — произвольные числа. Корнями квадратного уравнения являются значения переменной x, при которых уравнение выполняется.

Формула для нахождения корней квадратного уравнения: x1,2 = (-b ± √D) / 2a, где D — дискриминант, вычисляемый по формуле D = b2 — 4ac. Если D > 0, то уравнение имеет два различных вещественных корня, если D = 0, то уравнение имеет один корень, а если D < 0, то уравнение не имеет вещественных корней.

Также существуют другие формулы для нахождения корней квадратного уравнения, например, метод завершения квадрата или метод Виета. Однако формула, записанная выше, является наиболее универсальной и часто используемой в школьной программе.

Необходимость знания формулы для нахождения корней квадратного уравнения связана с решением различных задач математического анализа, физики и техники. Кроме того, эта формула может быть полезна при решении некоторых практических задач, связанных с расчетами и измерениями.

Формулы для работы с логарифмами

Логарифм — это математическая функция, которая используется для преобразования числа из обычного числового формата в экспоненциальный вид. Функция логарифма выполняет обратную операцию по отношению к возведению чисел в степень. Учитывая значительное значение логарифмов в математике, необходимо знать основные формулы для работы с логарифмами на ЕГЭ по математике.

• Формула логарифма в базе а: logab = c, где a является базой логарифма, b– число, которое возводится в степень, а c – логарифм от b в базе а.
• Формула для логарифма суммы: loga(b + c) = logab + logac. Она позволяет вычислять логарифм суммы двух чисел, которые могут быть выражены в виде логарифмов.
• Формула для логарифма произведения: loga(bc) = logab + logac. Она позволяет вычислять логарифм произведения двух чисел, которые могут быть выражены в виде логарифмов.
• Формула для логарифма частного: loga(b/c) = logab — logac. Она позволяет вычислять логарифм частного двух чисел, которые могут быть выражены в виде логарифмов.

Хорошее знание теории логарифмов и умение работать с основными формулами поможет подготовиться к ЕГЭ по математике.

Видео по теме:

Вопрос-ответ:

Какие формулы необходимо знать для успешной сдачи ЕГЭ по математике?

Для успешной сдачи ЕГЭ по математике необходимо знать множество формул, в том числе формулы геометрических фигур, формулы тригонометрии, формулы для работы с функциями и др. Конкретный перечень формул можно найти в официальном учебном пособии «Математика. ЕГЭ. Задания разных уровней сложности».

Что такое теорема Пифагора и как ее использовать на ЕГЭ?

Теорема Пифагора устанавливает соотношение между длинами сторон прямоугольного треугольника: квадрат гипотенузы равен сумме квадратов катетов. Эта теорема используется для решения задач на геометрию, связанных с прямоугольными треугольниками. Например, можно находить длину стороны треугольника, если известны длины двух других сторон. Также теорема Пифагора может быть использована для доказательства тождественных тригонометрических выражений.

Как пользоваться формулами тригонометрии на ЕГЭ?

Формулы тригонометрии могут быть использованы для решения задач на геометрию, связанных с треугольниками и окружностями. Например, можно найти значение тангенса, когда известны значения синуса и косинуса, а также определить углы между сторонами треугольника по известным длинам сторон. Конкретный перечень формул тригонометрии можно найти в официальном учебном пособии «Математика. ЕГЭ. Задания разных уровней сложности».

Зачем нужна формула Герона?

Формула Герона используется для нахождения площади треугольника по длинам его сторон. Эта формула может быть использована в задачах на геометрию, связанных с треугольниками. Например, можно находить площадь треугольника, если известны длины всех его сторон.

Какие формулы используются для работы с функциями?

Для работы с функциями на ЕГЭ необходимо знать формулы для вычисления значения функции, ее производной и интеграла. Например, для вычисления значения функции в определенной точке можно использовать формулу f(x) = y, где x — аргумент функции, y — значение функции в точке x. Для вычисления производной функции необходимо знать формулу f'(x) = lim(h -> 0) (f(x + h) — f(x)) / h, где h — бесконечно малая величина. Для вычисления интеграла функции необходимо знать формулу ∫a^b f(x) dx = F(b) — F(a), где F(x) — первообразная функции f(x).

Какие формулы используются для работы с геометрическими фигурами?

Для работы с геометрическими фигурами на ЕГЭ необходимо знать множество формул для нахождения их характеристик, таких как площадь, периметр и длина дуги. Например, для нахождения площади круга необходимо знать формулу S = π r^2, где r — радиус круга, а π — число пи. Для нахождения периметра треугольника необходимо знать формулу P = a + b + c, где a, b и c — длины его сторон. Конкретный перечень формул можно найти в официальном учебном пособии «Математика. ЕГЭ. Задания разных уровней сложности».

Какова формула длины дуги окружности?

Формула длины дуги окружности представляет собой произведение длины окружности на долю угла с центром в центре окружности, соответствующую данной дуге. Формула имеет вид L = r * α, где L — длина дуги, r — радиус окружности, α — угол в радианах. Для перевода угла из градусов в радианы необходимо умножить его на π/180.

Формулы для работы со статистикой

В математике статистика относится к области, которая изучает различные виды данных и их анализ. Ниже приведены формулы, которые следует знать при работе со статистическими данными.

• Среднее арифметическое: среднее арифметическое — это сумма всех значений, деленная на количество значений.
• Медиана: медиана — это число, которое делит набор данных пополам. То есть половина данных меньше медианы, а другая половина больше.
• Стандартное отклонение: стандартное отклонение — это мера изменчивости или разброса данных вокруг среднего значения.
• Коэффициент корреляции: коэффициент корреляции — это мера связи между двумя наборами данных.
• Дисперсия: дисперсия — это мера распределения данных относительно их среднего значения.

Важно помнить, что эти формулы используются в зависимости от целей и задач, которые требуется решить при анализе статистических данных. Поэтому необходимо уметь выбирать правильную формулу для работы с набором данных и правильно интерпретировать полученные результаты.

Некоторые дополнительные формулы

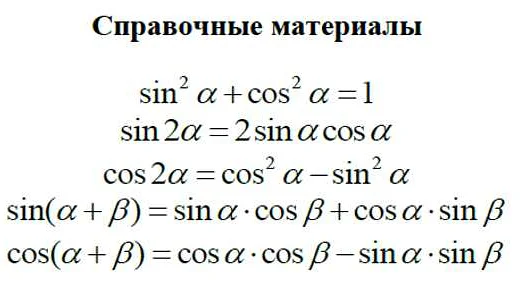
Кроме стандартных формул, которые используются на экзамене по математике, есть еще несколько дополнительных, которые могут быть полезными при решении задач.

Формула суммы членов арифметической прогрессии:

Если a1 — первый член арифметической прогрессии, d — ее разность, а n — количество членов в прогрессии, то сумма членов прогрессии будет равна:

S = (a1 + an) / 2 * n

Формула суммы членов геометрической прогрессии:

Если a1 — первый член геометрической прогрессии, q — ее знаменатель, а n — количество членов в прогрессии, то сумма членов прогрессии будет равна:

S = a1 * (1 — q^n) / (1-q)

Формула произведения суммы и разности двух квадратов:

a^2 — b^2 = (a + b) * (a — b)

Эту формулу можно использовать для упрощения выражений с двумя квадратами, например:

x^2 — 4 = (x — 2) * (x + 2)

Теорема Пифагора:

Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов:

c^2 = a^2 + b^2

Теорема косинусов:

Теорема косинусов позволяет вычислить длину одного из катетов прямоугольного треугольника, если известны длины другого катета и гипотенузы, а также угол между этими сторонами:

a^2 = b^2 + c^2 — 2bc*cos(A)

где А — угол между сторонами b и c.