Формулы которые нужны для егэ по математике
Содержимое
- 1 Формулы которые нужны для егэ по математике
- 1.1 Важность математических формул для ЕГЭ
- 1.2 Раздел 1: Алгебра
- 1.3 Формулы для работы с многочленами
- 1.4 Раздел 2: Геометрия
- 1.5 Формулы для вычисления площади и объема
- 1.6 Раздел 3: Тригонометрия
- 1.7 Формулы для вычисления синуса, косинуса и тангенса
- 1.8 Раздел 4: Вероятность и статистика
- 1.9 Видео по теме:
- 1.10 Вопрос-ответ:
- 1.10.0.1 Какие формулы являются самыми важными для сдачи ЕГЭ по математике?
- 1.10.0.2 Как применить формулу Герона для нахождения площади треугольника по длинам его сторон?
- 1.10.0.3 Какая формула используется для нахождения площади круга?
- 1.10.0.4 Как применить формулу синусов для нахождения длин сторон треугольника и его углов?
- 1.11 Формулы для вычисления вероятности событий
- 1.12 Раздел 5: Логарифмы
Узнайте о важных математических формулах, которые необходимо знать для успешной сдачи ЕГЭ по математике. В данной статье вы найдете основные формулы по алгебре, геометрии и тригонометрии, которые помогут вам решать задачи на экзамене.
Математика — один из самых важных предметов на ЕГЭ, так как она составляет значительную часть экзамена. Одним из ключевых навыков, которые должен освоить абитуриент, является умение работать с формулами. Необходимо знать, как применять формулы, чтобы решать задачи из разных областей математики.
Самые важные формулы для ЕГЭ включают в себя теоремы и правила, которые помогут решить большинство задач. Например, формулы тригонометрии, геометрии, алгебры и арифметики используются для решения задач, связанных с треугольниками, окружностями, функциями, пропорциями и т.д.
Одной из самых известных формул, которую следует запомнить, является формула Пифагора: a² + b² = c², где a и b — длины катетов, а c — длина гипотенузы в прямоугольном треугольнике. Данная формула используется для решения задач, связанных с прямоугольными треугольниками, например, для нахождения длины стороны или высоты треугольника.
Кроме того, формулы могут быть использованы для решения задач, связанных с функциями, производными, интегралами и т.д. Например, формула для расчета площади круга S = πr², где r — радиус, может быть использована для решения задач, связанных с геометрией и аналитической геометрией.
Следует отметить, что знание формул является только одним из аспектов подготовки к ЕГЭ по математике. Важно также уметь применять их в различных ситуациях и анализировать задачи, чтобы выбрать наиболее подходящую формулу для решения. Поэтому регулярное практикование решения задач с использованием формул является необходимым условием для успешной сдачи ЕГЭ по математике.
Важность математических формул для ЕГЭ
Формулы помогают ученикам вычислять и находить решения задач, определять зависимости между величинами, анализировать данные, проводить вычисления и доказательства. Они позволяют учиться сознательному применению математических методов и операций.
Знание формул позволяет существенно экономить время при решении задач на ЕГЭ. Умение распознавать и применять необходимую формулу позволяет быстро перейти от условия задачи к построению алгоритма решения. Таким образом, ученик может сосредоточиться на самом решении, а не тратить время на поиск и восстановление формул.
Кроме того, формулы являются инструментом для проверки правильности решений. Они позволяют ученику контролировать и сверять свои вычисления, отслеживать ошибки и искать пути их исправления.
Важно отметить, что на ЕГЭ часто встречаются задачи, в которых нужно применять несколько формул одновременно. Поэтому знание и понимание формул позволяет более эффективно решать задачи и повышает вероятность успешного выполнения экзамена.
В заключение, математические формулы являются неотъемлемой частью подготовки к ЕГЭ по математике. Они помогают ученикам развивать логическое мышление, аналитические навыки и критическое мышление. Знание и умение применять формулы позволяет успешно решать задачи и получать высокие баллы на экзамене.
Раздел 1: Алгебра
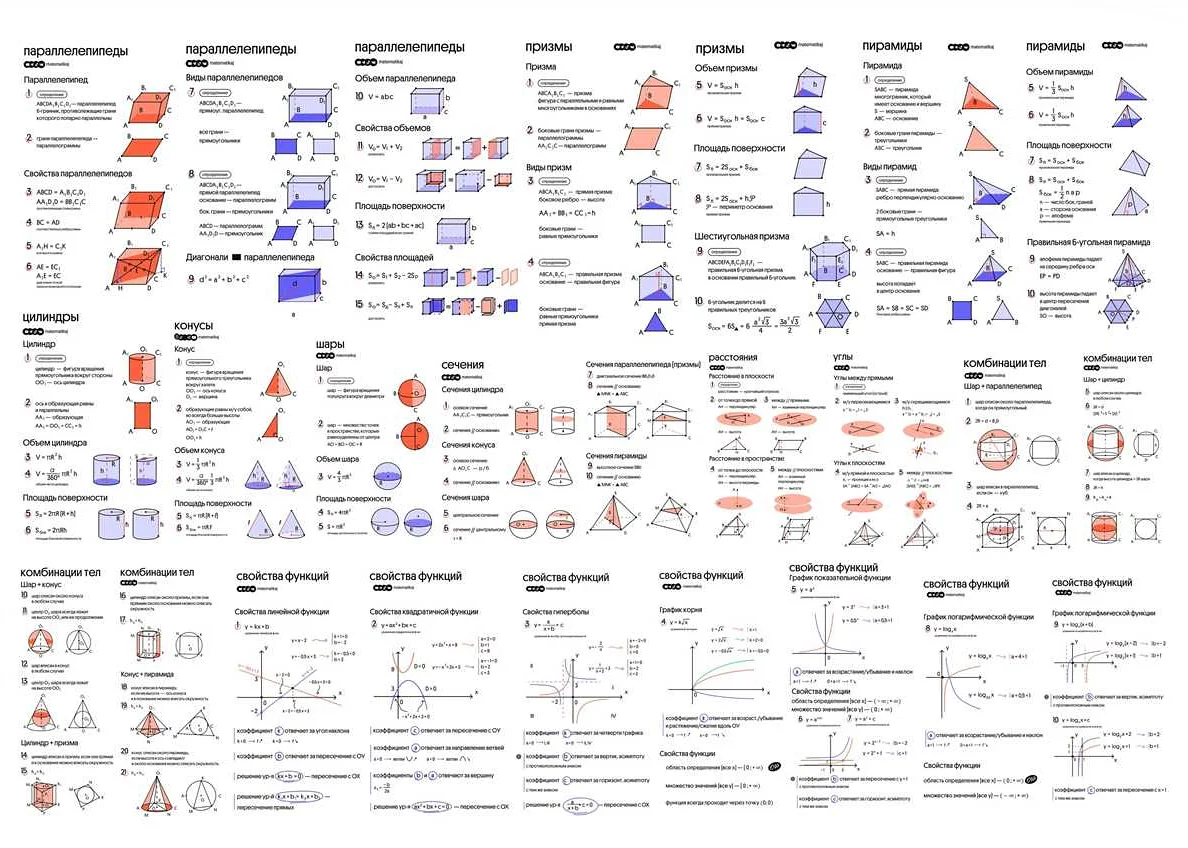
В данном разделе мы рассмотрим самые важные алгебраические формулы, которые пригодятся на экзамене.
ФормулаОписание
| (a + b)^2 = a^2 + 2ab + b^2 | Квадрат суммы двух чисел равен сумме квадратов этих чисел и удвоенному произведению |
| (a — b)^2 = a^2 — 2ab + b^2 | Квадрат разности двух чисел равен разности квадратов этих чисел и удвоенному произведению |
| a^2 — b^2 = (a + b)(a — b) | Разность квадратов двух чисел равна произведению суммы и разности этих чисел |
| a^3 + b^3 = (a + b)(a^2 — ab + b^2) | Сумма кубов двух чисел равна произведению суммы и разности кубов этих чисел |
| a^3 — b^3 = (a — b)(a^2 + ab + b^2) | Разность кубов двух чисел равна произведению разности и суммы кубов этих чисел |
| a^n — b^n = (a — b)(a^(n-1) + a^(n-2)b + … + ab^(n-2) + b^(n-1)) | Разность степеней двух чисел равна произведению разности и суммы степеней этих чисел |
Кроме того, в алгебре важно знать и уметь применять основные свойства арифметических операций, такие как коммутативность, ассоциативность и дистрибутивность. Эти свойства позволяют упростить выражения и выполнить алгебраические преобразования.
Важно не только знать формулы, но и уметь применять их в различных задачах. Для этого необходимо понимать суть формулы и уметь адаптировать ее под конкретную задачу. Поэтому регулярная тренировка и решение разнообразных задач помогут улучшить навыки алгебраических вычислений и успешно сдать ЕГЭ по математике.
Формулы для работы с многочленами
Формула сложения многочленов: чтобы сложить два многочлена, нужно сложить соответствующие члены многочленов. Например, (3x^2 + 2x + 1) + (2x^2 + x + 3) = 5x^2 + 3x + 4.
Формула вычитания многочленов: чтобы вычесть один многочлен из другого, нужно вычесть соответствующие члены многочленов. Например, (3x^2 + 2x + 1) — (2x^2 + x + 3) = x^2 + x — 2.
Формула умножения многочленов: чтобы умножить два многочлена, нужно умножить каждый член первого многочлена на каждый член второго многочлена, а затем сложить полученные произведения. Например, (3x^2 + 2x + 1) * (2x^2 + x + 3) = 6x^4 + 5x^3 + 4x^2 + 5x + 3.
Формула деления многочленов: чтобы разделить один многочлен на другой, нужно использовать алгоритм деления столбиком или формулу синтетического деления. Например, (3x^2 + 2x + 1) / (x + 1) = 3x — 1, остаток: 2.
Знание этих формул позволяет эффективно работать с многочленами и решать различные задачи, связанные с алгеброй и анализом функций.
Раздел 2: Геометрия

В разделе «Геометрия» для успешной подготовки к ЕГЭ по математике необходимо усвоить основные геометрические понятия и формулы, а также научиться применять их в задачах разной сложности.
Одной из важных формул в геометрии является формула площади треугольника. Площадь треугольника можно найти, зная его высоту и основание, по формуле: S = (1/2) * a * h, где S — площадь треугольника, a — длина основания, h — высота треугольника.
Еще одной важной формулой является формула площади круга. Площадь круга можно найти, зная его радиус, по формуле: S = П * r^2, где S — площадь круга, П — математическая константа, примерно равная 3.14, r — радиус круга.
Формулы для нахождения объема и площади поверхности прямоугольного параллелепипеда также очень полезны. Объем прямоугольного параллелепипеда можно найти, зная его длину, ширину и высоту, по формуле: V = a * b * h, где V — объем параллелепипеда, a — длина, b — ширина, h — высота. Площадь поверхности прямоугольного параллелепипеда можно найти по формуле: S = 2(ab + ah + bh).
Это лишь некоторые из формул, которые необходимо знать и уметь применять в задачах геометрии. Более подробно ознакомиться с ними и другими формулами можно в учебниках по математике или на специализированных сайтах.
Формулы для вычисления площади и объема
При решении задач по математике, особенно на ЕГЭ, часто требуется вычислить площадь или объем различных геометрических фигур. Для этих целей существуют специальные формулы, которые позволяют с легкостью найти нужное значение.
Ниже приведены некоторые из самых важных формул для вычисления площади и объема:
- Площадь прямоугольника: S = a * b, где a и b — длины сторон прямоугольника.
- Площадь треугольника: S = (a * h) / 2, где a — длина основания треугольника, h — высота, опущенная на это основание.
- Площадь круга: S = π * r^2, где π — математическая константа, равная примерно 3,14, r — радиус круга.
- Объем параллелепипеда: V = a * b * h, где a, b и h — длины трех ребер параллелепипеда.
- Объем цилиндра: V = π * r^2 * h, где r — радиус основания цилиндра, h — высота цилиндра.
Это лишь некоторые из формул, которые могут пригодиться при решении задач на ЕГЭ по математике. Запомните их и применяйте в своих расчетах, чтобы упростить задачу и получить правильный ответ.
Раздел 3: Тригонометрия
В тригонометрии выделяют 6 основных тригонометрических функций: синус, косинус, тангенс, котангенс, секанс и косеканс. Они определяются отношением сторон прямоугольного треугольника и позволяют вычислять значения углов и сторон треугольников.
Формулы для вычисления значений тригонометрических функций могут быть представлены в виде таблицы:
Тригонометрическая функцияОпределениеЗначения в обычных углах
| Синус (sin) | Противоположная сторона / Гипотенуза | От -1 до 1 |
| Косинус (cos) | Прилежащая сторона / Гипотенуза | От -1 до 1 |
| Тангенс (tg) | Противоположная сторона / Прилежащая сторона | Любое число |
| Котангенс (ctg) | Прилежащая сторона / Противоположная сторона | Любое число |
| Секанс (sec) | Гипотенуза / Прилежащая сторона | От 1 до бесконечности |
| Косеканс (cosec) | Гипотенуза / Противоположная сторона | От 1 до бесконечности |
Также в тригонометрии широко используются тригонометрические тождества, которые позволяют упростить выражения и решить сложные задачи. Некоторые из основных тригонометрических тождеств:
- Формула синуса: sin(A) = a / c
- Формула косинуса: cos(A) = b / c
- Формула тангенса: tg(A) = a / b
- Формула котангенса: ctg(A) = b / a
Знание тригонометрических формул и функций является важным для успешной сдачи экзамена по математике ЕГЭ и решения различных задач, связанных с геометрией и физикой.
Формулы для вычисления синуса, косинуса и тангенса
Формулы для вычисления синуса, косинуса и тангенса основываются на отношениях сторон в прямоугольном треугольнике. В прямоугольном треугольнике катеты обозначаются как a и b, а гипотенуза — как c.
- Формула для вычисления синуса: sin(α) = a/c
- Формула для вычисления косинуса: cos(α) = b/c
- Формула для вычисления тангенса: tan(α) = a/b
Здесь α — угол треугольника, а sin, cos и tan — тригонометрические функции синуса, косинуса и тангенса соответственно.
Эти формулы позволяют нам вычислять значения синуса, косинуса и тангенса для любого угла треугольника. Они также могут быть использованы для решения различных задач, связанных с геометрией и физикой.
Раздел 4: Вероятность и статистика
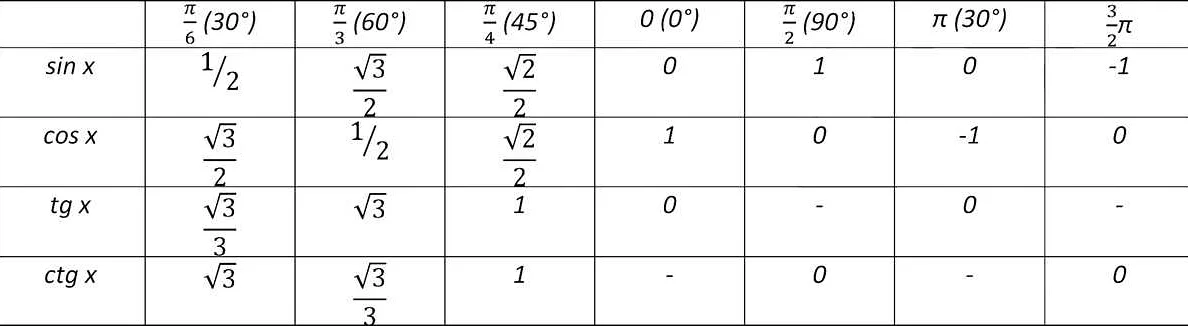
1. Вероятность
Вероятность – это численная характеристика, отражающая степень уверенности в наступлении или ненаступлении определенного события. Она измеряется от 0 до 1, где 0 – событие невозможно, а 1 – событие обязательно.
2. Формула для вычисления вероятности
Вероятность события A обозначается P(A) и вычисляется по формуле:
| P(A) = | количество благоприятных исходов | |
| количество возможных исходов |
3. Статистика
Статистика – наука, изучающая методы сбора, обработки и анализа данных. Она позволяет получить информацию о различных явлениях и процессах на основе наблюдений и экспериментов.
4. Среднее значение
Среднее значение – это численная характеристика, которая показывает общую закономерность или типичность данных. Оно вычисляется по формуле:
| Среднее значение = | сумма всех значений | |
| количество значений |
5. Дисперсия
Дисперсия – это численная характеристика, которая показывает разброс данных относительно их среднего значения. Она вычисляется по формуле:
| Дисперсия = | сумма квадратов разностей | |
| количество значений |
6. Корреляция
Корреляция – это численная характеристика, которая показывает степень взаимосвязи двух величин. Коэффициент корреляции принимает значения от -1 до 1, где -1 – полная обратная зависимость, 0 – отсутствие зависимости, 1 – полная прямая зависимость.
Это лишь некоторые из основных формул и понятий, связанных с вероятностью и статистикой. Знание этих формул и умение применять их в задачах помогут вам успешно справиться с соответствующими заданиями на ЕГЭ по математике.
Видео по теме:
Вопрос-ответ:
Какие формулы являются самыми важными для сдачи ЕГЭ по математике?
Самыми важными формулами для сдачи ЕГЭ по математике являются формулы для нахождения площади и периметра прямоугольника, квадрата и треугольника, формула Герона для нахождения площади треугольника по длинам его сторон, формула для нахождения объема и площади поверхности цилиндра, формула для нахождения площади круга и длины окружности, формулы для нахождения синуса, косинуса и тангенса угла, формула косинусов и формула синусов для нахождения длин сторон треугольника и его углов.
Как применить формулу Герона для нахождения площади треугольника по длинам его сторон?
Для применения формулы Герона необходимо знать длины всех сторон треугольника. Формула выглядит следующим образом: S = √(p(p-a)(p-b)(p-c)), где S — площадь треугольника, p — полупериметр треугольника (p = (a+b+c)/2), a, b, c — длины сторон треугольника. Подставляя значения длин сторон в формулу, можно вычислить площадь треугольника.
Какая формула используется для нахождения площади круга?
Формула для нахождения площади круга выглядит следующим образом: S = πr², где S — площадь круга, π — математическая константа, примерное значение которой равно 3.14, r — радиус круга. Для нахождения площади круга необходимо знать значение радиуса и подставить его в формулу.
Как применить формулу синусов для нахождения длин сторон треугольника и его углов?
Формула синусов позволяет находить длины сторон треугольника и его углы при известных значениях сторон и соответствующих им углов. Формула выглядит следующим образом: a/sinA = b/sinB = c/sinC, где a, b, c — длины сторон треугольника, A, B, C — соответствующие углы. Для применения формулы необходимо знать значения двух сторон и угла между ними или значения трех сторон. Подставляя значения в формулу, можно вычислить длины сторон и углы треугольника.
Формулы для вычисления вероятности событий

Ниже представлены основные формулы для вычисления вероятности:
ФормулаОписание
| 1. P(A) = n(A) / n(S) | Формула классической вероятности, где P(A) – вероятность наступления события A, n(A) – число благоприятных исходов, n(S) – общее число исходов. |
| 2. P(A ∪ B) = P(A) + P(B) — P(A ∩ B) | Формула вероятности объединения событий A и B, где P(A ∪ B) – вероятность наступления хотя бы одного из событий A или B, P(A ∩ B) – вероятность наступления событий A и B одновременно. |
| 3. P(A|B) = P(A ∩ B) / P(B) | Формула условной вероятности, где P(A|B) – вероятность наступления события A при условии, что событие B уже произошло, P(A ∩ B) – вероятность наступления событий A и B одновременно, P(B) – вероятность наступления события B. |
Знание данных формул позволяет более точно оценить вероятность наступления различных событий и проводить анализ вероятностных моделей.
Раздел 5: Логарифмы
Одной из самых важных формул, связанных с логарифмами, является формула для вычисления значения логарифма по основанию a:
loga(x) = y ⇔ ay = x
Эта формула позволяет найти значение логарифма, если известны основание a и число x.
Еще одной важной формулой является формула изменения основания логарифма:
loga(b) = logc(b) / logc(a)
Эта формула позволяет переводить логарифмы с одного основания на другое.
Одно из применений логарифмов – решение уравнений с экспонентами. Например, для решения уравнения ax = b можно использовать логарифмы:
x = loga(b)
Логарифмы также широко применяются в статистике для анализа данных. Например, логарифмические шкалы позволяют визуализировать данные с различными порядками величин.
Знание формул и свойств логарифмов позволяет эффективно решать задачи на ЕГЭ по математике и успешно справляться с другими математическими задачами в жизни и в научной работе.
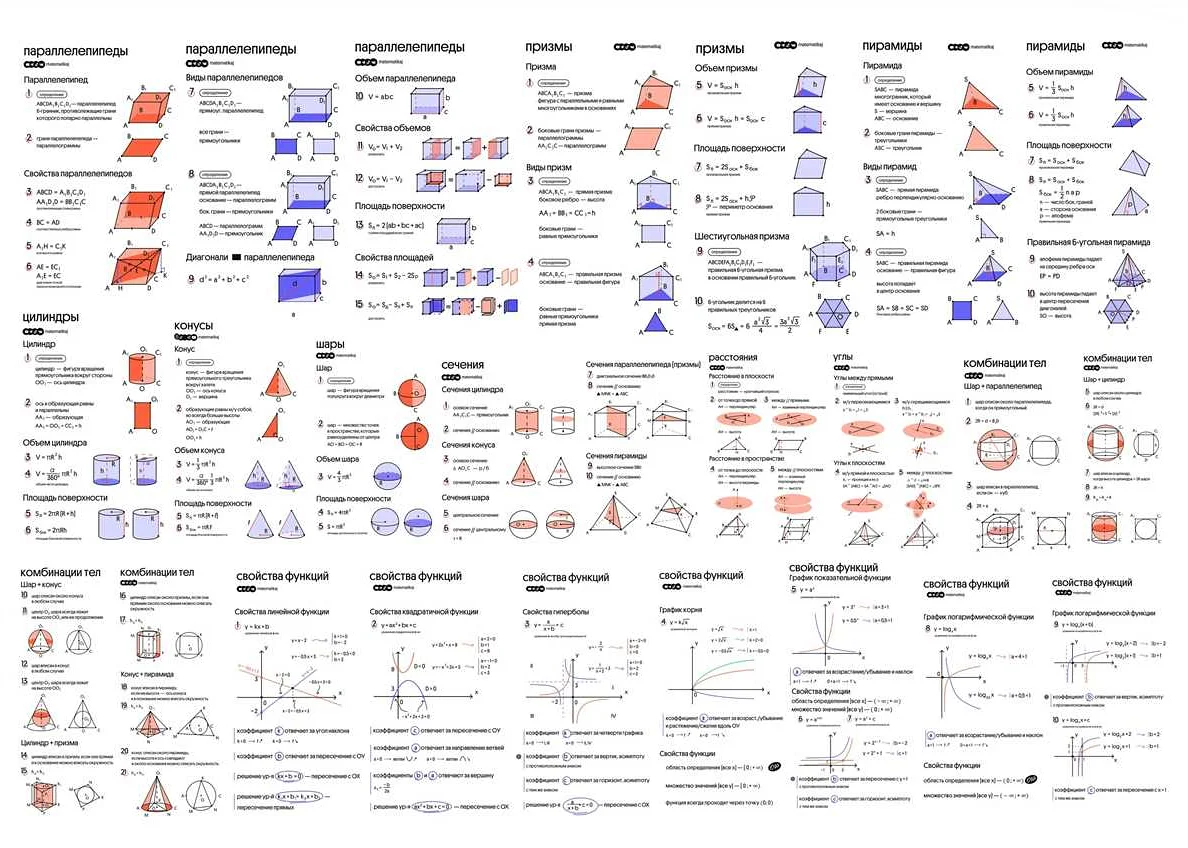


Статья очень полезная и информативная. Я всегда стараюсь быть в курсе всех формул для ЕГЭ по математике, чтобы успешно справиться с экзаменом. В статье указаны самые важные формулы, которые помогут мне в решении задач. Очень удобно, что рассмотрены как основные формулы, так и более сложные, чтобы я могла разобраться в них подробнее. Также в статье приведены примеры применения формул, которые помогут мне лучше понять и запомнить их. Спасибо автору за такую понятную и полезную статью! Теперь я гораздо увереннее в своих знаниях и готова к экзамену.
Эта статья очень полезная и информативная! Я совсем скоро сдаю ЕГЭ по математике, и эти формулы пригодятся мне на экзамене. Я благодарна автору за то, что он собрал все самые важные формулы в одном месте и подробно объяснил, как их применять. Теперь я точно знаю, что такое формула Герона и как ее использовать для решения задач на площадь треугольника. А формула Бинома Ньютона стала для меня настоящим спасением при работе с многочленами. Я обязательно воспользуюсь этой информацией при подготовке к экзамену. Большое спасибо за полезную статью!