Формулы которые понадобятся на огэ по математике 2021

В данной статье представлены основные формулы и правила, которые необходимо знать и уметь применять для успешной подготовки к ОГЭ по математике в 2021 году. Изучение этих формул поможет ученикам эффективно решать задачи и достичь высоких результатов на экзамене.

Олимпиада Государственной экзаменационной комиссии (ОГЭ) по математике является одним из самых важных испытаний для школьников. Она проверяет их знания и навыки в области математики, а также способность применять математические формулы для решения различных задач.

Важно знать основные формулы, чтобы успешно справиться с заданиями ОГЭ. Некоторые формулы являются базовыми и должны быть запомнены наизусть, другие могут быть выведены из базовых формул в процессе решения задачи. В этой статье мы представляем список необходимых математических формул для подготовки к ОГЭ по математике 2021 года.

Формулы для ОГЭ по математике включают в себя арифметические, геометрические и алгебраические формулы. Они помогают учащимся решать задачи, связанные с простыми и сложными вычислениями, работать с графиками, находить площади и объемы фигур, а также решать уравнения и неравенства.

Например, одной из базовых арифметических формул является формула для вычисления площади прямоугольника: S = a * b, где S — площадь, a — длина стороны, b — ширина стороны. Эта формула может быть использована для решения задач о площади прямоугольников различных размеров.

Помимо арифметических формул, важно знать и геометрические формулы. Например, формула для вычисления площади треугольника: S = (a * h) / 2, где S — площадь, a — длина основания, h — высота треугольника. Эта формула позволяет находить площади треугольников с разными основаниями и высотами.

Знание этих и других формул поможет учащимся подготовиться к ОГЭ по математике и уверенно решать задачи на экзамене. Практика применения формул в различных задачах поможет развить логическое мышление и навыки решения математических задач, что важно для успешной сдачи ОГЭ и будущей работы с математикой.

Арифметические операции и приоритеты

Приоритет операций определяет порядок выполнения арифметических операций в выражении. Операции с более высоким приоритетом выполняются раньше операций с более низким приоритетом.

Приоритеты операций в математике следующие:

1. Скобки — операции внутри скобок выполняются первыми.
2. Умножение и деление — эти операции имеют одинаковый приоритет и выполняются перед операциями сложения и вычитания.
3. Сложение и вычитание — эти операции имеют одинаковый приоритет и выполняются после операций умножения и деления.

Например, в выражении 2 + 3 * 5, сначала производится умножение 3 * 5, а затем сложение 2 + 15, что дает результат 17.

Для изменения порядка выполнения операций можно использовать скобки. Например, в выражении (2 + 3) * 5, сначала выполняется сложение в скобках 2 + 3, а затем умножение на 5, что дает результат 25.

При решении задач и составлении выражений важно учитывать приоритеты операций, чтобы получить правильный результат.

Формулы для работы с прямыми и плоскостями

Для решения задач, связанных с прямыми и плоскостями, необходимо знать основные формулы. В данном разделе представлен список формул, которые помогут вам успешно справиться с такими заданиями на ОГЭ по математике.

Уравнение прямой по координатам двух точек:

Если даны координаты двух точек A(x1, y1) и B(x2, y2), то уравнение прямой, проходящей через эти точки, можно найти по следующей формуле:

y — y1 = (y2 — y1) / (x2 — x1) * (x — x1)

Уравнение прямой в общем виде:

Если известны коэффициенты a, b и c, то уравнение прямой можно записать в виде:

ax + by + c = 0

Угловой коэффициент прямой:

Угловой коэффициент прямой можно найти по следующей формуле:

k = (y2 — y1) / (x2 — x1)

Уравнение плоскости по координатам трех точек:

Если даны координаты трех точек A(x1, y1, z1), B(x2, y2, z2) и C(x3, y3, z3), то уравнение плоскости, проходящей через эти точки, можно найти по следующей формуле:

ax + by + cz + d = 0

Запомните эти формулы и применяйте их при решении задач, связанных с прямыми и плоскостями. Успехов вам на ОГЭ по математике!

Геометрические фигуры и их свойства

В таблице ниже приведены основные геометрические фигуры и их свойства:

ФигураОписаниеСвойства

Треугольник	Фигура, образованная тремя отрезками, соединяющими три точки, не лежащие на одной прямой.	— Сумма внутренних углов треугольника равна 180 градусам. — Сумма длин двух сторон треугольника всегда больше длины третьей стороны. — Высота треугольника — перпендикуляр, опущенный из вершины на противоположную сторону. — Медиана треугольника — отрезок, соединяющий вершину с серединой противоположной стороны. — Биссектриса треугольника — отрезок, делящий угол на два равных по величине угла. — Окружность, вписанная в треугольник, касается всех трех сторон. — Окружность, описанная около треугольника, проходит через все три вершины.
Квадрат	Фигура, у которой все четыре стороны равны между собой и все углы прямые.	— Площадь квадрата равна квадрату длины его стороны. — Периметр квадрата равен сумме длин его сторон. — Диагональ квадрата — отрезок, соединяющий противоположные вершины квадрата. — Квадрат является прямоугольником, ромбом и параллелограммом.
Круг	Фигура, образованная всеми точками плоскости, равноудаленными от одной точки — центра круга.	— Площадь круга равна произведению квадрата радиуса на число пи (приближенно 3,14). — Длина окружности равна произведению диаметра на число пи. — Радиус круга — отрезок, соединяющий центр круга с любой точкой на его границе. — Диаметр круга — отрезок, соединяющий две точки на границе круга, проходящие через его центр. — Сектор круга — фигура, ограниченная двумя радиусами и дугой окружности. — Сегмент круга — фигура, ограниченная дугой окружности и хордой.

Формулы для работы с уравнениями и неравенствами

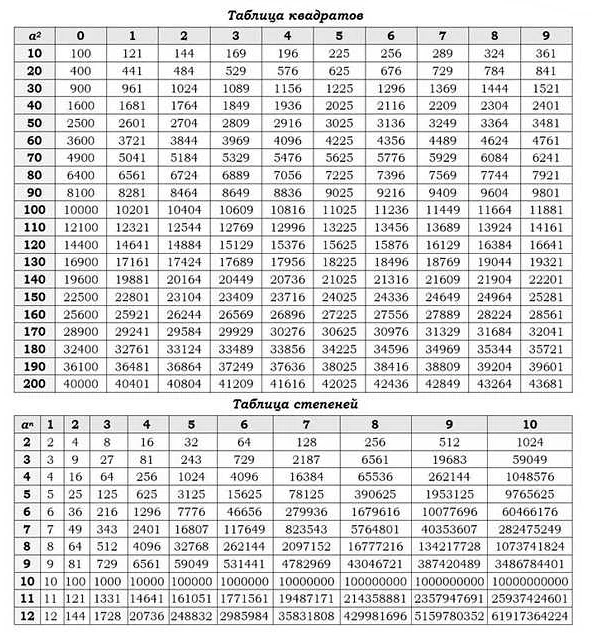
Во время выполнения заданий по математике на ОГЭ важно знать основные формулы для работы с уравнениями и неравенствами. Эти формулы позволяют вычислять и находить значения переменных, решать уравнения и искать корни.

Ниже приведены основные формулы для работы с уравнениями:

Формула дискриминанта:

Для квадратного уравнения ax^2 + bx + c = 0, где a, b и c — коэффициенты, дискриминант можно вычислить по формуле:

D = b^2 — 4ac

Формула корней квадратного уравнения:

Если дискриминант D больше нуля, то уравнение имеет два различных корня:

x1 = (-b + √D) / 2a

x2 = (-b — √D) / 2a

Если дискриминант равен нулю, то уравнение имеет один корень:

x = -b / (2a)

Если дискриминант меньше нуля, то уравнение не имеет действительных корней.

Формула корней линейного уравнения:

Линейное уравнение ax + b = 0 имеет единственный корень:

x = -b / a

Для работы с неравенствами также используются специальные формулы:

Формула смены знака:

Если в уравнении имеется знак неравенства (, ≥), то при переносе одного из членов в другую часть уравнения знак неравенства меняется на противоположный.

Формула сокращенного умножения:

Если при умножении или делении обе стороны неравенства на одно и то же положительное число, то знак неравенства не меняется.

Знание этих формул поможет вам успешно решать задачи, связанные с уравнениями и неравенствами на ОГЭ по математике.

Пространственная геометрия и векторы

В данном разделе рассматриваются основные понятия и формулы, связанные с пространственной геометрией и векторами:

• Скалярное произведение векторов
• Векторное произведение векторов
• Смешанное произведение векторов
• Угол между векторами
• Проекция вектора на ось
• Коллинеарные векторы
• Компланарные векторы
• Скалярное уравнение плоскости
• Векторное уравнение прямой
• Уравнение плоскости в пространстве
• Уравнение прямой в пространстве

Знание данных понятий и формул позволяет решать задачи, связанные с геометрией и векторами в трехмерном пространстве. Эти знания необходимы для успешной сдачи ОГЭ по математике. При подготовке к экзамену рекомендуется усвоить эти формулы и научиться применять их в задачах различной сложности.

Формулы для работы с функциями и графиками

Для удобной работы с функциями и графиками на ОГЭ по математике важно знать основные формулы, которые помогут решить задачи данной темы. Вот несколько основных формул:

• Уравнение прямой вида y = kx + b
• Уравнение параболы вида y = ax^2 + bx + c
• Уравнение окружности вида (x — a)^2 + (y — b)^2 = r^2
• Формула расчета расстояния между двумя точками на плоскости: d = √((x2 — x1)^2 + (y2 — y1)^2)
• Формула нахождения координат вершины параболы: x = -b/2a, y = f(x)
• Формула нахождения координат точки пересечения графиков двух функций: решение системы уравнений

Зная эти формулы, вы сможете решать задачи на построение графиков функций, нахождение координат точек и другие задачи, связанные с функциями и графиками.

Не забывайте тренироваться на решении задач и использовании данных формул, чтобы успешно справиться с этой темой на ОГЭ по математике.

Статистика и вероятность

Вероятность — наука, изучающая случайные явления и их вероятности. Вероятность определяется как отношение числа благоприятных исходов к общему числу исходов. Основные понятия в теории вероятности включают события, вероятностное пространство, условную вероятность, независимость событий и формулы для расчета вероятностей.

Основные формулы:

1. Формула сложения вероятностей: P(A ∪ B) = P(A) + P(B) — P(A ∩ B)

2. Формула умножения вероятностей: P(A ∩ B) = P(A) * P(B|A)

3. Формула полной вероятности: P(A) = P(A|B1) * P(B1) + P(A|B2) * P(B2) + … + P(A|Bn) * P(Bn)

4. Формула Байеса: P(Bi|A) = (P(A|Bi) * P(Bi)) / P(A)

Кроме того, для работы с выборками и расчета характеристик используются следующие формулы:

1. Среднее значение: M = (x1 + x2 + … + xn) / n

2. Медиана: Me = x((n+1)/2) или Me = (x(n/2) + x(n/2+1)) / 2 (для четного n)

3. Мода: Mo — наиболее часто встречающееся значение

4. Дисперсия: D = ((x1 — M)^2 + (x2 — M)^2 + … + (xn — M)^2) / n

Эти формулы помогут вам решать задачи по статистике и вероятности на ОГЭ по математике.

Тригонометрия и геометрические преобразования

Одной из основных формул тригонометрии является формула синуса, которая позволяет найти длину стороны треугольника по заданным углам и сторонам:

a/sin(A) = b/sin(B) = c/sin(C)

Формула косинуса также широко используется в тригонометрии. Она позволяет найти длину стороны треугольника по заданным углам и сторонам:

a^2 = b^2 + c^2 — 2bc*cos(A)

Формула тангенса позволяет найти тангенс угла треугольника по заданным сторонам:

tan(A) = a/b

Геометрические преобразования включают поворот, отражение, симметрию и сжатие. Формулы для этих преобразований могут быть записаны следующим образом:

Поворот:

x’ = x*cos(α) — y*sin(α)

y’ = x*sin(α) + y*cos(α)

Отражение:

x’ = -x

y’ = -y

Симметрия:

x’ = -x

y’ = -y

Сжатие:

x’ = ax

y’ = by

Знание и умение применять эти формулы поможет вам успешно справиться с задачами по тригонометрии и геометрии на ОГЭ по математике.

Видео по теме:

Какие формулы нужно знать для ОГЭ по математике в 2021 году?

Для ОГЭ по математике в 2021 году необходимо знать следующие формулы: формулы для вычисления площади и периметра геометрических фигур, формулы для вычисления объема и площади поверхности геометрических тел, формулы для вычисления процента и процентного соотношения, формулы для вычисления среднего арифметического и медианы числового ряда, формулы для вычисления площади треугольника, формулы для решения уравнений и неравенств, формулы для вычисления вероятности и т.д.

Какая формула используется для вычисления площади треугольника?

Формула для вычисления площади треугольника: S = (a * h) / 2, где S — площадь треугольника, a — длина основания треугольника, h — высота, опущенная на основание треугольника.

Какую формулу использовать для вычисления объема параллелепипеда?

Формула для вычисления объема параллелепипеда: V = a * b * h, где V — объем параллелепипеда, a — длина, b — ширина и h — высота параллелепипеда.

Какую формулу использовать для вычисления процента?

Формула для вычисления процента: P = (p * 100) / m, где P — процент, p — часть от целого, m — целое.

Какую формулу использовать для вычисления среднего арифметического?

Формула для вычисления среднего арифметического: M = (x1 + x2 + … + xn) / n, где M — среднее арифметическое, x1, x2, …, xn — числа, n — количество чисел.

Какая формула нужна для вычисления площади прямоугольника на ОГЭ по математике в 2021 году?

Для вычисления площади прямоугольника на ОГЭ по математике в 2021 году используется формула: S = a * b, где a и b — длины сторон прямоугольника. Для подсчета площади необходимо умножить длину одной стороны на длину другой стороны. Эта формула применима только к прямоугольникам, у которых все углы прямые.