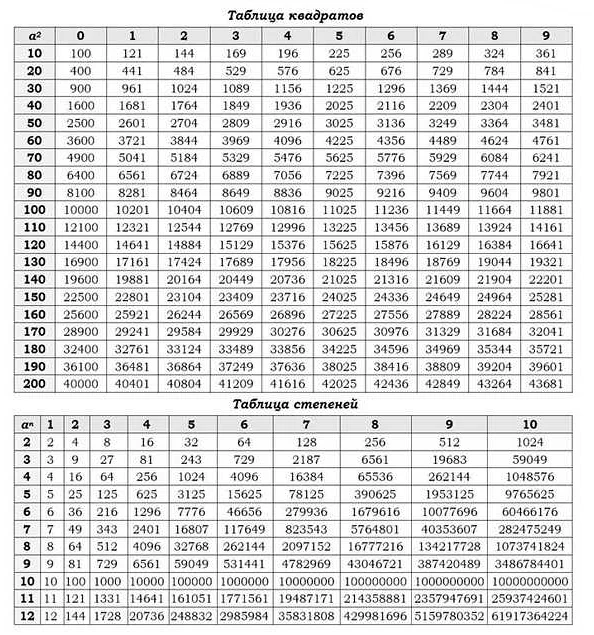
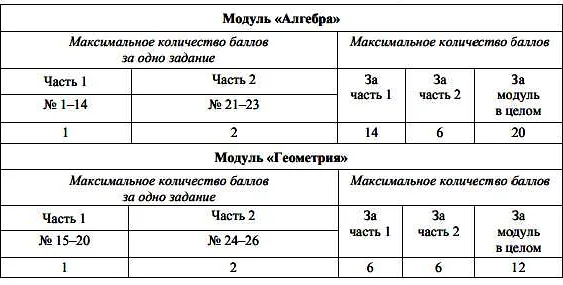
Формулы для огэ по математике 2021 которые будут на экзамене

Подготовка к ОГЭ по математике 2021: список формул, которые будут включены в экзамен. Узнайте, какие формулы необходимо знать для успешной сдачи ОГЭ по математике в 2021 году.

Каждый год выпускники 9-х классов в России сдают обязательный экзамен по математике в рамках ОГЭ. В этом году учащимся предстоит столкнуться с множеством различных задач и вопросов, в которых пригодятся определенные математические формулы. Знание этих формул является ключевым аспектом успешной подготовки к экзамену.

Согласно официальным правилам, на ОГЭ разрешено использовать список разрешенных формул. Это означает, что учащимся необходимо знать и уметь применять определенные математические формулы, чтобы решать задачи и демонстрировать свои знания. Список формул для ОГЭ по математике обычно содержит основные формулы из различных разделов математики, таких как геометрия, алгебра и арифметика.

Некоторые из наиболее важных формул, которые могут понадобиться на ОГЭ по математике в 2021 году, включают формулы для вычисления площади и периметра различных фигур, формулы для решения уравнений и систем уравнений, формулу для вычисления процентов и другие ключевые математические соотношения. Знание и правильное применение этих формул поможет ученикам эффективно решать задачи и достичь высоких результатов на экзамене.

Арифметические операции с числами:

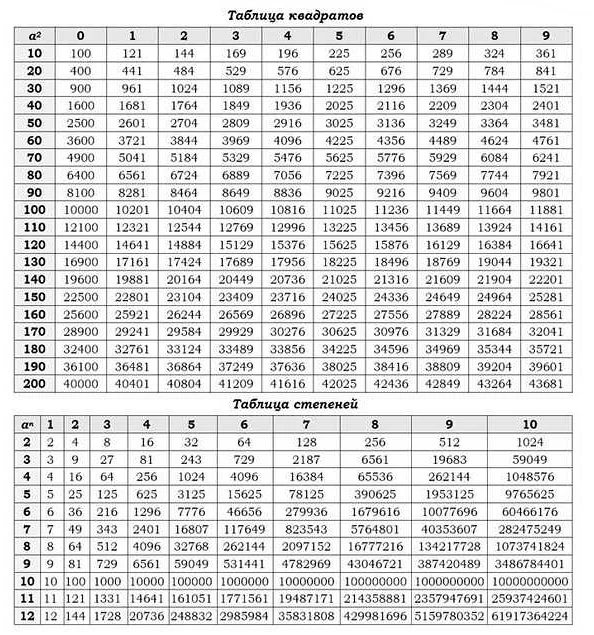
На экзамене по математике ОГЭ 2021 года потребуется знание основных арифметических операций с числами. Ниже представлен список формул, которые могут встретиться на экзамене:

1. Сложение: a + b = c. Чтобы сложить два числа, нужно их прибавить.

2. Вычитание: a — b = c. Чтобы вычесть одно число из другого, нужно из первого числа вычесть второе число.

3. Умножение: a * b = c. Чтобы умножить два числа, нужно первое число умножить на второе число.

4. Деление: a / b = c. Чтобы разделить одно число на другое, нужно первое число поделить на второе число.

5. Возведение в степень: a^b = c. Чтобы возвести число в степень, нужно число умножить само на себя нужное количество раз.

6. Извлечение корня: sqrt(a) = b. Чтобы найти корень из числа, нужно найти такое число, которое при возведении в квадрат даст исходное число.

Знание этих формул поможет вам успешно справиться с заданиями по арифметике на ОГЭ по математике. При решении задач не забывайте использовать данные формулы!

Геометрические фигуры и формулы для расчетов:

На ОГЭ по математике в 2021 году могут быть представлены следующие геометрические фигуры и формулы:

• Площадь круга: S = πr², где r — радиус круга, π (пи) примерно равно 3,14.
• Длина окружности: L = 2πr, где r — радиус круга, π (пи) примерно равно 3,14.
• Площадь прямоугольника: S = ab, где a и b — длины сторон прямоугольника.
• Периметр прямоугольника: P = 2(a + b), где a и b — длины сторон прямоугольника.
• Площадь треугольника: S = 0.5ah, где a — длина основания треугольника, h — высота треугольника.
• Периметр треугольника: P = a + b + c, где a, b и c — длины сторон треугольника.
• Площадь квадрата: S = a², где a — длина стороны квадрата.
• Периметр квадрата: P = 4a, где a — длина стороны квадрата.

Запомни эти формулы и используй их для решения задач по геометрии на экзамене ОГЭ!

Уравнения и системы уравнений:

На экзамене ОГЭ по математике 2021 года возможно появление следующих формул, связанных с уравнениями и системами уравнений:

1. Формула дискриминанта для квадратного уравнения: D = b^2 — 4ac, где a, b и c — коэффициенты квадратного уравнения ax^2 + bx + c = 0;
2. Формула корней квадратного уравнения: x = (-b ± √D) / (2a), где a, b и c — коэффициенты квадратного уравнения ax^2 + bx + c = 0;
3. Формула суммы корней квадратного уравнения: x₁ + x₂ = -b / a, где a, b и c — коэффициенты квадратного уравнения ax^2 + bx + c = 0;
4. Формула произведения корней квадратного уравнения: x₁ * x₂ = c / a, где a, b и c — коэффициенты квадратного уравнения ax^2 + bx + c = 0;
5. Формула суммы корней кубического уравнения: x₁ + x₂ + x₃ = -b / a, где a, b и c — коэффициенты кубического уравнения ax^3 + bx^2 + cx + d = 0;
6. Формула произведения корней кубического уравнения: x₁ * x₂ * x₃ = -d / a, где a, b, c и d — коэффициенты кубического уравнения ax^3 + bx^2 + cx + d = 0;
7. Формула Виета для квадратного уравнения: x₁ + x₂ = -b / a и x₁ * x₂ = c / a, где a, b и c — коэффициенты квадратного уравнения ax^2 + bx + c = 0;
8. Формула Виета для кубического уравнения: x₁ + x₂ + x₃ = -b / a, x₁ * x₂ + x₁ * x₃ + x₂ * x₃ = c / a и x₁ * x₂ * x₃ = -d / a, где a, b, c и d — коэффициенты кубического уравнения ax^3 + bx^2 + cx + d = 0;
9. Формула суммы корней системы уравнений: x + y = -p, где x и y — корни системы уравнений, а p — сумма корней;
10. Формула произведения корней системы уравнений: xy = q, где x и y — корни системы уравнений, а q — произведение корней.

Проценты и доли:

Основные формулы, которые следует знать:

1. Процент: процент от числа можно найти, умножив число на соответствующую десятичную долю процента. Формула выглядит следующим образом:

Процент = Число × Доля процента

2. Доля: долю можно найти, разделив одно число на другое и умножив результат на 100%. Формула выглядит следующим образом:

Доля = (Число / Общее число) × 100%

3. Изменение доли: для нахождения изменения доли нужно вычислить разность между двумя долями и разделить ее на изначальную долю. Формула выглядит следующим образом:

Изменение доли = (Новая доля — Изначальная доля) / Изначальная доля × 100%

Зная эти формулы, можно успешно решать задачи, связанные с процентами и долями на экзамене по математике.

Статистика и вероятность:

Выборочное среднее — это среднее значение числовой последовательности или группы чисел.

Медиана — это значение, которое делит выборку на две равные части. Если выборка состоит из нечетного числа элементов, медиана будет являться средним значением. В случае четного числа элементов, медиана будет являться средним арифметическим двух средних значений.

Мода — это значение или значения, которые наиболее часто встречаются в выборке.

Дисперсия — это мера разброса значений в выборке относительно их среднего значения. Она показывает, насколько данные отклоняются от своего среднего значения.

Стандартное отклонение — это квадратный корень из дисперсии и используется для измерения разброса значений относительно их среднего значения.

Вероятность — это мера того, насколько вероятно возникновение определенного события. В контексте ОГЭ по математике, вероятность включает в себя изучение основных понятий, таких как элементарное событие, пространство элементарных событий, случайная величина, событие, условная вероятность и независимость событий.

Элементарное событие — это самое простое, неделимое событие, которое может произойти в эксперименте.

Пространство элементарных событий — это множество всех возможных элементарных событий в эксперименте.

Случайная величина — это величина, которая принимает определенные значения в зависимости от результата эксперимента.

Событие — это набор элементарных событий. Оно может включать одно или несколько элементарных событий.

Условная вероятность — это вероятность наступления одного события при условии, что другое событие уже произошло.

Независимость событий — это свойство двух событий, при котором наступление одного события не зависит от наступления другого события.

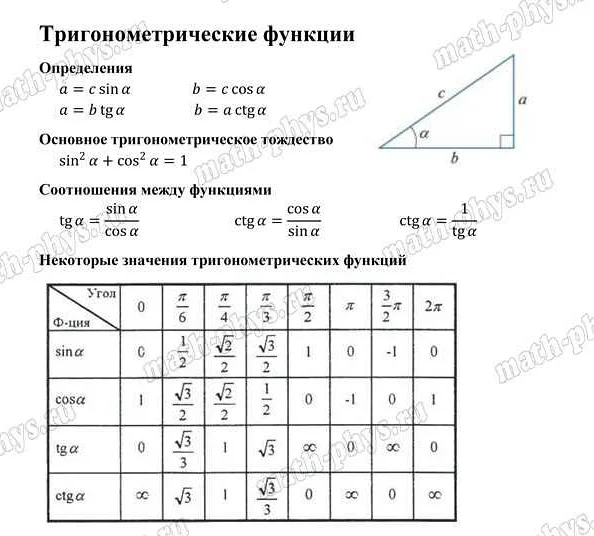
Тригонометрические функции:

На ОГЭ по математике может быть несколько формул, связанных с тригонометрическими функциями:

• Теорема Пифагора: a^2 + b^2 = c^2, где a и b — катеты прямоугольного треугольника, c — гипотенуза.
• Определение тригонометрических функций: в прямоугольном треугольнике с углом α против стороны a справедливы следующие соотношения:
  • Синус угла α: sinα = a / c
  • Косинус угла α: cosα = b / c
  • Тангенс угла α: tgα = a / b
  • Котангенс угла α: ctgα = b / a
• Соотношение между тригонометрическими функциями:
  • Тангенс угла: tgα = sinα / cosα
  • Котангенс угла: ctgα = cosα / sinα
  • Секанс угла: secα = 1 / cosα
  • Косеканс угла: cscα = 1 / sinα

Знание тригонометрических функций и их свойств позволяет решать различные задачи, связанные с измерением углов и расчетом сторон прямоугольных треугольников.

Формулы для работы с прямоугольными треугольниками:

ФормулаОписание

Теорема Пифагора	В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Формула для вычисления гипотенузы	Гипотенуза прямоугольного треугольника равна квадратному корню из суммы квадратов длин катетов.
Формулы для вычисления катетов	Катет прямоугольного треугольника равен квадратному корню из разности квадрата длины гипотенузы и квадрата длины другого катета.
Формулы для вычисления площади	Площадь прямоугольного треугольника равна половине произведения длин катетов.
Формула для вычисления периметра	Периметр прямоугольного треугольника равен сумме длин всех его сторон.

Зная эти формулы, можно легко решать задачи связанные с прямоугольными треугольниками на экзамене по математике ОГЭ.

Формулы для работы с окружностями:

2. Площадь круга: S = πr², где π — число пи (приближенно равно 3,14), r — радиус окружности.

3. Площадь сектора: Sсектора = (α/360°)πr², где α — центральный угол, который выражается в градусах, р — радиус окружности.

4. Длина дуги окружности: Lдуги = (α/360°)2πr, где α — центральный угол, который выражается в градусах, р — радиус окружности.

5. Формула касательной к окружности: y = kx + b, где k — коэффициент наклона касательной, b — свободный член уравнения, x и y — координаты точки, через которые проходит касательная.

Видео по теме:

Какая формула используется для вычисления площади прямоугольника на ОГЭ по математике?

Для вычисления площади прямоугольника на ОГЭ по математике используется формула: S = a * b, где a — длина прямоугольника, b — ширина прямоугольника.

Какая формула используется для вычисления площади треугольника на ОГЭ по математике?

Для вычисления площади треугольника на ОГЭ по математике используется формула: S = 0.5 * a * h, где a — основание треугольника, h — высота треугольника.

Какая формула используется для вычисления площади круга на ОГЭ по математике?

Для вычисления площади круга на ОГЭ по математике используется формула: S = π * r^2, где π — математическая константа, округленная до трех знаков после запятой (3,14), r — радиус круга.

Какая формула используется для вычисления длины окружности на ОГЭ по математике?

Для вычисления длины окружности на ОГЭ по математике используется формула: L = 2 * π * r, где π — математическая константа, округленная до трех знаков после запятой (3,14), r — радиус окружности.