Формулы которые пригодятся на егэ по математике профильный уровень
Содержимое
- 1 Формулы которые пригодятся на егэ по математике профильный уровень
- 1.1 Необходимость подготовки к ЕГЭ по математике профильного уровня
- 1.2 Раздел 1
- 1.3 Основные формулы геометрии
- 1.4 Раздел 2
- 1.5 Формулы для решения уравнений и неравенств
- 1.6 Раздел 3
- 1.7 Формулы для работы с функциями
- 1.8 Раздел 4
- 1.9 Формулы для работы с логарифмами и экспонентами
- 1.10 Вопрос-ответ:
- 1.10.0.1 Какие формулы необходимо знать для подготовки к ЕГЭ по математике профильного уровня?
- 1.10.0.2 Какие формулы трехгранника необходимо знать для подготовки к ЕГЭ по математике профильного уровня?
- 1.10.0.3 Какие формулы тригонометрии необходимо знать для подготовки к ЕГЭ по математике профильного уровня?
- 1.10.0.4 Какие формулы для работы с функциями необходимо знать для подготовки к ЕГЭ по математике профильного уровня?
- 1.10.0.5 Какие еще формулы необходимо знать для подготовки к ЕГЭ по математике профильного уровня, кроме указанных выше?
- 1.10.0.6 Какие формулы нужно знать для подготовки к ЕГЭ по математике профильного уровня?
- 1.10.0.7 Какие формулы нужно знать для решения задач на геометрию в ЕГЭ по математике профильного уровня?
- 1.11 Раздел 5
- 1.12 Видео по теме:
В данной статье представлены полезные формулы и советы, которые помогут подготовиться к экзамену ЕГЭ по математике профильного уровня. Наши рекомендации позволят быстро восстановить навыки решения задач, освежить память по ключевым темам и повысить шансы на успешную сдачу экзамена.
ЕГЭ по математике — это один из самых важных экзаменов для выпускников школ, планирующих поступление в вузы. Чтобы успешно справиться с этим испытанием, необходимо хорошо подготовиться. Одним из основных компонентов подготовки является изучение и понимание формул, которые могут встретиться в заданиях ЕГЭ.
Формулы играют важную роль в решении задач по математике. Они помогают упростить вычисления, найти решение и проверить его правильность. Некоторые формулы необходимо запомнить наизусть, а некоторые можно вывести или использовать подсказки, чтобы сократить время на решение задачи.
В подготовке к ЕГЭ по математике профильного уровня важно освоить формулы по разным темам: алгебра, геометрия, тригонометрия и другие. Кроме того, необходимо уметь применять эти формулы в различных ситуациях и задачах.
В данной статье мы рассмотрим некоторые основные формулы, которые могут встретиться на ЕГЭ по математике профильного уровня. Ознакомившись с ними и научившись применять, вы сможете повысить свои шансы на успешное сдачу экзамена.
Необходимость подготовки к ЕГЭ по математике профильного уровня

Для подготовки к ЕГЭ по математике профильного уровня необходимы знания и навыки, которые выходят за рамки программы обычной средней школы. Как правило, на экзамене представлены сложные задачи, требующие глубокого понимания математических концепций и умения применять их в различных контекстах.
Подготовка к ЕГЭ по математике профильного уровня помогает ученикам закрепить и углубить свои знания, а также научиться применять их на практике. Кроме того, она позволяет развить логическое мышление, аналитические и проблемно-ориентированные навыки, которые могут быть полезными во многих сферах жизни.
Подготовка к ЕГЭ по математике профильного уровня также помогает ученикам ознакомиться с форматом и структурой самого экзамена, что увеличивает шансы на успешное его сдачу. Знание типичных заданий и требований экзамена позволяет ученикам разработать эффективные стратегии решения задач и научиться эффективно использовать отведенное время.
В целом, подготовка к ЕГЭ по математике профильного уровня является важной ступенью на пути к успешной сдаче экзамена. Она помогает ученикам получить необходимые знания и навыки, а также уверенность в своих силах, что существенно повышает шансы на получение высокого балла и успешное поступление в университет или колледж.
Раздел 1
Формулы для подготовки к ЕГЭ по математике профильного уровня
В данном разделе представлены основные формулы, которые необходимо знать и уметь применять при подготовке к ЕГЭ по математике профильного уровня. Эти формулы позволят вам решать задачи с высокой эффективностью и точностью.
1. Формула площади прямоугольника:
S = a * b
где S — площадь, a — длина одной стороны, b — длина другой стороны.
2. Формула площади треугольника:
S = (1/2) * a * h
где S — площадь, a — длина основания, h — высота, опущенная на основание.
3. Формула площади круга:
S = π * r^2
где S — площадь, π — число пи (приближенно равно 3.14), r — радиус.
4. Формула объема параллелепипеда:
V = a * b * h
где V — объем, a — длина одной стороны основания, b — длина другой стороны основания, h — высота.
5. Формула объема шара:
V = (4/3) * π * r^3
где V — объем, π — число пи (приближенно равно 3.14), r — радиус.
6. Формула длины окружности:
L = 2 * π * r
где L — длина окружности, π — число пи (приближенно равно 3.14), r — радиус.
7. Формула бинома Ньютона:
(a + b)^n = C(n, 0) * a^n + C(n, 1) * a^(n-1) * b + … + C(n, n-1) * a * b^(n-1) + C(n, n) * b^n
где C(n, k) — биномиальный коэффициент, равный n! / (k! * (n-k)!), где n! — факториал числа n.
Запомните и пользуйтесь этими формулами, чтобы успешно справиться с задачами ЕГЭ по математике профильного уровня!
Основные формулы геометрии
ФигураФормула
| Площадь прямоугольника | S = a * b |
| Площадь квадрата | S = a^2 |
| Площадь треугольника | S = 0.5 * a * h |
| Площадь круга | S = π * r^2 |
| Объем параллелепипеда | V = a * b * h |
| Объем куба | V = a^3 |
| Объем цилиндра | V = π * r^2 * h |
Это лишь некоторые из основных формул геометрии. Важно запомнить и понимать их применение, а также уметь применять их в задачах ЕГЭ. Научитесь применять эти формулы и у вас будет хорошая база для успешной подготовки к экзамену.
Раздел 2

Второй раздел подготовки к ЕГЭ по математике профильного уровня включает в себя изучение различных формул и правил, которые помогут решать задачи и вычислять значения функций. Знание этих формул позволит решать задачи более эффективно и снизит вероятность ошибок.
Одной из важных формул в этом разделе является формула для нахождения площади треугольника. Она выглядит следующим образом:
| S = 0.5 * a * h |
где S — площадь треугольника, a — длина основания треугольника, h — высота треугольника, опущенная на основание.
Другой важной формулой является формула для нахождения площади круга:
| S = π * r2 |
где S — площадь круга, π — число пи (приближенно равное 3.14), r — радиус круга.
Также в этом разделе следует изучить формулу для нахождения суммы углов в многоугольнике:
| S = (n — 2) * 180 |
где S — сумма углов в многоугольнике, n — количество его сторон.
Это лишь некоторые из формул, которые следует запомнить при подготовке к ЕГЭ по математике профильного уровня. Они помогут в решении задач и вычислении значений функций.
Формулы для решения уравнений и неравенств

При подготовке к ЕГЭ по математике профильного уровня необходимо хорошо знать формулы для решения уравнений и неравенств. Они позволят вам эффективно решать различные задачи и получать правильные ответы.
Вот некоторые основные формулы:
- Формула дискриминанта: D = b² — 4ac
- Формула корней квадратного уравнения: x = (-b ± √D) / (2a)
- Формула корней кубического уравнения: x = ∛(−q/2 + √(q²/4 + p³/27)) + ∛(−q/2 − √(q²/4 + p³/27)) — a/3
- Формула корней квадратного неравенства: x ∈ [x₁, x₂], где x₁ и x₂ — корни квадратного уравнения
- Формула корней линейного неравенства: x ∈ (−∞, x₁) ∪ (x₂, +∞), где x₁ и x₂ — корни линейного уравнения
Помимо этих формул, стоит знать и другие способы решения уравнений и неравенств, такие как метод подстановки, метод интервалов, метод графиков и др. Комбинируя различные методы, вы сможете эффективно решать задачи на экзамене.
Решение уравнений и неравенств требует не только знания формул, но и умение анализировать и применять их в конкретных ситуациях. Поэтому регулярная практика и тренировка в решении различных типов задач помогут вам улучшить свои навыки и подготовиться к успешной сдаче ЕГЭ по математике профильного уровня.
Раздел 3
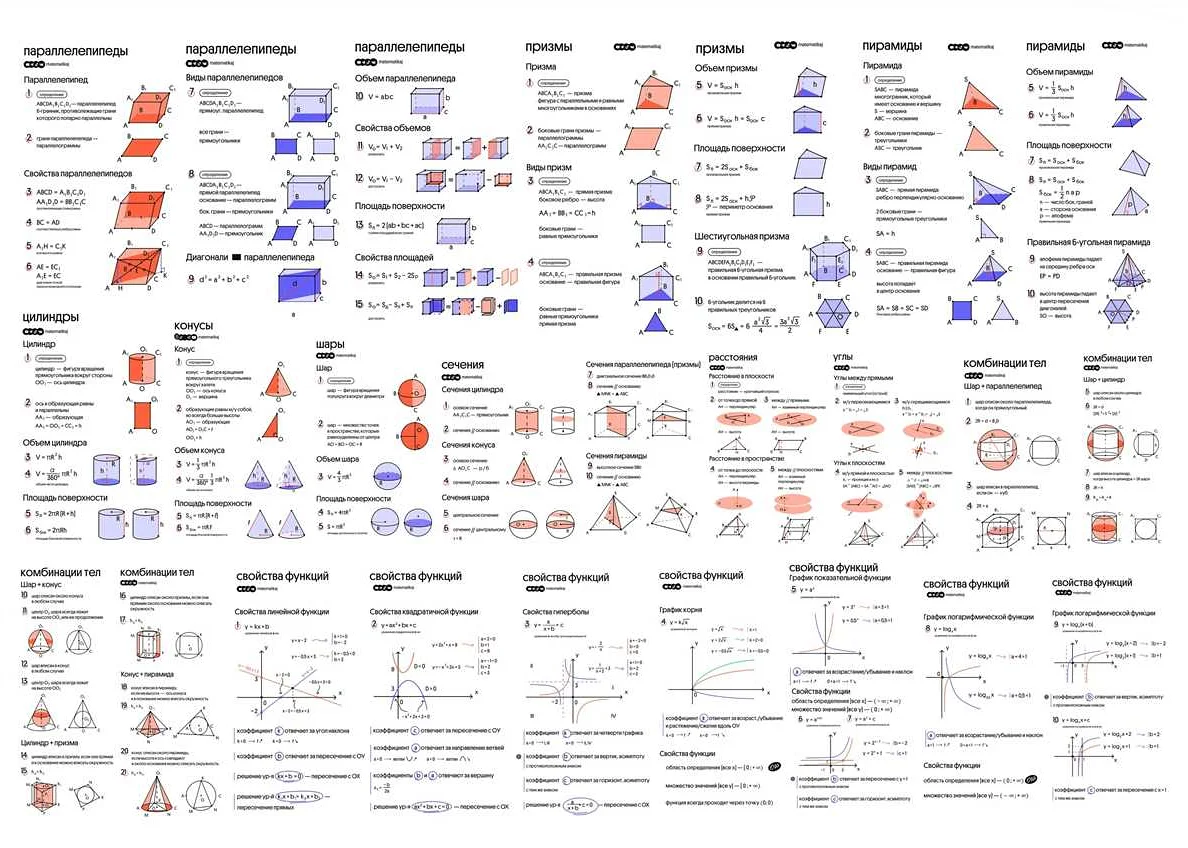
Раздел 3 посвящен изучению формул, необходимых для подготовки к ЕГЭ по математике профильного уровня.
В этом разделе мы рассмотрим следующие формулы:
- Формула квадратного уравнения: x = (-b ± √(b²-4ac))/(2a)
- Формула площади прямоугольника: S = a * b
- Формула площади треугольника: S = (1/2) * a * h
- Формула объема параллелепипеда: V = a * b * h
- Формула длины окружности: L = 2πr
Эти формулы являются основными и широко используются при решении задач на ЕГЭ. Они помогут вам более эффективно подготовиться и успешно справиться с экзаменом.
Рекомендуется практиковаться в применении этих формул на различных задачах, чтобы научиться их использовать и привыкнуть к их применению в разных ситуациях.
Формулы для работы с функциями
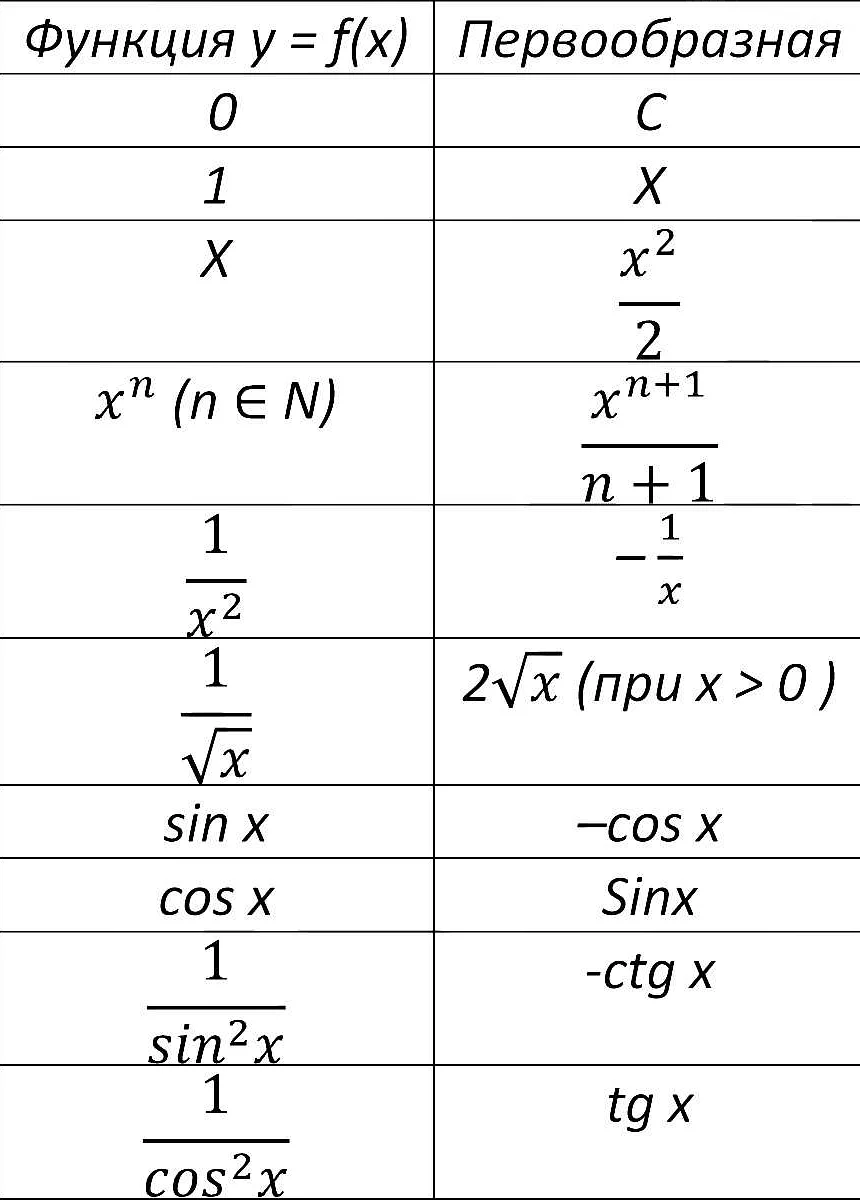
В математике функция представляет собой отображение, которое каждому элементу из одного множества сопоставляет элемент из другого множества. Работа с функциями включает в себя несколько важных формул, которые помогают анализировать и решать задачи.
1. Формула суммы арифметической прогрессии:
| Sn = (a1 + an) * n / 2 |
где Sn — сумма первых n членов арифметической прогрессии, a1 — первый член прогрессии, an — последний член прогрессии, n — количество членов прогрессии.
2. Формула суммы геометрической прогрессии:
| Sn = a * (qn — 1) / (q — 1) |
где Sn — сумма первых n членов геометрической прогрессии, a — первый член прогрессии, q — знаменатель прогрессии, n — количество членов прогрессии.
3. Формула линейной функции:
| y = kx + b |
где y — значение функции, k — коэффициент при x, b — свободный член.
4. Формула параболы:
| y = ax2 + bx + c |
где y — значение функции, a — коэффициент при x2, b — коэффициент при x, c — свободный член.
Эти формулы являются основными для работы с функциями и широко используются при решении задач ЕГЭ по математике профильного уровня.
Раздел 4
В данном разделе представлены основные формулы и свойства, необходимые для подготовки к ЕГЭ по математике профильного уровня.
-
- Формула сокращенного умножения
Для любых чисел a, b и c справедливо равенство:
a^2 — b^2 = (a + b)(a — b)
-
- Формула суммы кубов
Для любого натурального числа n справедливо равенство:
1^3 + 2^3 + … + n^3 = (1 + 2 + … + n)^2
-
- Формула бинома Ньютона
Для любых чисел a и b и натурального числа n справедливо равенство:
(a + b)^n = C(n, 0)a^n*b^0 + C(n, 1)a^(n-1)*b^1 + … + C(n, n-1)a^1*b^(n-1) + C(n, n)a^0*b^n
где C(n, k) — биномиальный коэффициент, равный n!/(k!(n-k)!)
-
- Формула синуса
Для любого треугольника ABC справедливо равенство:
a/sin(A) = b/sin(B) = c/sin(C) = 2R
где a, b, c — стороны треугольника, A, B, C — соответствующие углы, R — радиус описанной окружности
-
- Формула косинуса
Для любого треугольника ABC справедливо равенство:
c^2 = a^2 + b^2 — 2ab*cos(C)
где c — сторона треугольника, a, b — смежные стороны, C — их междуугольный угол
Эти формулы и свойства помогут вам решать различные задачи на экзамене и повысят эффективность вашей подготовки.
Формулы для работы с логарифмами и экспонентами
Вот несколько формул, которые помогут вам работать с логарифмами и экспонентами:
1. Формула для перехода от логарифмической формы записи к экспоненциальной:
a = bx
где a — основание логарифма, b — число, x — логарифм данного числа по основанию a.
2. Формула для перехода от экспоненциальной формы записи к логарифмической:
x = logba
где a — число, b — основание логарифма, x — логарифм данного числа по основанию b.
3. Формула для вычисления натурального логарифма:
ln(x)
где x — число, ln — натуральный логарифм числа x.
4. Формула для вычисления десятичного логарифма:
log(x)
где x — число, log — десятичный логарифм числа x.
5. Формула для вычисления экспоненты:
ex
где x — степень, e — основание экспоненты.
Запомните эти формулы и упражняйтесь в их использовании, чтобы успешно справиться с заданиями по логарифмам и экспонентам на ЕГЭ по математике профильного уровня.
Вопрос-ответ:
Какие формулы необходимо знать для подготовки к ЕГЭ по математике профильного уровня?
Для успешной подготовки к ЕГЭ по математике профильного уровня необходимо знать основные формулы, такие как формулы трехгранника, формулы площади и объема, формулы тригонометрии, формулы для работы с функциями и другие.
Какие формулы трехгранника необходимо знать для подготовки к ЕГЭ по математике профильного уровня?
Для подготовки к ЕГЭ по математике профильного уровня необходимо знать формулы для вычисления объема и площади трехгранника. Например, формула для объема параллелепипеда: V = a * b * h, где a, b и h — длины сторон параллелепипеда.
Какие формулы тригонометрии необходимо знать для подготовки к ЕГЭ по математике профильного уровня?
Для подготовки к ЕГЭ по математике профильного уровня необходимо знать основные формулы тригонометрии, такие как формулы синуса, косинуса и тангенса. Например, формула синуса: sin(A) = a / c, где A — угол, a — противолежащий катет, c — гипотенуза прямоугольного треугольника.
Какие формулы для работы с функциями необходимо знать для подготовки к ЕГЭ по математике профильного уровня?
Для подготовки к ЕГЭ по математике профильного уровня необходимо знать формулы для работы с функциями, такие как формула суммы и разности функций, формула произведения функций, формула частного функций и другие. Например, формула суммы функций: (f + g)(x) = f(x) + g(x), где f(x) и g(x) — функции.
Какие еще формулы необходимо знать для подготовки к ЕГЭ по математике профильного уровня, кроме указанных выше?
Помимо указанных выше формул, для подготовки к ЕГЭ по математике профильного уровня необходимо знать формулы для работы с логарифмами, формулы для работы с производными и интегралами, формулы для решения уравнений и неравенств, а также другие формулы, которые встречаются в программе ЕГЭ.
Какие формулы нужно знать для подготовки к ЕГЭ по математике профильного уровня?
Для подготовки к ЕГЭ по математике профильного уровня нужно знать такие формулы, как формула синуса, формула косинуса, формула площади треугольника по двум сторонам и углу между ними, формула площади круга, формула объема и поверхности шара, формула площади поверхности цилиндра и т.д.
Какие формулы нужно знать для решения задач на геометрию в ЕГЭ по математике профильного уровня?
Для решения задач на геометрию в ЕГЭ по математике профильного уровня нужно знать такие формулы, как формула синуса, формула косинуса, формула площади треугольника по двум сторонам и углу между ними, формула площади круга, формула объема и поверхности шара, формула площади поверхности цилиндра и т.д. Эти формулы помогут вам находить значения неизвестных в задачах, связанных с геометрией.
Раздел 5
В пятом разделе ЕГЭ по математике профильного уровня рассматриваются темы, связанные с функциями и их свойствами. Этот раздел включает в себя такие темы, как:
1. Определение функции и ее свойства.
2. Графики функций и их анализ. В данном разделе необходимо уметь строить графики функций, анализировать их свойства, такие как монотонность, выпуклость, наличие экстремумов и асимптот.
3. Решение уравнений и неравенств с помощью функций. В данном разделе необходимо уметь решать уравнения и неравенства, в которых функции выступают в качестве неизвестных или известных.
4. Производные и их применение. В данном разделе необходимо уметь находить производные функций, анализировать их свойства, находить экстремумы функций с помощью производных.
5. Интегралы и их применение. В данном разделе необходимо уметь находить неопределенные и определенные интегралы, решать задачи на вычисление площадей, длин дуг и объемов, используя интегралы.
Все эти темы требуют хорошего понимания основных понятий и методов работы с функциями. Рекомендуется основательно изучить каждую тему и много практиковаться, чтобы успешно справиться с этим разделом ЕГЭ по математике профильного уровня.



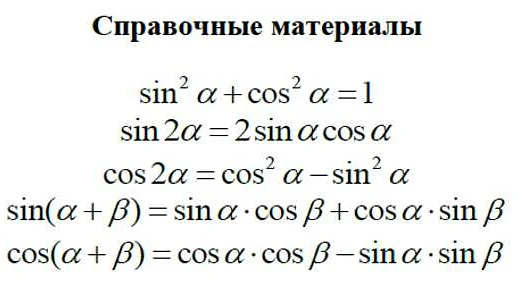
Статья очень полезная и практичная, особенно для тех, кто готовится к ЕГЭ по математике профильного уровня. В ней представлены формулы, которые помогут ученикам систематизировать свои знания и эффективно подготовиться к экзамену. Я сам столкнулся с трудностями в понимании и запоминании этих формул, поэтому такая статья является настоящим находкой для меня. Теперь у меня есть четкий список формул, который я могу изучать и повторять перед экзаменом. Также в статье есть подробные объяснения каждой формулы, что помогает лучше понять их суть и применение. Я очень благодарен автору за такую информацию и буду использовать ее для своей подготовки. Советую всем, кто готовится к ЕГЭ по математике профильного уровня, обратить внимание на эту статью.