Формулы на огэ по математике которых нет в справочном материале

В статье рассматриваются формулы и приёмы решения задач по математике, которых нет в справочном материале для ОГЭ. Узнайте, какие методы помогут вам успешно справиться с экзаменом и повысить свои шансы на получение высокого балла.

Ежегодно тысячи выпускников стараются успешно сдать Основной государственный экзамен по математике. Подготовка к этому экзамену требует не только изучения основных формул и теорем, но и знания более сложных формул, которых нет в справочном материале.

Какие именно формулы стоит знать, чтобы повысить свои шансы на успешное сдачу ОГЭ по математике? В этой статье мы рассмотрим несколько таких формул, которые могут оказаться полезными на экзамене.

Формула Бинома Ньютона: данная формула позволяет раскрывать скобки в выражениях типа (а + b)^n, где n — натуральное число.

Пример использования: (а + b)^2 = а^2 + 2аб + b^2

Формула суммы углов в многоугольнике: сумма внутренних углов n-угольника равна (n-2) * 180°.

Пример использования: сумма внутренних углов треугольника равна (3-2) * 180° = 180°.

Знание данных формул поможет вам решать более сложные задачи на экзамене и повысит ваши шансы на успешную сдачу ОГЭ по математике. Помимо этих формул, важно также уделить внимание решению типовых задач, тренировке навыков анализа и логического мышления.

Раздел 1: Свойства прямых и плоскостей

В данном разделе мы рассмотрим основные свойства прямых и плоскостей, которые важны для успешной подготовки к ОГЭ по математике.

1. Уравнение прямой на плоскости имеет вид y = kx + b, где k — коэффициент наклона, а b — свободный член. Коэффициент наклона определяет угол наклона прямой относительно оси x.

2. Прямые, параллельные оси y или x, имеют бесконечный коэффициент наклона (k=±∞).

3. Угол между прямыми на плоскости можно найти с помощью формулы: tan α = (k1 — k2) / (1 + k1 * k2), где α — искомый угол, k1 и k2 — коэффициенты наклона прямых.

4. Параллельные прямые имеют одинаковый коэффициент наклона.

5. Прямые, перпендикулярные друг другу, имеют коэффициенты наклона, удовлетворяющие условию k1 * k2 = -1.

6. Уравнение плоскости в пространстве имеет вид Ax + By + Cz + D = 0, где A, B и C — коэффициенты плоскости, а D — свободный член.

7. Плоскости, параллельные одной и той же прямой, имеют одинаковые коэффициенты A, B и C.

8. Плоскости, перпендикулярные друг другу, имеют коэффициенты A1 * A2 + B1 * B2 + C1 * C2 = 0.

9. Угол между плоскостями можно найти с помощью формулы: cos α = ((A1 * A2 + B1 * B2 + C1 * C2) / (sqrt(A1^2 + B1^2 + C1^2) * sqrt(A2^2 + B2^2 + C2^2)), где α — искомый угол, A1, B1, C1 и A2, B2, C2 — коэффициенты плоскостей.

Видео по теме:

Раздел 2: Арифметические операции с корнями и степенями

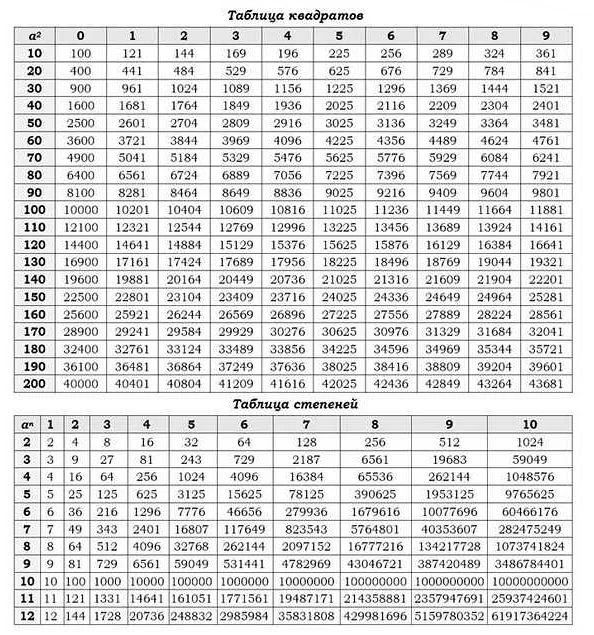
В этом разделе мы рассмотрим основные арифметические операции с корнями и степенями, которые могут встретиться на экзамене по математике ОГЭ.

Для начала вспомним основные правила упрощения выражений с корнями:

• Корень из произведения равен произведению корней: √(a * b) = √a * √b
• Корень из частного равен частному корней: √(a / b) = √a / √b
• Корень из степени равен степени корня: √(a^b) = (a^(1/b))
• Корень из корня равен корню из произведения: √(√a) = √(a^(1/2)) = a^(1/4)

Также не забываем про правила возведения в степень:

• Число, возведенное в 0-ю степень, равно 1: a^0 = 1
• Число, возведенное в положительную степень, равно произведению этого числа самого на себя столько раз, сколько указано в степени: a^n = a * a * … * a (n раз)
• Число, возведенное в отрицательную степень, равно обратному числу, возведенному в положительную степень: a^(-n) = 1/(a^n)

Знание этих простых правил поможет вам эффективно выполнять арифметические операции с корнями и степенями на экзамене по математике ОГЭ.

Раздел 3: Решение систем уравнений с помощью матриц и детерминантов

В этом разделе мы рассмотрим методы решения систем уравнений с помощью матриц и детерминантов. Эти методы позволяют эффективно находить решения систем уравнений и решать задачи, связанные с ними.

Для начала введем понятие матрицы. Матрицей размера m × n называется прямоугольная таблица из m строк и n столбцов, элементы которой обозначаются aij, где i — номер строки, j — номер столбца. Матрицы могут быть использованы для представления системы уравнений в компактной форме.

Рассмотрим линейную систему уравнений:

a11x1 + a12x2 + … + a1nxn = b1

a21x1 + a22x2 + … + a2nxn = b2

……………………………….

am1x1 + am2x2 + … + amnxn = bm

где aij, bi — коэффициенты, xi — неизвестные, m — количество уравнений, n — количество неизвестных. Матричная форма этой системы имеет вид:

A · X = B

где A — матрица коэффициентов, X — вектор неизвестных, B — вектор свободных членов.

Для решения системы уравнений с помощью матрицы A необходимо найти обратную матрицу A-1. Обратная матрица существует только для квадратных матриц (т.е. матриц, у которых количество строк и столбцов одинаково).

Для нахождения обратной матрицы A-1 используется формула:

A-1 = (1 / det(A)) · adj(A)

где det(A) — определитель матрицы A, adj(A) — матрица алгебраических дополнений матрицы A.

Определитель матрицы можно найти с помощью разложения по любой строке или столбцу. Для матрицы размера 2 × 2 определитель вычисляется по формуле:

det(A) = a 11 · a 22 — a 12 · a 21

Для матрицы размера больше 2 × 2 определитель можно вычислить с помощью разложения по первой строке или первому столбцу. Разложение определителя происходит по формуле:

det(A) = a11 · A11 — a12 · A12 + a13 · A13 — … + (-1)1 + n · a1n · A1n

где Aij — минор элемента aij, который определяется вычеркиванием i-й строки и j-го столбца из матрицы A.

Зная обратную матрицу A-1 и вектор свободных членов B, можно найти вектор неизвестных X по формуле:

X = A-1 · B

Таким образом, решение системы уравнений сводится к нахождению обратной матрицы и умножению ее на вектор свободных членов.

Теперь мы знаем, как решать системы уравнений с помощью матриц и детерминантов. Эти методы могут быть полезными при подготовке к ОГЭ по математике, так как позволяют эффективно находить решения систем уравнений и решать задачи, связанные с ними.

Раздел 4: Тригонометрические тождества и формулы

Тригонометрические тождества

1. Формула сложения для синусов: sin(A + B) = sin(A) * cos(B) + cos(A) * sin(B)

2. Формула сложения для косинусов: cos(A + B) = cos(A) * cos(B) — sin(A) * sin(B)

3. Формула удвоения для синуса: sin(2A) = 2 * sin(A) * cos(A)

4. Формула удвоения для косинуса: cos(2A) = cos^2(A) — sin^2(A)

5. Формула разности для синусов: sin(A — B) = sin(A) * cos(B) — cos(A) * sin(B)

6. Формула разности для косинусов: cos(A — B) = cos(A) * cos(B) + sin(A) * sin(B)

7. Формула половинного угла для синуса: sin(A/2) = sqrt((1 — cos(A))/2)

8. Формула половинного угла для косинуса: cos(A/2) = sqrt((1 + cos(A))/2)

Тригонометрические формулы

1. Формула сокращенного умножения для синуса: 2 * sin(A) * sin(B) = cos(A — B) — cos(A + B)

2. Формула сокращенного умножения для косинуса: 2 * cos(A) * cos(B) = cos(A — B) + cos(A + B)

3. Формула сокращенного умножения для тангенса: 2 * tan(A) * tan(B) = 1 — tan^2(A + B)

4. Формула суммы квадратов синуса и косинуса: sin^2(A) + cos^2(A) = 1

5. Формула суммы косинусов: cos(A) + cos(B) = 2 * cos((A + B)/2) * cos((A — B)/2)

6. Формула разности косинусов: cos(A) — cos(B) = -2 * sin((A + B)/2) * sin((A — B)/2)

7. Формула суммы синусов: sin(A) + sin(B) = 2 * sin((A + B)/2) * cos((A — B)/2)

8. Формула разности синусов: sin(A) — sin(B) = 2 * cos((A + B)/2) * sin((A — B)/2)

Раздел 5: Построение графиков функций и нахождение их свойств

Для построения графика функции необходимо:

1. Найти область определения функции.
2. Найти особые точки функции (точки разрыва, точки разреза).
3. Найти значения функции для выбранных значений аргумента.
4. Построить график функции на координатной плоскости.

При построении графика функции необходимо учитывать следующие свойства:

• Симметричность графика функции относительно оси абсцисс (график функции f(x) симметричен относительно оси OX, если f(x) = f(-x) для всех x из области определения функции).
• Периодичность графика функции (график функции f(x) является периодическим с периодом T, если f(x + T) = f(x) для всех x из области определения функции).
• Монотонность графика функции (график функции f(x) является возрастающим на интервале I, если для любых x1 и x2 из I, где x1 < x2, выполняется неравенство f(x1) ≤ f(x2)).
• Нули функции (значения аргумента, при которых функция равна нулю).
• Экстремумы функции (максимумы и минимумы функции).

Знание этих свойств позволит эффективно строить графики функций и находить их основные характеристики.

ФункцияОбласть определенияОсобые точкиСимметрияПериодичностьМонотонностьНули функцииЭкстремумы

f(x) = x^2	любое действительное число	нет	относительно оси OY	нет	возрастает на (-∞, 0) и (0, +∞)	0	минимум в точке (0, 0)
f(x) = sin(x)	любое действительное число	нет	относительно оси OY	2π	нет	0	максимумы в точках (π/2, 1) и (3π/2, 1); минимумы в точках (π, -1) и (2π, -1)

Раздел 6: Использование комбинаторики в задачах на вероятность

Одним из основных понятий комбинаторики является понятие перестановки. Перестановкой называется упорядоченная выборка элементов из множества. Например, если из множества {a, b, c} выбираются все возможные упорядоченные тройки, то получится 6 перестановок: (a, b, c), (a, c, b), (b, a, c), (b, c, a), (c, a, b), (c, b, a).

Для решения задач на вероятность, в которых используется комбинаторика, необходимо знать формулу для вычисления числа перестановок. Формула для вычисления числа перестановок из n элементов равна n! (n факториал). Факториал числа n обозначается символом ! и равен произведению всех чисел от 1 до n. Например, 4! = 4 * 3 * 2 * 1 = 24.

Комбинаторика также используется при решении задач на сочетания. Сочетаниями называются неупорядоченные выборки элементов из множества. Например, если из множества {a, b, c} выбираются все возможные неупорядоченные пары, то получится 3 сочетания: (a, b), (a, c), (b, c).

Для вычисления числа сочетаний из n элементов по k элементов используется формула: С(n, k) = n! / (k! * (n — k)!), где С(n, k) — число сочетаний из n элементов по k элементов.

При решении задач на вероятность с использованием комбинаторики, необходимо учитывать, что вероятность события равна отношению числа благоприятных исходов к общему числу исходов. Также необходимо уметь применять комбинаторные формулы для вычисления числа благоприятных исходов.

Название формулыФормулаПример

Факториал	n! = n * (n-1) * … * 2 * 1	4! = 4 * 3 * 2 * 1 = 24
Число перестановок	P(n) = n!	P(4) = 4! = 24
Число сочетаний	C(n, k) = n! / (k! * (n — k)!)	C(5, 2) = 5! / (2! * (5 — 2)!) = 10

Раздел 7: Вычисление периметра и площади фигур нестандартной формы

Для вычисления периметра фигур нестандартной формы необходимо сложить длины всех сторон фигуры. Если фигура имеет кривые стороны, можно разделить ее на более простые геометрические фигуры (такие как прямоугольники, треугольники) и сложить их периметры.

Вычисление площади фигур нестандартной формы может быть более сложным. Однако, если фигура может быть разделена на простые геометрические фигуры (такие как прямоугольники, треугольники), можно вычислить площади каждой из них и сложить полученные значения. В случае криволинейных фигур необходимо использовать особые методы вычисления площади, например, метод механического интегрирования.

Важно помнить, что для вычисления периметра и площади фигур необходимо знать значения соответствующих сторон и углов. Поэтому перед вычислениями необходимо изучить характеристики фигуры и провести все необходимые измерения.

При решении задач по вычислению периметра и площади фигур нестандартной формы следует использовать формулы, изученные в предыдущих разделах. Также помните о необходимости проверки правильности результата и округления ответа до необходимой точности.

Раздел 8: Основные свойства пропорциональности

Пропорциональность между двумя величинами можно записать следующим образом: если две величины $a$ и $b$ пропорциональны, то их отношение всегда равно постоянной величине $k$. Это можно записать уравнением:

$$\frac{a}{b} = k$$

Также можно записать пропорциональность через знак пропорциональности «$\propto$». Тогда уравнение будет выглядеть так:

$$a \propto b$$

Пропорциональность между тремя величинами можно записать следующим образом: если три величины $a$, $b$ и $c$ пропорциональны, то их отношение всегда равно постоянной величине $k$. Это можно записать уравнением:

$$\frac{a}{b} = \frac{b}{c} = k$$

Свойства пропорциональности:

1. Если две величины пропорциональны, то их отношение всегда равно постоянной величине.

2. При умножении или делении всех величин в пропорции на одну и ту же ненулевую величину, пропорция остается пропорциональной.

3. При суммировании или вычитании пропорциональных величин получается новая пропорциональная величина.

Вопрос-ответ:

Какие формулы ОГЭ по математике отсутствуют в справочном материале?

В справочном материале ОГЭ по математике отсутствуют формулы по теме «Статистика». Там нет формул для вычисления выборочного среднего, выборочной дисперсии и выборочной среднеквадратической ошибки. Но эти формулы очень важны для выполнения задач на данную тему.

Как подготовиться к ОГЭ по математике, если в справочном материале отсутствуют некоторые формулы?

Если в справочном материале ОГЭ по математике отсутствуют некоторые формулы, вам придется запоминать их самостоятельно. Рекомендуется составить список всех формул, которые отсутствуют в справочном материале, и регулярно повторять их, чтобы закрепить в памяти.

Какие формулы по теме «Статистика» нужно знать для ОГЭ по математике?

Для выполнения задач по теме «Статистика» на ОГЭ по математике необходимо знать формулы для вычисления выборочного среднего, выборочной дисперсии и выборочной среднеквадратической ошибки. Выборочное среднее вычисляется по формуле: Xср = (x1 + x2 + … + xn) / n, где Xср — выборочное среднее, x1, x2, …, xn — значения в выборке, n — количество значений в выборке. Выборочная дисперсия вычисляется по формуле: Dср = ((x1 — Xср)^2 + (x2 — Xср)^2 + … + (xn — Xср)^2) / (n — 1), где Dср — выборочная дисперсия. Выборочная среднеквадратическая ошибка вычисляется по формуле: σср = sqrt(Dср/n), где σср — выборочная среднеквадратическая ошибка.

Какие есть способы запоминания формул, которых нет в справочном материале?

Есть несколько способов запоминания формул, которых нет в справочном материале. Один из них — составить мнемонические предложения, в которых первые буквы слов образуют формулу. Например, для формулы вычисления выборочного среднего можно использовать предложение «Хороший художник Знакомит с новыми нотками». Другой способ — регулярное повторение формул и их применение в практических задачах. Это поможет закрепить формулы в памяти и улучшить понимание их сути.