Прикладная математика где используется

Прикладная математика — это наука, которая находит применение во многих областях жизни. Она используется в финансах, экономике, технике, компьютерных науках, медицине и других сферах. От оптимизации бизнес-процессов до прогнозирования погоды — прикладная математика играет важную роль в решении реальных проблем и создании новых технологий. Используя математические методы и модели, специалисты могут анализировать данные, прогнозировать тренды и принимать обоснованные решения. Прикладная математика — это мощный инструмент, который помогает нам лучше понимать и улучшать мир вокруг нас.

Прикладная математика — это наука, которая применяет математические методы для решения реальных проблем. Она находит свое применение во множестве областей, от экономики и финансов до медицины и инженерии. Математические модели и методы, разработанные в рамках прикладной математики, играют важную роль в прогнозировании, оптимизации и принятии решений.

Одной из областей, где прикладная математика находит широкое применение, является физика. Она помогает в исследовании и моделировании физических процессов, таких как движение частиц и взаимодействие полей. Математические методы позволяют предсказывать поведение системы и проверять теоретические гипотезы.

Еще одной важной областью применения прикладной математики является информационная технология. Математические алгоритмы используются для решения задач обработки данных, компьютерного зрения, машинного обучения и цифровой обработки сигналов. Они обеспечивают эффективность и точность работы компьютерных систем и программ.

Например, алгоритмы компьютерного зрения, основанные на методах обработки изображений и статистического анализа, применяются для распознавания лиц, определения объектов на изображениях и автоматического анализа видео.

Прикладная математика также играет важную роль в финансовой аналитике и экономическом моделировании. Математические методы позволяют оценивать риски и доходность инвестиций, моделировать финансовые процессы и прогнозировать развитие экономики. Они помогают принимать обоснованные решения на основе данных и анализа рынка.

Таким образом, прикладная математика находит свое применение во множестве областей и играет ключевую роль в развитии науки и технологий. Ее методы и модели позволяют решать сложные задачи и прогнозировать поведение систем. Без прикладной математики было бы значительно сложнее развивать и оптимизировать современные технологии и процессы.

Финансовая сфера

Прикладная математика широко применяется в финансовой сфере для анализа и прогнозирования финансовых рынков, определения рисков и разработки оптимальных стратегий инвестирования.

Одной из важных областей применения математических методов в финансах является портфельное управление. Задача портфельного управления заключается в оптимизации структуры инвестиционного портфеля с целью получения максимальной доходности при заданных уровнях риска. Математические модели позволяют оценить эффективность различных инвестиционных стратегий и выбрать наиболее оптимальную.

Другим примером применения математики в финансах является анализ временных рядов. Временные ряды представляют собой последовательность данных, изменяющихся во времени. Используя математические методы, можно предсказать будущие значения временного ряда, что позволяет принимать решения о покупке или продаже ценных бумаг на финансовом рынке.

Также математические методы применяются для моделирования финансовых инструментов, таких как опционы или фьючерсы. Моделирование позволяет оценить стоимость и риски данных инструментов, а также разработать стратегии их использования.

Примеры применения прикладной математики в финансовой сфере:

Разработка математических моделей для определения оптимального портфеля инвестиций.

Анализ временных рядов для прогнозирования изменений на финансовых рынках.

Моделирование финансовых инструментов для оценки и управления рисками.

Видео по теме:

Транспортное строительство

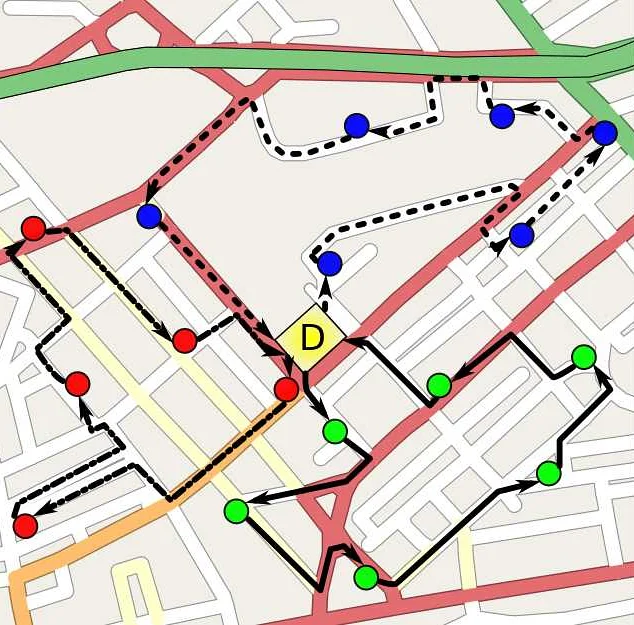
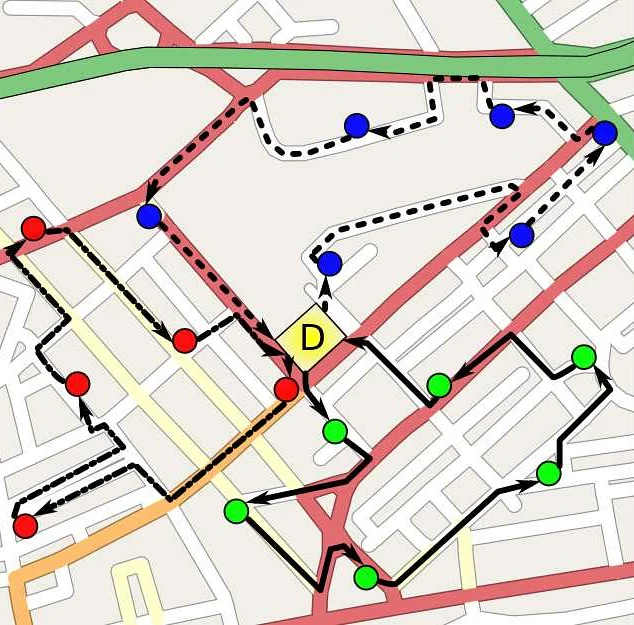
Прикладная математика играет важную роль в транспортном строительстве, обеспечивая оптимальное планирование и управление инфраструктурными проектами. Математические модели позволяют анализировать и прогнозировать различные аспекты транспортной системы, такие как пропускная способность, эффективность движения, загруженность и безопасность.

Одним из примеров применения прикладной математики в транспортном строительстве является оптимизация планирования дорожных сетей. Математические модели позволяют определить наиболее эффективные маршруты, учитывая различные параметры, такие как расстояние, время пути, стоимость и экологические факторы.

Еще одним примером является применение математических методов для оптимизации расписания общественного транспорта. С помощью математических моделей можно оптимально распределить ресурсы и определить оптимальное время прибытия и отправления транспортных средств, чтобы минимизировать время ожидания пассажиров и снизить заторы.

Также прикладная математика широко используется для анализа и прогнозирования потоков транспортных средств. Математические модели позволяют предсказывать объемы движения на различных участках дороги и оптимизировать систему управления трафиком, чтобы снизить заторы и улучшить безопасность на дорогах.

Примеры применения прикладной математики в транспортном строительстве:

Оптимизация планирования дорожных сетей

Оптимизация расписания общественного транспорта

Анализ и прогнозирование потоков транспортных средств

Медицина и фармацевтика

Прикладная математика играет важную роль в медицине и фармацевтике, обеспечивая разработку и оптимизацию различных процедур, лекарственных препаратов и медицинских устройств.

Одним из примеров применения прикладной математики в медицине является моделирование и симуляция физиологических процессов в организме человека. С помощью математических моделей ученые и врачи могут изучать и предсказывать различные биологические процессы, такие как кровообращение, дыхание, работа органов и тканей. Это позволяет оптимизировать лечение пациентов, планировать операции и проводить исследования новых методов диагностики и лечения.

Также прикладная математика используется для анализа и обработки медицинских данных. Большие объемы данных, получаемые врачами и исследователями, требуют эффективных алгоритмов и методов для их анализа и интерпретации. Математические модели и статистические методы помогают выявлять закономерности, определять риски и прогнозировать результаты лечения.

В фармацевтике прикладная математика применяется для разработки новых лекарственных препаратов, оптимизации их дозировки и расчета эффективности. Математические модели позволяют ученым изучать взаимодействие препаратов с организмом, анализировать их фармакокинетику и фармакодинамику. Это помогает создавать более безопасные и эффективные лекарства.

Таким образом, прикладная математика играет важную роль в медицине и фармацевтике, обеспечивая разработку новых методов диагностики и лечения, оптимизацию процедур и лекарственных препаратов, анализ и интерпретацию медицинских данных.

Вопрос-ответ:

Для чего нужна прикладная математика?

Прикладная математика используется для решения практических задач в различных областях, таких как физика, экономика, биология и т.д. Она помогает анализировать данные, моделировать системы, оптимизировать процессы и предсказывать результаты.

Какие области применения прикладной математики?

Прикладная математика применяется во многих областях, например в физике, экономике, биологии, медицине, компьютерной науке и т.д. Она используется для моделирования физических процессов, прогнозирования рыночных тенденций, анализа генетических данных и многое другое.

Какие задачи решает прикладная математика?

Прикладная математика решает разнообразные задачи, такие как оптимизация, прогнозирование, моделирование, анализ данных и т.д. Например, с ее помощью можно оптимизировать рабочие процессы в производстве, прогнозировать погоду, моделировать поведение финансовых рынков и анализировать медицинские данные.

Какие примеры применения прикладной математики в биологии?

Прикладная математика играет важную роль в биологии. Она используется для моделирования генетических процессов, анализа эволюционных траекторий, предсказания распространения инфекционных заболеваний и многое другое. Например, с ее помощью можно разрабатывать математические модели популяций животных или исследовать механизмы действия лекарственных препаратов.

Где применяется прикладная математика в компьютерной науке?

Прикладная математика имеет широкое применение в компьютерной науке. Она используется для разработки алгоритмов и структур данных, оптимизации программного кода, анализа сложности алгоритмов и многое другое. Например, с ее помощью можно разрабатывать алгоритмы машинного обучения, оптимизировать работу баз данных или анализировать сетевые структуры.

Зачем нужна прикладная математика?

Прикладная математика нужна для решения реальных проблем и задач, которые возникают в различных областях науки, техники и экономики. Она позволяет проводить анализ данных, моделировать процессы и принимать взвешенные решения на основе математических моделей и методов.

Какие области применения прикладной математики существуют?

Прикладная математика применяется во многих областях, включая физику, химию, биологию, медицину, экономику, финансы, технику, компьютерные науки и т.д. Она используется для моделирования физических и биологических процессов, оптимизации систем, анализа данных, прогнозирования и многих других целей.

Энергетика и экология

Прикладная математика имеет широкое применение в области энергетики и экологии, где её использование позволяет решать множество сложных задач.

Одной из областей, где применяется прикладная математика, является оптимизация процессов производства энергии. Математические модели позволяют оптимизировать работу энергетических систем, учитывая различные ограничения и требования к производству энергии.

Еще одним примером применения прикладной математики в энергетике является моделирование и прогнозирование энергетических систем. Математические модели позволяют анализировать и прогнозировать эффективность и работу энергетических систем для оптимального использования ресурсов и улучшения экологической обстановки.

В области экологии прикладная математика применяется для оценки и моделирования различных аспектов окружающей среды. Например, математические модели могут использоваться для анализа загрязнения воздуха, воды и почвы, оценки воздействия промышленных объектов на окружающую среду, и определения наилучших стратегий управления экологическими ресурсами.

Таким образом, прикладная математика играет важную роль в энергетике и экологии, позволяя разрабатывать эффективные и устойчивые решения для решения сложных проблем в этих областях.

Телекоммуникации и информационные технологии

Прикладная математика играет важную роль в сфере телекоммуникаций и информационных технологий. Эта область применения включает разные аспекты, начиная от разработки и оптимизации сетей связи до разработки алгоритмов обработки сигналов и компьютерного зрения.

Примеры применения прикладной математики в телекоммуникациях и информационных технологиях:

1. Оптимизация сетей связи: математические модели используются для оптимизации распределения ресурсов, маршрутизации трафика и управления сетевыми протоколами.
2. Кодирование и сжатие данных: математические методы применяются для разработки эффективных алгоритмов сжатия и кодирования данных, что позволяет увеличить пропускную способность и снизить объем передаваемой информации.
3. Обработка сигналов: математические методы применяются для фильтрации и обработки сигналов, что позволяет улучшить качество передачи звука и изображений.
4. Криптография и безопасность: математические алгоритмы используются для защиты информации и шифрования данных в системах связи и информационных технологиях.
5. Анализ данных и машинное обучение: прикладная математика применяется для разработки алгоритмов анализа данных, предсказания и классификации, что позволяет извлекать ценные знания из больших объемов информации.

Таким образом, прикладная математика играет важную роль в различных аспектах телекоммуникаций и информационных технологий, способствуя развитию и оптимизации современных коммуникационных систем и технологий.

Производство и логистика

Прикладная математика широко применяется в области производства и логистики для оптимизации различных процессов и решения сложных задач.

Одной из основных задач, решаемых с помощью математических моделей, является оптимальное планирование производственных процессов. Математический аппарат позволяет учесть множество факторов и условий, таких как ограниченные ресурсы, сроки выполнения заказов, производственные мощности и многие другие. Производственные задачи могут быть сформулированы как задачи линейного программирования, дискретной оптимизации или динамического программирования.

В логистике математические модели широко используются для оптимизации маршрутов доставки, планирования складских запасов и управления цепями поставок. Например, задача коммивояжера, которая состоит в нахождении кратчайшего пути, проходящего через все заданные города, может быть использована для оптимизации маршрутов доставки грузов.

Также прикладная математика помогает решать сложные задачи оптимального планирования производства и логистики в реальном времени. Например, с помощью математических моделей возможно оптимизировать распределение задач и ресурсов между рабочими, учитывая их навыки и время выполнения задач.

Таким образом, применение прикладной математики в производстве и логистике позволяет значительно повысить эффективность и экономическую эффективность этих областей, а также сократить затраты на ресурсы и время выполнения задач.

Наука и исследования

Прикладная математика играет важную роль в науке и исследованиях, помогая ученым решать сложные проблемы и разрабатывать новые теории. Она используется во многих областях науки, таких как физика, химия, биология и экология.

В физике прикладная математика используется для моделирования и предсказания физических процессов. Например, она может помочь ученым понять поведение частиц в физических системах или разработать математические модели для описания законов физики. В химии прикладная математика может быть использована для анализа химических реакций и предсказания свойств различных веществ.

В биологии прикладная математика играет роль в изучении генетических особенностей организмов, моделирования популяционных динамик и анализа биологических данных. Она помогает ученым понять принципы эволюции, развития и функционирования живых организмов.

В экологии прикладная математика используется для моделирования экологических систем, анализа данных о распределении видов в природе и прогнозирования эффектов изменения климата на экосистемы. Она помогает ученым понять взаимодействия между различными видами и предсказать последствия различных действий на окружающую среду.

Все эти примеры показывают, что прикладная математика является неотъемлемой частью научных исследований и позволяет ученым получать новые знания и делать открытия.

Спорт и фитнес

Прикладная математика имеет широкое применение в области спорта и фитнеса. Математические модели и методы помогают тренерам и спортсменам анализировать данные, прогнозировать результаты и оптимизировать тренировочные программы.

• Анализ движений: Математическое моделирование позволяет анализировать движения спортсменов и исследовать их биомеханику. Например, математические модели могут использоваться для изучения траектории мяча в футболе или теннисе, оптимизации движений в гимнастике или разработки биомеханических протезов для людей с ограниченными возможностями.
• Оптимизация тренировок: Математические методы могут быть использованы для оптимизации тренировочных программ и планирования расписания тренировок. Например, методы линейного программирования могут помочь распределить тренировочную нагрузку между разными видами тренировок или спортсменами для достижения максимальных результатов.
• Анализ данных: В спорте и фитнесе часто используется анализ данных для определения общей физической формы спортсмена, оценки эффективности тренировок и прогнозирования результатов. Математические методы, такие как регрессионный анализ или анализ временных рядов, могут помочь выявить закономерности и тренды в данных и сделать предсказания.
• Оптимизация стратегий: В таких командных видах спорта, как футбол или баскетбол, математические модели могут помочь тренерам принимать решения и оптимизировать стратегии игры. Например, модели оптимального выбора расстановки игроков на поле или оптимизации передачи мяча могут помочь команде достичь лучших результатов.

Таким образом, прикладная математика играет важную роль в области спорта и фитнеса, помогая тренерам и спортсменам улучшать результаты, оптимизировать тренировки и принимать обоснованные решения.