Порядок действий в математике кто придумал

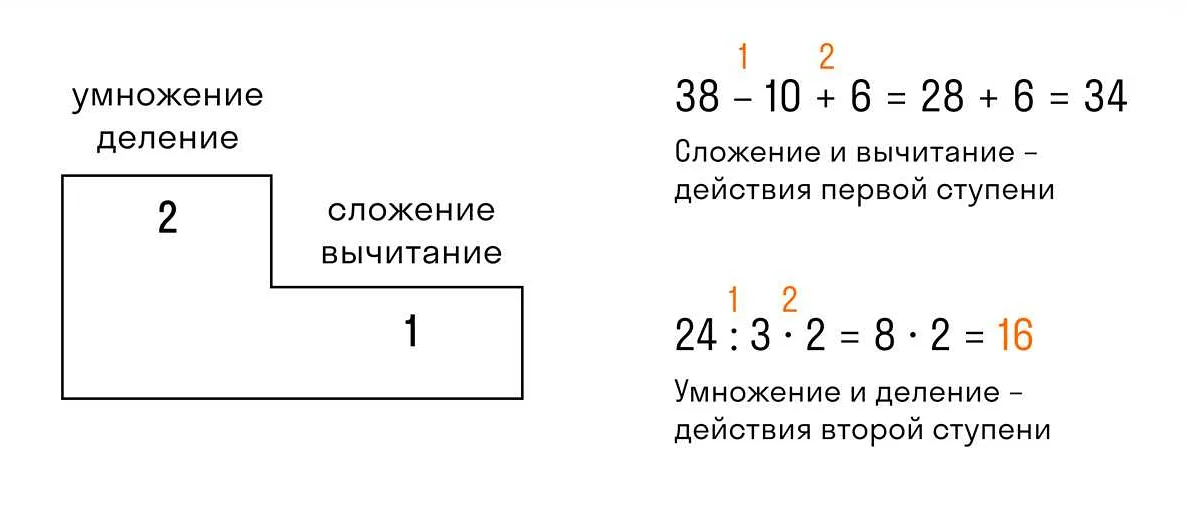
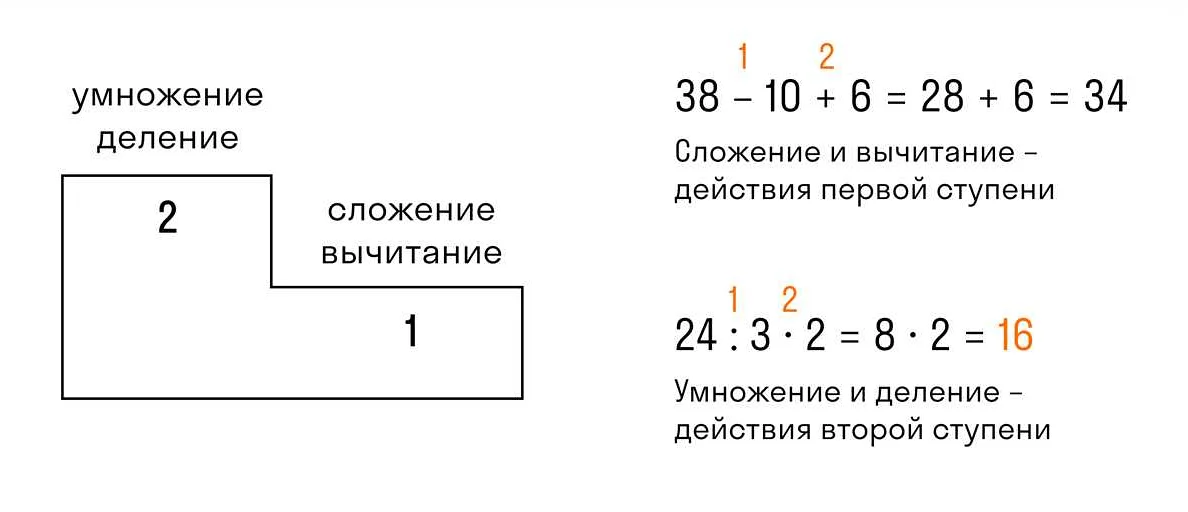
Порядок действий в математике – это система правил, которые определяют последовательность выполнения операций. Изначально этот порядок был разработан и устанавливался математиками в течение многих веков. Мета-описание рассказывает о происхождении и важности правильного порядка действий в математике.

Математика считается одной из старейших наук, ее история насчитывает тысячелетия. Но кто и когда придумал порядок действий, который мы используем по сей день?

Первые шаги в развитии математики были сделаны еще в Древнем Египте и Месопотамии. Здесь люди начали заниматься счетом и разработали систему записи чисел. Однако, их математика была основана на конкретных задачах и не имела абстрактных понятий.

Первые шаги в сторону абстрактной математики были сделаны в Древней Греции. Одним из главных вкладов была разработка алгебры и геометрии. Арифметика, включая порядок действий, также была разработана в Греции. Греки использовали специальные символы для обозначения арифметических операций, таких как сложение и умножение.

Однако, формальный порядок действий, который мы используем сейчас, был придуман в Средние века арабскими математиками. Они впервые использовали знаки «+», «-«, «×» и «÷» и предложили порядок действий, в котором умножение и деление выполняются перед сложением и вычитанием. Эта система была впервые описана арабским математиком Аль-Хорезми в его книге «Китаб аль-мукабала». Этот порядок действий был принят и использовался в Европе и стал стандартом натуральной математики.

Рождение математики: первые шаги к открытию порядка действий

Первые шаги в открытии порядка действий были сделаны еще в древнем мире. Древние месопотамские, египетские и индийские математики использовали особые методы для выполнения арифметических операций. Например, древние египтяне использовали метод, который назывался «методом фракций», для сложения и вычитания чисел. Они представляли числа в виде дробей и использовали таблицы для выполнения вычислений. Также в Индии были разработаны особые символы и правила для выполнения арифметических операций.

Однако, истинное «рождение» математики произошло в Древней Греции. Греческие математики, такие как Пифагор, Евклид и Архимед, внесли огромный вклад в развитие математики, включая открытие и формализацию порядка действий.

Одним из наиболее известных греческих математиков был Евклид, который в своей знаменитой книге «Начала» впервые описал и аксиоматизировал арифметику. Его работа сформировала основу для современной математической логики и алгебры. Также, Греция внесла вклад в развитие геометрии, которая также является важной составляющей математики.

С течением времени, математика продолжила развиваться и расширяться. С появлением арабской числовой системы и использованием десятичной записи чисел, арифметические операции стали более удобными и эффективными.

Сегодня, благодаря развитию математики, мы имеем широкий спектр математических методов и инструментов, которые используются во многих областях науки, техники и экономики. Арифметика, включая порядок действий, стала основой для выполнения сложных вычислений и решения реальных проблем.

ПериодМатематикиВклад

Древний мир	Месопотамские, египетские, индийские математики	Разработка методов выполнения арифметических операций
Древняя Греция	Пифагор, Евклид, Архимед	Открытие и формализация порядка действий
Средние века	Арабские математики	Введение арабской числовой системы и использование десятичной записи чисел

В заключение, история развития математики свидетельствует о том, что порядок действий в арифметике не всегда был известен. Изначально, древние цивилизации использовали различные методы для выполнения арифметических операций. Однако, благодаря работе греческих математиков, особенно Евклида, арифметика получила строгую формализацию и стала фундаментом для развития математики в целом.

Видео по теме:

Математика в Древнем Египте: открытие тайн чисел и операций

Математика в Древнем Египте играла важную роль и использовалась в различных сферах жизни, таких как архитектура, земледелие и торговля. Египтяне разработали свою систему записи чисел, которая называлась египетской десятичной системой. В этой системе использовались только десятичные степени числа 10.

Египтяне использовали специальные символы для записи чисел. Например, символы для чисел 1, 10, 100 и 1000 были изображены в виде линий, а символ для числа 10000 выглядел как лотосовый цветок. Эта система позволяла записывать и выполнять арифметические операции с числами.

Одним из важных достижений древнеегипетской математики было открытие тайны простых чисел. Египтяне знали, что некоторые числа могут быть разложены только на определенные простые множители, и они использовали эту информацию при решении задач.

Египтяне также практиковали сложение, вычитание, умножение и деление. Они использовали специальные методы для выполнения этих операций. Например, для сложения чисел они использовали метод, который назывался «методом счета палочками». Они считали палочки, которые представляли числа, и складывали их вместе.

Древнеегипетская математика была важным элементом египетской культуры и играла важную роль в различных аспектах жизни. Египтяне сделали значительные открытия в области чисел и операций, которые позже были использованы и развиты другими цивилизациями.

Греческая математика: Архимед и развитие алгебры

Греческая математика имела значительное влияние на развитие математики в целом. Один из величайших греческих математиков, Архимед, сыграл ключевую роль в развитии алгебры.

Архимед, живший в III веке до н.э., был известен своими исследованиями в области геометрии, механики и арифметики. В частности, он разработал многочисленные методы решения уравнений и систем уравнений, а также внес значительный вклад в теорию чисел.

Архимед разработал множество способов решения квадратных уравнений, применяя геометрические методы. Он также занимался исследованием кубических уравнений и уравнений четвертой степени. Архимед использовал методы, основанные на геометрических принципах, чтобы найти корни этих уравнений.

Однако, помимо работы в области алгебры, Архимед также внес огромный вклад в развитие других областей математики. Он изучал свойства спиралей, парабол и эллипсов, создал методы вычисления площади и объема фигур, и доказал множество теорем, которые были основополагающими для развития геометрии.

Таким образом, Греческая математика, особенно благодаря работам Архимеда, сыграла важную роль в развитии алгебры и других областей математики. Его методы и идеи стали фундаментом для последующих математических открытий и исследований.

Вопрос-ответ:

Какая была первая система математических символов и знаков?

Первая система математических символов и знаков была разработана древними шумерами около 2000 года до н.э. Эта система называлась клинопись, и в ней использовались клинописные знаки для обозначения чисел и алгебраических операций.

Кто изобрел арифметику, как мы ее знаем сегодня?

Современная арифметика была разработана арабскими математиками в 9-10 веках. Основной вклад в развитие арифметики внесли аль-Хорезми, известный также как Альгоритм ибн Муса и аль-Хазин. Они внесли значительные изменения в систему цифр и внедрили позиционную систему счисления, которую мы используем сегодня.

Какой вклад в развитие математики внес Декарт?

Рене Декарт, французский математик и философ 17 века, внес огромный вклад в развитие математики. Он создал аналитическую геометрию, которая стала основой для дальнейшего развития алгебры и геометрии. Декарт также внес важные изменения в символику и нотацию математики, такие как использование букв для обозначения неизвестных величин и введение действий с алгебраическими выражениями.

Кто изобрел символы «плюс» и «минус»?

Символы «плюс» и «минус» были введены в математику арабскими математиками в 9-10 веках. Раньше для обозначения сложения и вычитания использовались слова на арабском языке. Аль-Хорезми, один из величайших арабских математиков, ввел символы «+» и «-» для обозначения операций сложения и вычитания, что существенно упростило запись математических выражений и сделало их более компактными.

Какая система счисления была использована в Древнем Египте?

В Древнем Египте использовалась десятичная система счисления, основанная на использовании различных символов для обозначения чисел от 1 до 9. Однако, в отличие от современной системы счисления, у них не было символа для нуля, и каждое число записывалось отдельными символами. Эта система была развита около 3000 года до н.э. и использовалась до прихода арабской позиционной системы счисления.

Индийские математики: открытие системы счисления и алгоритмов

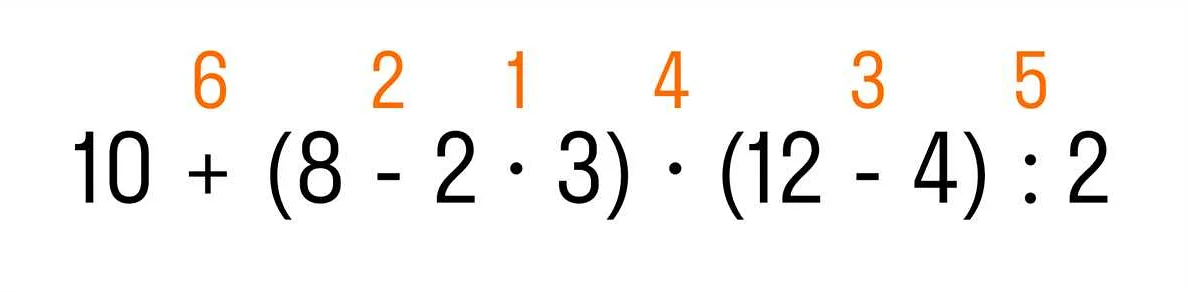
Индийская математика существовала с III века до н.э. и продолжала развиваться на протяжении нескольких веков. Одним из важнейших вкладов индийских математиков было открытие десятичной системы счисления. Вместо использования сложных символов и иероглифов, индийские математики использовали десять цифр, которые мы используем в повседневной жизни: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Это позволило им легко представлять и выполнять сложные вычисления.

Другим открытием индийских математиков был алгоритм деления, который был разработан в IV веке н.э. Этот алгоритм позволял делить числа любой сложности и был основным инструментом для решения сложных математических задач. Он основывался на идее последовательного вычитания и сокращения чисел, чтобы достичь корректного результата.

Индийские математики также изучали и разрабатывали другие алгоритмы, такие как алгоритм умножения и алгоритм вычисления квадратных корней. Они стремились к поиску эффективных и точных методов для выполнения различных математических операций.

Важность открытий индийских математиков в системе счисления и алгоритмах нельзя недооценивать. Эти открытия стали фундаментом современной математики и оказали огромное влияние на развитие этой науки во всем мире.

Средневековая Европа: от открытия алгебры до появления алгоритма операций

В средние века математика в Европе развивалась медленно и неоднородно. Сначала, в V-VI веках, наибольшее влияние на развитие математики оказывали работы арабских ученых, которые в свою очередь переняли знания из древней Греции и Индии.

Первым важным этапом было открытие алгебры в IX-X веках. Основной вклад в развитие алгебры внесли арабские математики, в частности Аль-Хорезми, который написал книгу «Китаб аль-мукабала» («Книга о восстановлении и балансировании»), в которой впервые были изложены правила решения уравнений. Благодаря развитию алгебры возникла возможность решать более сложные математические задачи, включая нахождение неизвестных величин и решение систем уравнений.

В XIV-XV веках в Европе появилась необходимость в упорядочении арифметических операций, что привело к появлению алгоритма операций. Основным вкладом в развитие алгоритма операций является труд итальянского математика Леонардо Фибоначчи. Он написал книгу «Либер абаки» («Книга об абаке»), в которой впервые были описаны и систематизированы арифметические операции, включая сложение, вычитание, умножение и деление.

Благодаря открытию алгебры и появлению алгоритма операций, математика в Средневековой Европе смогла значительно продвинуться вперед. Эти открытия стали основой для дальнейшего развития математики и играют важную роль в современных математических науках.

Построение математической логики: от Декарта до Буля

Развитие математической логики имеет длинную и интересную историю. Одним из важных этапов в этом развитии было построение математической логики от Декарта до Буля.

Рене Декарт, французский математик и философ, играл ключевую роль в формировании математической логики в 17 веке. Он разработал концепцию координатной системы, которая стала основой для аналитической геометрии. Декарт также внес вклад в развитие алгебры, формализуя алгебраические операции и символику. Однако, понятие математической логики как самостоятельной науки еще не сформировалось.

Значительный вклад в развитие математической логики был внесен английским математиком Джорджем Булем в 19 веке. Буль разработал алгебру логики, которая стала основой для дальнейшего развития формальной логики. Он ввел понятие булевой алгебры, в которой операции ор и исключающее или формализованы с помощью символов 0 и 1. Буль также внес вклад в разработку понятий логических операций, таких как отрицание, конъюнкция и дизъюнкция.

Построение математической логики от Декарта до Буля привело к развитию формальной логики как специальной науки, которая изучает принципы правильного рассуждения и вывода. Формальная логика имеет широкое применение в различных областях знания, включая математику, философию, информатику и искусственный интеллект.

Развитие математики в XIX веке: открытие формальной системы операций

В XIX веке математика продолжила свое активное развитие, и одной из важнейших открытий этого периода стало открытие формальной системы операций.

Формальная система операций — это система математических операций, которые должны выполняться в определенном порядке, чтобы получить правильный результат. Это означало, что математики в XIX веке пришли к пониманию, что существует определенная последовательность действий, которую нужно выполнить, чтобы получить правильный ответ на сложные математические проблемы.

Одним из важнейших вопросов, которые стали решаться с помощью формальной системы операций, была проблема решения линейных уравнений. Ранее математики долго искали способы решения уравнений, но благодаря формальной системе операций, они смогли разработать алгоритм, который позволял решить уравнения эффективно и точно.

Помимо решения уравнений, формальная система операций позволила математикам добиться значительного прогресса в других областях математики. Благодаря этому открытию были разработаны новые методы вычислений, а также установлены основы для развития более сложных математических теорий и концепций.

Таким образом, открытие формальной системы операций стало одним из ключевых моментов в развитии математики в XIX веке. Это открытие позволило математикам более эффективно решать сложные математические проблемы, а также сделало возможным развитие более сложных математических теорий и концепций.

Современная математика: от компьютерных алгоритмов до теории категорий

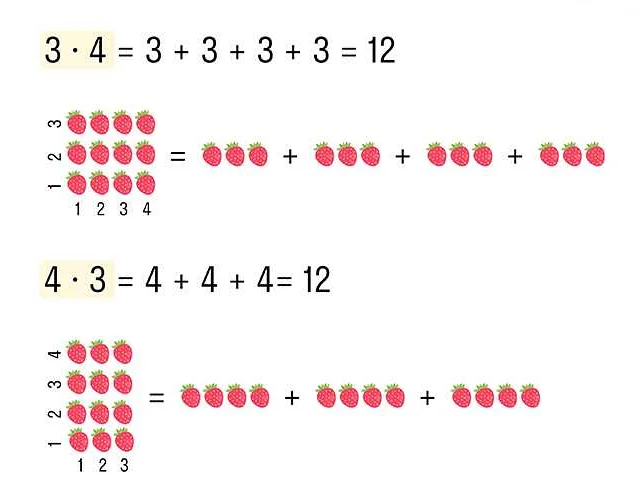
Компьютерные алгоритмы играют огромную роль в современном мире и применяются во многих областях, таких как компьютерная графика, искусственный интеллект, криптография и многое другое. Математики разрабатывают и анализируют эти алгоритмы, чтобы обеспечить их эффективность и точность.

Еще одной важной областью современной математики является теория категорий. Теория категорий является абстрактной математической теорией, которая изучает структуру и связи между различными математическими объектами. Она широко применяется во многих областях математики и физики.

Теория категорий помогает увидеть общие закономерности и связи между различными математическими объектами, что позволяет более глубоко понять их свойства и структуру. Она также играет важную роль в различных приложениях, таких как функциональное программирование и формализация математических теорем.

Современная математика постоянно развивается и находит новые применения в различных областях. Компьютерные алгоритмы и теория категорий являются лишь некоторыми примерами современных математических подходов, которые играют важную роль в современном мире.