Кто придумал задачи по математике

Узнайте, кто придумывает задачи по математике, какие методы они используют и какая роль задач в развитии математического мышления. Узнайте, какие ученые и педагоги внесли вклад в развитие этой области.

Математика – одна из древнейших наук, которая имеет сложную и интересную историю. Возникновение задач по математике было неотъемлемой частью развития этой науки. Первые создатели задач по математике внесли значительный вклад в развитие математики и оставили свои следы в истории.

Одним из первых известных математиков, который создал задачи, был Диофант Александрийский. Он жил в III веке н.э. и стал основателем алгебры. Диофант известен своей работой «Арифметика», в которой он формулировал математические задачи и искал их решения. Он разработал методы решения уравнений и применял их к различным областям знаний.

Еще одним из великих математиков, создавших задачи, был Архимед. Он жил в III веке до н.э. и считается одним из основателей математического анализа. Архимед создал множество геометрических задач, включая известную задачу о нахождении площади круга. Он также разработал методы решения задач, основанные на принципах механики и гидростатики.

Первые создатели задач по математике оставили свой след в истории и сделали значительный вклад в развитие этой науки.

С течением времени математика стала все более сложной и разнообразной. Великие математики, такие как Эйлер, Гаусс, Ньютон и Лейбниц, продолжали традицию создания задач. Они формулировали новые математические проблемы и разрабатывали методы их решения. Благодаря их работе математика стала одной из наиболее развитых и важных наук.

В заключение можно сказать, что история возникновения задач по математике тесно связана с историей развития самой науки. Первые создатели задач по математике сделали важный вклад в развитие этой науки и оставили свой след в истории. Сегодня задачи по математике остаются важной частью обучения и исследования в этой науке.

Возникновение задач по математике: история и вклад первых создателей

Одним из первых создателей математических задач был Диофант Александрийский, живший в III веке нашей эры. В своей знаменитой работе «Арифметика» Диофант представил множество интересных задач, связанных с теорией чисел. Он стал пионером в области алгебры и формулировал задачи, которые требовали различных математических методов для их решения.

Еще одним из знаменитых создателей задач по математике был Архимед, живший в III веке до нашей эры. Он известен своими геометрическими задачами, в том числе задачами на вычисление площади и объема различных фигур. Архимед был первым, кто начал использовать метод математического доказательства в своих задачах.

Развитие задач по математике продолжалось и в средние века. Именно в этот период появились такие знаменитые математики, как Фибоначчи, Леонардо Пизанский и они сделали огромный вклад в развитие этой области. Фибоначчи, например, известен своей последовательностью чисел, которая стала основой для многих задач и исследований.

Таким образом, первые создатели задач по математике играли важную роль в развитии этой области науки. Их задачи стали отправной точкой для дальнейших исследований и привели к появлению новых методов и концепций в математике.

Античность: первые математические задачи

В античности, уже в древнем Египте и Вавилонии, математика использовалась для решения практических задач. Именно тогда были созданы первые математические задачи, которые требовали применения алгебры и геометрии.

Египтяне использовали математику для вычисления площадей полей и строительства пирамид. Они решали простые задачи, связанные с расчетом площадей треугольников и прямоугольников. Египтяне успешно применяли геометрические методы для определения объемов и площадей различных конструкций.

Вавилонцы также активно использовали математику. Они разработали таблицы, которые позволяли решать сложные алгебраические уравнения. Вавилонцы занимались счетами и торговлей, поэтому им требовались точные вычисления. Их задачи были связаны с торговлей, постройкой и взысканием налогов.

Одним из известных создателей первых математических задач в античности был древнегреческий математик Талес. Он известен своей задачей о высоте пирамиды. С помощью геометрических выкладок и подобия треугольников, Талес смог решить эту сложную задачу.

Таким образом, в античности были созданы первые математические задачи, которые имели практическое применение и требовали применения алгебры и геометрии. Это был важный шаг в развитии математики и стимулировал интерес к изучению этой науки.

Средневековье: математика в эпоху знания

Средневековье, или период с примерно 5-го по 15-й век, оказал значительное влияние на развитие математики. В этот период происходило множество открытий и изобретений, которые стали основой для дальнейшего развития науки.

Одной из важных фигур в развитии математики в средние века был арабский математик Мухаммад ибн Муса аль-Хорезми. Он разработал алгебру и внес значительный вклад в арифметику и тригонометрию. Его работы были переведены на латынь и стали доступны для европейских ученых, что способствовало дальнейшему развитию математики в Западной Европе.

Еще одним важным вкладом в развитие математики в средневековье были работы итальянского математика Леонардо Пизанского, известного также как Фибоначчи. Он ввел в Европу восточные математические концепции, такие как десятичная система счисления и понятие фибоначчиевых чисел. Его работы стали основой для развития алгебры и числового анализа.

Средневековье также было эпохой развития геометрии. Одной из важных фигур в этой области был арабский математик Аль-Хайтам. Он разработал новый подход к геометрии, основанный на использовании векторов и принципе отражения. Его работы оказали большое влияние на развитие геометрии в будущем.

В целом, математика в средневековье была важным инструментом для расширения знаний и развития научных исследований. Работы арабских и европейских математиков этого периода стали основой для дальнейшего развития науки и существенно влияли на его современное состояние.

Эпоха Возрождения: расцвет математических задач

В период эпохи Возрождения, примерно с 14 по 17 века, математика подверглась значительному прогрессу. Великие умы того времени стремились расширить границы своих знаний и понять все больше о мире, в котором мы живем. Это привело к появлению новых и увлекательных математических задач.

Одной из важных фигур этого периода был итальянский математик Леонардо Пизанский, известный также как Фибоначчи. Он внес значительный вклад в развитие алгебры и числовых последовательностей. Его знаменитая последовательность чисел, которая получила его имя, стала основой для решения различных математических задач.

Другой выдающийся математик того времени был немецкий ученый Николай Коперник. Он разработал гелиоцентрическую модель Солнечной системы, представляющую Землю и другие планеты, вращающиеся вокруг Солнца. Коперник использовал математические вычисления, чтобы объяснить движение планет и предсказать их положение в будущем.

В эпоху Возрождения также возникли проблемы, связанные с измерением расстояний и времени. Например, появилась задача о нахождении оптимального пути между двумя точками. Для ее решения были разработаны математические методы, такие как метод касательных и метод экстремума.

Кроме того, эпоха Возрождения была переломным моментом в истории математики, когда стали появляться первые математические журналы, в которых ученые могли публиковать свои исследования и обмениваться новыми идеями. Это способствовало более быстрому распространению математических задач и их решений.

Таким образом, эпоха Возрождения стала своеобразным расцветом математических задач. Великие умы того времени внесли значительный вклад в развитие математики и оставили наследие, которое продолжает вдохновлять исследователей и учеников до сегодняшнего дня.

Наука в XVII веке: математические задачи и новые исследования

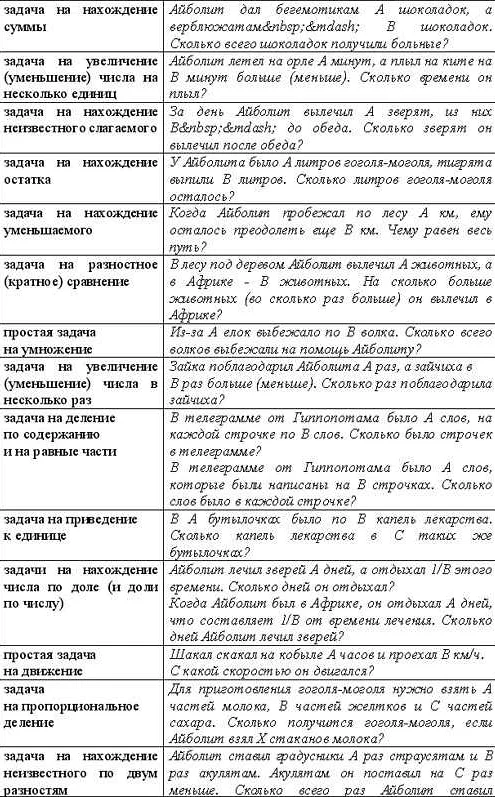
В XVII веке научное развитие сильно ускорилось, и математика стала одной из ведущих наук. Великие умы того времени внесли значительный вклад в развитие математических задач и новых исследований.

Одним из самых значимых математиков того времени был Рене Декарт. Он разработал систему координат и аналитическую геометрию, что позволило решать множество задач, связанных с геометрией. Кроме того, Декарт ввел понятие алгебраического уравнения и разработал методы их решения.

Еще одним выдающимся математиком того времени был Исаак Ньютон. Он разработал дифференциальное и интегральное исчисление, что позволило решать сложные задачи из физики и механики. Ньютон также занимался исследованиями в области оптики и гравитации.

В XVII веке также были проведены важные исследования в области вероятности и статистики. Блез Паскаль и Пьер де Ферма разработали теорию вероятностей, что нашло применение в решении задач с неизвестными данными. Их работы были основополагающими для статистического анализа данных.

В результате всех этих исследований, математика стала неотъемлемой частью научного исследования. Она стала основой для решения сложных задач в различных областях знания.

МатематикВклад

Рене Декарт	Разработка системы координат и аналитической геометрии, введение понятия алгебраического уравнения
Исаак Ньютон	Разработка дифференциального и интегрального исчисления, исследования в области оптики и гравитации
Блез Паскаль и Пьер де Ферма	Разработка теории вероятностей, основы статистического анализа данных

XVIII век: преобразование математических задач

В XVIII веке математические задачи претерпели значительные изменения, благодаря вкладу выдающихся ученых того времени. Одним из таких ученых был Леонард Эйлер. Он сделал значительный вклад в развитие алгебры, геометрии и анализа, а также в создание математических задач.

Эйлер разработал новые методы решения задач, которые стали основой для многих последующих исследований. Он разработал технику разложения задач на более простые составляющие и использовал алгебру и геометрию для их решения. Этот подход к решению задач стал известен как «эйлеровский метод».

Другим выдающимся математиком XVIII века был Карл Фридрих Гаусс. Он внес значительный вклад в различные области математики, включая арифметику и алгебру. Фундаментальные идеи Гаусса по преобразованию математических задач стали фундаментом для развития новых методов решения сложных задач.

Кроме того, в XVIII веке развитие математических задач было способствовано развитию общественных наук, таких как экономика, политика и социология. Математические модели и методы решения задач стали широко применяться в этих областях, что привело к появлению новых типов задач, требующих новых подходов и методов.

Таким образом, XVIII век стал периодом преобразования математических задач благодаря вкладу выдающихся ученых, таких как Леонард Эйлер и Карл Фридрих Гаусс. Их работы и идеи по преобразованию задач стали фундаментом для развития современной математики и ее приложений.

XIX век: углубление в математические задачи

В XIX веке математика продолжила развиваться, и задачи стали выделяться в отдельное направление научных исследований. В этот период были созданы множество сложных математических задач, которые требовали глубокого понимания и детального анализа.

Одним из важных событий в математике XIX века было открытие неевклидовой геометрии. Эта новая область математики изменила представление о пространстве и времени, и привнесла новые задачи и вопросы для исследования.

В XIX веке также были опубликованы работы, которые решали долгое время неразрешимые задачи. Например, в 1859 году немецкий математик Бернхард Риман доказал гипотезу Римана, которая касалась распределения простых чисел. Это был один из наиболее сложных математических вопросов своего времени.

В XIX веке было также создано новое математическое направление — теория групп. Она изучает свойства и структуры групп, которые являются абстрактными математическими объектами. Развитие теории групп привело к решению множества задач в различных областях математики и физики.

В целом, XIX век стал переломным периодом в развитии математики, когда появились новые сложные задачи и новые методы их решения. Углубление в математические задачи позволило не только расширить границы научных знаний, но и повлияло на развитие других областей науки и техники.

XX век: развитие математических задач и новые подходы

В XX веке математические задачи продолжили развиваться, привлекая внимание ученых и математиков со всего мира. Новые подходы и методы решения были разработаны, что привело к значительному прогрессу в различных областях математики.

Одним из важных событий XX века в математике было формализация логики и аксиоматического метода. Математики стали стремиться к строгому и формальному изложению математических теорий и доказательств. Это позволило создать надежную основу для дальнейшего развития математики и решения сложных задач.

Второй половине XX века принадлежат успехи в области теории игр, оптимизации и статистики. Исследования в этих областях привели к разработке новых методов решения задач, которые нашли применение в экономике, управлении производством, финансах и других областях.

С появлением компьютеров и развитием вычислительной техники во второй половине XX века математические задачи стали решаться с использованием численных методов и компьютерных моделей. Это позволило решать задачи, которые раньше считались неразрешимыми или требующими огромных затрат времени и ресурсов.

В конце XX века стали активно развиваться исследования в области искусственного интеллекта и машинного обучения. Математические задачи, связанные с обработкой больших данных и анализом информации, стали привлекать все большее внимание ученых и промышленности.

В целом, XX век был периодом интенсивного развития математических задач и новых подходов к их решению. Это время принесло много открытий и достижений, которые продолжают оказывать влияние на современную математику и нашу жизнь в целом.

Современность: математические задачи в цифровую эпоху

С появлением цифровых технологий и развитием компьютерной науки, математические задачи стали играть еще большую роль в жизни современных людей. Компьютеры и программное обеспечение позволяют решать сложные математические задачи, которые ранее были недоступны для решения вручную.

Одной из важнейших областей математики в цифровую эпоху является криптография. Криптография занимается созданием и анализом методов защиты информации. Математические задачи в этой области связаны с разработкой шифровальных алгоритмов, которые обеспечивают конфиденциальность и защиту данных. Решение этих задач требует умения работать с большими числами, применять алгоритмы шифрования и анализировать сложные математические модели.

Еще одной важной областью математики в цифровую эпоху является искусственный интеллект и машинное обучение. Математические задачи в этой области связаны с разработкой алгоритмов и моделей, которые позволяют компьютерам «учиться» на основе больших объемов данных и принимать решения без явного программирования. Решение этих задач требует умения работать с вероятностными моделями, статистическими методами и алгоритмами машинного обучения.

Также в цифровую эпоху появилась новая область математики — квантовые вычисления. Квантовые вычисления основаны на принципах квантовой механики и позволяют решать задачи, которые классические компьютеры не могут эффективно решить. Математические задачи в этой области связаны с разработкой алгоритмов и протоколов, которые позволяют использовать квантовые системы для решения сложных задач вычислительной математики.

Таким образом, в современности математические задачи играют важную роль в различных областях науки и технологий. Они требуют применения сложных математических моделей, алгоритмов и вычислительных методов. Решение этих задач способствует развитию науки, технологий и обеспечивает прогресс в различных областях человеческой деятельности.

Вопрос-ответ:

Кто является первыми создателями задач по математике?

Первыми создателями задач по математике считаются древние греки. Они начали развивать математику и формулировать задачи еще в V веке до н.э. Известные математики того времени, такие как Пифагор, Евклид и Архимед, внесли значительный вклад в развитие математических задач и вопросов.

Какой вклад внес Пифагор в появление задач по математике?

Пифагор известен как основатель пифагорейской школы, которая занималась изучением математики. Он сформулировал множество задач, связанных с геометрией и арифметикой. Одна из самых известных задач, связанных с Пифагором, это «Теорема Пифагора», которая рассматривает отношение сторон прямоугольного треугольника.

Какой вклад внес Евклид в развитие математических задач?

Евклид, известный греческий математик, приложил много усилий для развития математических задач. Он известен своей работой «Элементы», которая содержит множество геометрических задач и доказательств. Евклид также разработал методы решения задач, основанные на принципе познания и аксиоматическом подходе.

Какой вклад в развитие математических задач внес Архимед?

Архимед, великий древнегреческий ученый, внес важный вклад в развитие математических задач. Он разработал методы для вычисления площадей и объемов, которые использовались для решения различных задач. Одна из наиболее известных задач, связанных с Архимедом, это «Золотая корона», в которой он использовал методы интегрирования для определения объема необычной формы короны.

Какие еще народы внесли вклад в развитие математических задач?

Помимо древних греков, другие народы также внесли вклад в развитие математических задач. Например, древние египтяне разработали методы для решения арифметических задач, связанных с вычислением площадей и объемов. Индийские математики также внесли значительный вклад в развитие алгебры и теории чисел.

Видео по теме: