Структура задач по математике: расшифровка каждой части

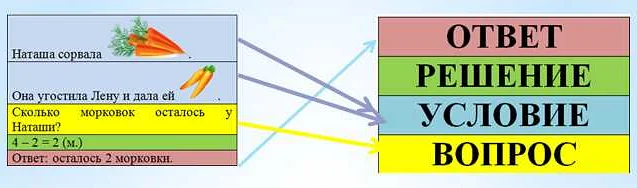
Задача по математике представляет собой ситуацию, которая требует решения математической проблемы с использованием определенных знаний и навыков. В состав задачи входят условие, данные и вопрос, на который необходимо найти ответ. Решение задачи может быть представлено в виде численной величины, формулы или графика. Понимание составляющих задачи поможет ученикам лучше разобраться в математических темах и успешно справиться с заданиями в школе и на экзаменах.

Математика – это один из ключевых предметов в школе, который насквозь пронизывает нашу жизнь. Чтобы хорошо усвоить математику, нужно понимать ее структуру и основные составляющие задач.

Задачи по математике состоят из нескольких основных элементов:

• Условие задачи. Это текстовый вопрос, который определяет задачу и содержит всю необходимую информацию, чтобы ее решить. Он может быть коротким или длинным, простым или сложным.
• Данные. Это числа, факты или информация, которые необходимы, чтобы решить задачу. Они могут быть целыми или дробными, положительными или отрицательными, и так далее.
• Искомое. Это то, что необходимо найти в задаче. Это может быть ответ на вопрос, конкретное число или формула.
• Решение задачи. Это последовательность шагов по получению ответа. Решение может быть самым разным – от простого до сложного – и зависит от типа задачи и ее уровня.

Если вы понимаете структуру и составляющие математических задач, вы сможете повысить свою математическую грамотность и стать лучше в решении задач.

Виды задач в математике

В математике существует множество различных видов задач, каждый из которых требует своего рода решения и подхода.

Арифметические задачи – это задачи, связанные с основными арифметическими действиями (сложением, вычитанием, умножением и делением). Такие задачи можно встретить как на начальных, так и на более высоких уровнях обучения.

Геометрические задачи – это задачи, требующие знания геометрии, включающие в себя нахождение площади, периметра, объема, расстояний и т.д.

Алгебраические задачи – задачи, связанные с алгеброй, объектами которой являются алгебраические выражения, уравнения и системы уравнений.

Вероятностные задачи – это задачи, связанные с вероятностными расчетами, включающие в себя расчет вероятности наступления событий, связанных со случайной величиной.

Статистические задачи – это задачи, связанные с статистическим анализом данных, включающие в себя построение диаграмм, расчет статистических мер и т.д.

Оптимизационные задачи – это задачи, связанные с изучением оптимизации (максимизации или минимизации) некоторых параметров при ограничениях на другие параметры.

Логические задачи – это задачи, требующие знания логики, включающие в себя решение головоломок, задач на выведение логических заключений, задач на построение логической цепочки рассуждений и т.д.

Каждый вид задач подразумевает определенный набор знаний и умений, поэтому изучение каждой из этих задач является необходимой частью математического обучения.

Видео по теме:

Цели решения математических задач

Решение математических задач – это процесс, который помогает нам научиться абстрактному мышлению, логическому анализу и умению применять знания на практике. Цель решения математических задач связана с развитием этих навыков и способностей.

Одной из основных целей решения математических задач является обучение поиску решения проблем. Каждая задача – это новая проблема, которую необходимо решить. При решении задач мы учимся рассуждать логически, искать различные варианты решения и выбирать оптимальный.

Еще одной целью решения математических задач является развитие математического мышления. При решении задач мы применяем полученные знания в новых ситуациях, учитываем условия и ограничения, ищем решения, опираясь на логику и математические законы.

Кроме того, решение математических задач помогает нам осознать важность математики в нашей жизни. Математические задачи возникают повсюду: в экономике, физике, биологии, программировании и во многих других областях науки и жизни. Решая задачи, мы учимся применять математику на практике и осознаем ее важность и применимость.

В целом, решение математических задач поможет нам развивать навыки и способности, необходимые для успешной жизни и работы. Ведь с помощью математических знаний и умений мы можем решать проблемы, принимать взвешенные решения и достигать поставленных целей.

Анализ задачи перед решением

Перед началом решения задачи необходимо провести ее анализ. Во время анализа задачи нужно понять, что именно от нас требуется и как это сделать. Иногда необходимо переформулировать условие или искать дополнительные данные для решения задачи.

Шаги анализа задачи:

• Внимательно читаем условие задачи;
• Определяем, что именно требуется найти или решить;
• Ищем дополнительные данные, которые могут быть нужны для решения;
• Определяем, какую математическую операцию нужно использовать;
• Выполняем необходимые вычисления и получаем ответ.

Необходимо помнить, что правильный анализ задачи является ключом к успешному решению. Перед началом вычислений нужно убедиться, что имеется полное понимание задачи и проверить необходимые данные.

Если задача содержит несколько частей, то ее анализ нужно проводить для каждой отдельной части.

Заключение

Анализ задачи перед решением — это важный этап, который поможет избежать ошибок и добиться правильного ответа. Следуя простым шагам анализа, можно справиться с задачей любой сложности.

Выбор метода решения задач

Один из главных навыков, который нужен для решения задач по математике — это умение выбрать правильный метод решения. Несмотря на то, что многие задачи могут решаться несколькими способами, определенные методы могут оказаться более эффективными, чем другие.

Первым шагом при выборе метода решения задачи является внимательное изучение условия задачи. Некоторые задачи содержат ключевые слова или идеи, которые могут указать, какой метод решения использовать. Например, приведение дробей к общему знаменателю часто используется для решения задач на сложение и вычитание дробей.

Кроме того, необходимо учитывать тип задачи. Например, задачи на геометрию и алгебру требуют различных методов решения. Задачи на геометрию часто требуют использования теорем и правил геометрии, а задачи на алгебру могут требовать использования формул и уравнений.

Наконец, опыт может помочь определить наиболее подходящий метод решения задачи. Некоторые методы могут быть более знакомы и удобными для решения задач, чем другие. Чем больше опыта в решении задач, тем больше возможностей выбрать правильный метод решения.

И в заключении, следует отметить, что правильный выбор метода решения задачи может существенно упростить ее решение и увеличить вероятность успеха.

Построение плана решения математических задач

При решении математических задач необходимо сначала построить план действий, который поможет достичь искомого решения.

Первый шаг в построении плана — внимательно прочитать условие задачи. Необходимо понять, что известно, что нужно найти и какие данные можно использовать.

Далее следует определить, какие формулы и методы решения могут быть применены в данной задаче. Нужно обратить внимание на данные и выделить ключевые понятия. От этого зависит выбор подходящего метода решения.

После того, как выбран метод решения, необходимо составить план действий, определив последовательность операций и основные шаги, которые будут включены в решение задачи.

Важно помнить, что план действий не является окончательным решением задачи. Он лишь помогает в поиске правильного пути решения и помогает избежать ошибок.

После составления плана нужно приступить к решению задачи, следуя заранее определенному плану и используя все необходимые формулы и методы.

Объяснение шагов решения задач

Решение математических задач – это процесс, который состоит из нескольких шагов. Чтобы правильно решить задачу, нужно правильно определить ее тип, выделить важные данные и применить соответствующий алгоритм.

Первый шаг – это чтение условия задачи. Необходимо внимательно прочитать задачу, чтобы понять, что от вас требуется. При этом надо обращать внимание на ключевые слова, которые помогут определить тип задачи.

Далее следует выделение важных данных из условия задачи. Нужно понимать, какие величины присутствуют в задаче, какие значения они имеют и как они связаны друг с другом. Это поможет выбрать подходящий алгоритм для решения задачи.

После этого можно переходить к решению задачи. Несмотря на то, что каждая задача имеет свои особенности, существует общий алгоритм решения, который включает в себя такие элементы, как построение схемы решения, выбор подходящей формулы или метода решения, а также проверку правильности решения.

Последний шаг – это формулировка ответа. Она должна быть четкой и понятной, а также соответствовать единицам измерения, указанным в задании.

В целом, решение математических задач – это несложный процесс, который требует внимательности, логического мышления и знания основных математических понятий и формул.

Проверка правильности решения задач

После того, как ученик решит задачу, необходимо проверить правильность его решения. Для этого необходимо следовать определенным шагам:

1. Проверить соответствие условию: проверить, соответствует ли полученный ответ условию задачи. Если полученный ответ не соответствует условию, то ученик совершил ошибку в расшифровке условия.
2. Проверить математические действия: проверить, были ли выполнены все необходимые математические действия. Необходимо также проверить правильность выполнения действий (в том числе действий со знаками), а также правильность переноса результатов.
3. Проверить окончательный ответ: проверить правильность окончательного ответа. Он должен соответствовать значению, указанному в решебнике (если используется решебник).
4. Проверить адекватность решения: оценить, насколько адекватным является полученный ответ. Если ответ не адекватен (например, получен отрицательный результат при подсчете количества предметов), то вероятнее всего, ученик допустил ошибку где-то в процессе решения.

Если решение задачи верное, то можно перейти к следующей задаче. Если же была допущена ошибка, нужно разобрать задачу еще раз и проверить, где могла быть допущена ошибка. Восстановив правильную последовательность действий, ученик сможет выполнить задачу корректно.

Решение задач в команде

Работать в команде при решении математических задач очень важно. Коллективный разум и взгляд на проблему со стороны разных людей могут помочь найти нестандартные решения и быстрее найти ответы.

Каждый член команды имеет свою роль в решении задачи. Так, например, один может анализировать условие задачи, другой искать формулы и закономерности, а третий выполнять вычисления или рисовать схемы. Важно, чтобы каждый участник четко понимал свою задачу и выполнял ее наилучшим образом.

Для эффективного решения задачи в команде важно установить четкие правила взаимодействия и распределение ролей. Необходимо уметь слушаться друг друга, готовить критику и быть готовым принимать критику. Также полезно иметь возможность устанавливать приоритеты и перераспределять задачи между участниками в зависимости от текущей ситуации.

• Устанавливайте четкие правила командной работы и распределения ролей
• Слушайте друг друга и умейте принимать критику
• Готовьте критику своих партнеров, но делайте это конструктивно
• Запоминайте, что команда должна действовать вместе и подталкивать друг друга к решению

Математический язык в задачах

Решая задачи по математике, необходимо уметь читать, понимать и правильно использовать математический язык. Как правило, такой язык отличается от языка повседневного общения и содержит множество терминов, формул и символов. Поэтому, чтобы успешно решать математические задачи, нужно усвоить основные понятия и знаки.

Для начала, стоит понять, что каждое математическое понятие имеет свой символ. Например, символ «π» обозначает число Пи, а «x» – неизвестное значение в задаче. Понимание знаков и символов, их корректное использование и применение в задачах помогут правильно решить поставленную задачу.

Также необходимо уметь читать и понимать математические формулы. Формулы – это записи математических свойств и законов в компактном виде. Чтение формул требует знания алгебраических и геометрических понятий. Знание формул помогает составлять уравнения, решать системы уравнений и производить расчеты.

• Например, формула площади круга: S = πr², где «S» – площадь круга, «π» – число Пи, «r» – радиус круга. Для решения задач на вычисление площади круга достаточно знать эту формулу;
• Другой пример – формула нахождения среднего арифметического чисел: A = (a₁ + a₂ + … + aₙ)/n, где «A» – среднее арифметическое, «a₁, a₂, … , aₙ» – числа, а «n» – их количество. Зная эту формулу, можно решить задачу на нахождение среднего арифметического нескольких чисел.

Кроме того, для правильного решения задач необходимо понимать математические термины и их определения. Например, «логарифм» – это функция, обратная функции возведения в степень. «Производная» – это скорость изменения функции во времени или в пространстве. Знание математических терминов позволит не сбиваться с толку в процессе решения задач и не допускать ошибки при составлении уравнений и формул.

Поэтому, основная задача при изучении математики – понимание языка, на котором сформулированы задачи. Только тогда можно правильно составить уравнение и решить его, грамотно проанализировать данные и найти верное решение задачи.

Ошибки, которые нужно избегать при решении задач

Решение математических задач может быть непростой задачей, особенно если вы только начинаете знакомиться с ними. Но даже опытные математики могут допускать ошибки при решении задач. В этом разделе мы рассмотрим некоторые распространенные ошибки, которые нужно избегать при решении математических задач.

Не читать условие задачи до конца

Один из самых распространенных способов сделать ошибку при решении задачи — это не продуманный подход к ее условию. Часто студенты читают только начало условия и уже начинают решать, предполагая элементарность задачи. Важно читать и понимать условие задачи до ее решения, иначе вы можете упустить важные детали и неправильно понять, что нужно решить.

Не проверять свою работу

Если вы допустили ошибку в решении математической задачи, это не означает, что вы не сможете ее успешно решить — важно просто внимательно проверить свою работу на наличие ошибок. Часто студенты допускают ошибки во время расчетов, забыв перед умножением или делением разделить или умножить все компоненты, использующиеся в задаче.

Использование неверных формул

Другая распространенная ошибка — это использование неверных формул во время решения задачи. Поэтому важно изучать тему, прежде чем пытаться решить задачи в ней. Вы должны понимать концепции, лежащие в основе формул, прежде чем использовать их для решения задач.

Избегайте этих распространенных ошибок и думайте о каждом шаге, который вы делаете, при решении задач. Только тогда вы сможете успешно решать математические задачи.

Практические советы по решению математических задач

Читайте задачу внимательно

Перед тем, как начать решение математической задачи, важно внимательно прочитать ее текст. Если вы не понимаете, что от вас требуется, лучше перечитайте задачу еще несколько раз, чтобы убедиться, что вы правильно поняли условия задачи.

Разбивайте задачу на составляющие

Если вы понимаете, что от вас требуется, разбейте задачу на составляющие и составьте план действий. Определите, какие формулы и методы вам понадобятся для решения каждой части задачи. Поможет в этом подборка типовых задач.

Используйте аналогии

Иногда для решения задачи можно использовать аналогии. Например, если задача похожа на задачу, которую вы уже решали ранее, то можно использовать тот же метод решения.

Не забывайте проверять свои решения

Проверка своего решения – это важный шаг в решении математических задач. Найдите способ проверки, который подходит для данной задачи. Это может быть простая проверка подстановкой, а иногда проверку можно произвести графически.

• Читайте задачу внимательно
• Разбивайте задачу на составляющие
• Используйте аналогии
• Не забывайте проверять свои решения

Вопрос-ответ:

Какова структура математической задачи?

Структура задачи включает в себя условие, данные и требуемое решение. Условие описывает ситуацию, в которой дана задача, данные — числовые или графические параметры, необходимые для решения, а требуемое решение — ответ на задачу.

Какие составляющие задачи влияют на ее сложность?

Сложность задачи зависит от многих факторов, таких как количество и тип данных, необходимых для решения, логические связи между данными, вид требуемого решения, наличие или отсутствие подсказок, уровень математических знаний, необходимых для решения задачи и др.

Что такое алгоритм решения задачи?

Алгоритм решения задачи — это последовательность действий, которые необходимо выполнить для получения правильного ответа на задачу. Алгоритм может быть различным для разных задач, но должен соответствовать условию и требованиям задачи.

Какова роль формул и уравнений в решении математических задач?

Формулы и уравнения — это математические средства, которые позволяют перевести условие задачи в язык математики, а также решить задачу и получить правильный ответ. Использование формул и уравнений упрощает решение задачи и позволяет сэкономить время.

Как правильно составить уравнение задачи?

Для составления уравнения задачи необходимо проанализировать условие и выделить ключевые моменты. Затем следует использовать известные формулы и математические законы, чтобы выразить неизвестные величины через известные. Наконец, полученное уравнение решается для определения неизвестных величин.

Какова роль графиков в математических задачах?

Графики — это графические представления связей между данными задачи. Они позволяют визуализировать информацию и увидеть соотношения между различными величинами, что упрощает решение задачи. График также может использоваться для проверки правильности решения задачи.

Какими методами можно облегчить решение математических задач?

Существует множество методов, которые помогают упростить решение задачи, например, метод подбора, метод замены переменных, метод пропорций, метод эквивалентных преобразований и др. Также полезно использовать решения аналогичных задач и прибегать к помощи учителя или друга.