Прикладная математика и информатика какие дисциплины изучают

Прикладная математика и информатика – это две важные дисциплины, которые изучаются в области науки и технологий. Прикладная математика занимается применением математических методов и моделей для решения реальных проблем, а информатика – изучает алгоритмы, программирование и обработку информации. Они играют ключевую роль в различных сферах, таких как физика, экономика, компьютерные науки и многих других. Узнайте больше о том, что изучают в этих дисциплинах и как они связаны между собой.

Прикладная математика и информатика являются важными дисциплинами в образовании, которые имеют множество применений в различных сферах жизни. Изучение этих предметов позволяет студентам развивать свои навыки в решении сложных задач, анализе данных и программировании.

Одной из основных дисциплин, изучаемых в области прикладной математики, является математический анализ. Этот предмет позволяет студентам понять основные понятия и методы математического анализа, которые широко применяются в различных научных и технических областях. Изучение математического анализа помогает студентам развить свои навыки в дифференциальном и интегральном исчислении, а также научиться решать задачи с использованием математических методов.

Вместе с математическим анализом студенты изучают также линейную алгебру. Эта дисциплина позволяет студентам понять основы работы с линейными пространствами, векторами и матрицами. Линейная алгебра является важным инструментом в решении задач, связанных с линейными системами уравнений и преобразованиями.

Информатика — это другая важная дисциплина, изучаемая в образовании. Она включает в себя изучение основных понятий и методов программирования, а также алгоритмов и структур данных. Изучение информатики позволяет студентам развивать свои навыки в создании программ и решении сложных задач с использованием компьютерных технологий.

Вместе с программированием студенты изучают также дискретную математику, которая является основой для различных алгоритмических задач. Изучение дискретной математики позволяет студентам понять основные понятия и методы работы с дискретными структурами, такими как графы и деревья, а также научиться формально описывать и анализировать алгоритмы.

Прикладная математика и информатика

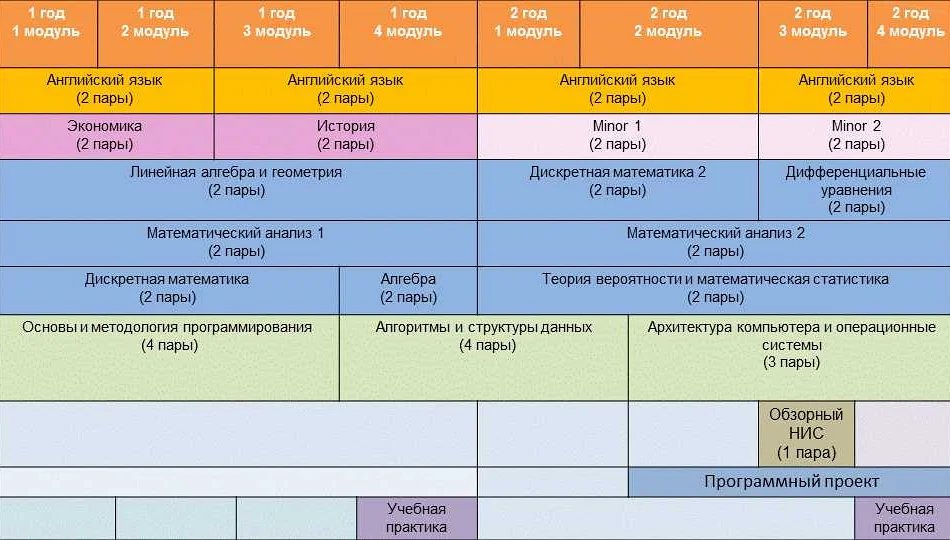
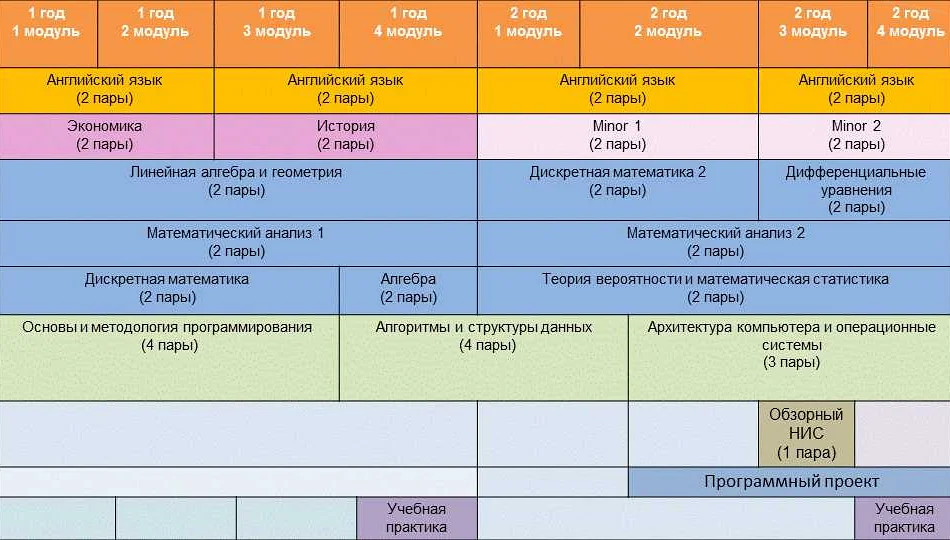
Основные дисциплины, связанные с прикладной математикой и информатикой, включают в себя:

• Математический анализ — изучение математических объектов и операций, таких как функции, пределы и интегралы;
• Линейную алгебру и аналитическую геометрию — изучение алгебраических структур и пространственных объектов;
• Теорию вероятностей и математическую статистику — изучение случайных событий и методов их анализа;
• Дискретную математику — изучение конечных структур и комбинаторики;
• Основы программирования — изучение основных принципов разработки программного обеспечения;
• Алгоритмы и структуры данных — изучение эффективных методов обработки информации;
• Искусственный интеллект и машинное обучение — изучение методов создания интеллектуальных систем и алгоритмов обучения;
• Базы данных и информационные системы — изучение методов организации и хранения данных;
• Моделирование и численные методы — изучение аппроксимационных и численных методов для решения математических задач;
• Оптимизацию и исследование операций — изучение методов оптимизации и принятия решений.

Изучение прикладной математики и информатики позволяет студентам развить навыки математического и логического мышления, а также освоить современные технологии в области информационных технологий. Эта область обеспечивает широкий спектр возможностей для будущей карьеры, включая работу в научных исследованиях, разработке программного обеспечения, анализе данных и многих других областях.

Видео по теме:

Основные дисциплины

Изучение прикладной математики и информатики в образовании включает в себя ряд основных дисциплин, которые позволяют студентам получить необходимые знания и навыки для работы в сфере информационных технологий.

Одной из ключевых дисциплин является «Математический анализ». В рамках этой дисциплины студенты изучают основные понятия и методы математического анализа, такие как пределы и производные функций, интегралы и ряды. Эти знания являются основой для понимания других математических и информатических дисциплин.

Еще одной важной дисциплиной является «Дискретная математика». В рамках этой дисциплины студенты изучают основные понятия и методы дискретной математики, такие как комбинаторика, теория графов и алгоритмы. Эти знания позволяют решать задачи в области информатики и компьютерных наук.

«Алгоритмы и структуры данных» также является важной дисциплиной в изучении прикладной математики и информатики. В рамках этой дисциплины студенты изучают основные алгоритмические методы и структуры данных, такие как сортировка, поиск, хеширование, графы и деревья. Эти знания позволяют эффективно решать задачи обработки и анализа данных.

Кроме того, студенты изучают «Операционные системы», чтобы понять принципы работы операционных систем и научиться эффективно использовать компьютерные ресурсы. Они также изучают «Базы данных», чтобы научиться хранить, обрабатывать и анализировать большие объемы данных.

Важными дисциплинами являются «Программирование» и «Языки программирования», которые позволяют студентам научиться писать программы на разных языках программирования и использовать различные инструменты разработки программного обеспечения.

Также студенты изучают «Теорию вероятностей и математическую статистику», чтобы научиться анализировать сложные системы с помощью вероятностных методов и проводить статистические исследования.

Все эти дисциплины позволяют студентам получить необходимые навыки для работы в сфере информационных технологий и применять их в различных областях деятельности.

ДисциплинаОписание

Математический анализ	Изучение основных понятий и методов математического анализа
Дискретная математика	Изучение основных понятий и методов дискретной математики
Алгоритмы и структуры данных	Изучение основных алгоритмических методов и структур данных
Операционные системы	Изучение принципов работы операционных систем
Базы данных	Изучение основ работы с базами данных
Программирование	Изучение основ программирования
Языки программирования	Изучение различных языков программирования
Теория вероятностей и математическая статистика	Изучение основ вероятностных методов и статистических исследований

Математический анализ

Математический анализ охватывает такие темы, как пределы и непрерывность функций, производные и их приложения, определенные и неопределенные интегралы, ряды и дифференциальные уравнения. Эти концепции являются основой для понимания и решения сложных задач в различных областях науки и техники.

Изучение математического анализа позволяет студентам развить навыки математического моделирования и аналитического мышления. Оно также помогает им усвоить методы и техники решения математических задач, которые могут быть применены в реальных ситуациях.

Важно отметить, что математический анализ является неотъемлемой частью образования в области прикладной математики и информатики. Он является основой для изучения других дисциплин, таких как теория вероятностей, математическая статистика, численные методы и др.

Изучение математического анализа требует от студента серьезного подхода и систематического изучения материала. Оно помогает развить абстрактное мышление, логическое мышление и способность анализировать сложные математические концепции.

В итоге, изучение математического анализа играет важную роль в формировании компетенций студентов в области прикладной математики и информатики. Оно помогает им развить навыки анализа, моделирования и решения сложных задач, а также обеспечивает необходимую математическую базу для успешной работы в различных сферах деятельности.

Дискретная математика

Основные темы, изучаемые в дискретной математике, включают комбинаторику, теорию графов, теорию кодирования, теорию формальных языков и автоматов, а также логику и алгебру.

Комбинаторика занимается изучением различных комбинаторных задач, таких как подсчет комбинаций, перестановок и размещений элементов множества. Теория графов изучает свойства и структуру графов, которые представляют собой совокупность вершин и ребер.

Теория кодирования занимается созданием и анализом кодов, которые используются для передачи информации с минимальной потерей искажений. Теория формальных языков и автоматов изучает формальные языки (например, языки программирования) и автоматы, которые могут их распознавать или генерировать.

Логика и алгебра в дискретной математике используются для формализации и анализа математических структур и рассуждений. Логика позволяет строить формальные доказательства, а алгебра предоставляет инструменты для работы с абстрактными алгебраическими структурами, такими как группы, кольца и поля.

Изучение дискретной математики позволяет развить абстрактное мышление, логическое мышление, умение анализировать и решать сложные задачи. Эта дисциплина также является основой для дальнейшего изучения алгоритмов, теории вычислительной сложности, криптографии и других областей информатики.

Теория вероятностей

Основные понятия теории вероятностей включают вероятность, случайную величину, событие, вероятностное пространство и другие. Вероятность — это числовая характеристика, отражающая степень возможности наступления события. Случайная величина — это математический объект, описывающий результаты случайного эксперимента. Событие — это определенное возможное исходы случайного эксперимента. Вероятностное пространство — это множество всех возможных исходов случайного эксперимента.

Теория вероятностей находит широкое применение в различных областях, таких как статистика, физика, экономика, компьютерные науки и другие. Она позволяет анализировать случайные процессы, предсказывать вероятности различных событий и принимать обоснованные решения на основе вероятностных моделей.

В изучении теории вероятностей студенты изучают основные теоретические понятия, методы решения задач и прикладные аспекты. Они изучают различные вероятностные модели, статистические законы, методы статистического анализа данных и другие темы. Эти знания и навыки позволяют студентам применять теорию вероятностей в практических задачах и исследованиях.

Изучение теории вероятностей является важной частью образования по прикладной математике и информатике. Она помогает студентам развивать аналитическое мышление, логическое мышление и навыки решения проблем. Теория вероятностей также является основой для изучения других дисциплин, таких как математическая статистика и теория игр.

Линейная алгебра

Линейная алгебра включает в себя такие темы, как векторы, матрицы, операции над ними, системы линейных уравнений, базисы и размерность линейных пространств, собственные значения и собственные векторы, линейные преобразования и многое другое.

Одной из важных задач линейной алгебры является решение систем линейных уравнений, которые возникают во многих областях, таких как экономика, физика, компьютерная графика и машинное обучение. Знание линейной алгебры позволяет анализировать и решать такие задачи эффективно и точно.

Линейная алгебра также тесно связана с другими математическими дисциплинами, такими как аналитическая геометрия и математический анализ. Она является фундаментальной основой для более сложных математических понятий и методов, используемых в информатике и прикладной математике.

В изучении линейной алгебры студенты знакомятся с основными понятиями и методами, развивают навыки работы с векторами и матрицами, учатся анализировать и решать системы линейных уравнений. Эти знания и навыки являются неотъемлемой частью образования в области прикладной математики и информатики.

Алгоритмы и структуры данных

Алгоритмы представляют собой последовательность шагов, которые позволяют решать определенную задачу. Они являются основой компьютерных программ и позволяют эффективно обрабатывать данные.

Структуры данных определяют способ организации и хранения информации. Они позволяют эффективно манипулировать данными и упрощают процесс программирования.

Изучение алгоритмов и структур данных позволяет студентам развить навыки анализа и проектирования программного обеспечения. Они учатся создавать эффективные алгоритмы, выбирать подходящие структуры данных и оптимизировать производительность программ.

Основные темы, изучаемые в рамках данной дисциплины, включают в себя:

Анализ сложности алгоритмов	Структуры данных в языках программирования
Сортировка и поиск	Деревья и графы
Динамическое программирование	Хэширование
Генетические алгоритмы	Алгоритмы машинного обучения

Изучение алгоритмов и структур данных является важной частью образования в области прикладной математики и информатики. Это помогает студентам развить навыки решения сложных задач и подготовиться к работе в сфере разработки программного обеспечения.

Оптимизация

Оптимизация применяется во многих сферах, включая экономику, инженерию, логистику, физику и многие другие. Она позволяет оптимизировать процессы производства, распределение ресурсов, управление системами и принятие решений.

В области прикладной математики и информатики, оптимизация включает в себя различные методы, такие как математическое программирование, динамическое программирование, эволюционные алгоритмы и другие. Эти методы позволяют решать задачи оптимизации на основе математических моделей и алгоритмов.

Оптимизация имеет широкий спектр применения, начиная от оптимизации производственных процессов и логистики, заканчивая оптимизацией работы компьютерных сетей и алгоритмов. Она играет важную роль в разработке и улучшении программного обеспечения, а также в проектировании и оптимизации систем и процессов.

Для успешного решения задач оптимизации необходимо уметь формулировать задачи и строить математические модели, а также применять соответствующие методы и алгоритмы. При этом важно учитывать ограничения и особенности конкретной задачи, а также проводить анализ полученных результатов.

Оптимизация является неотъемлемой частью изучения прикладной математики и информатики. Она позволяет развивать аналитическое мышление, умение решать сложные задачи и применять полученные знания на практике.

Теория информации

В рамках теории информации изучаются различные аспекты передачи информации, включая ее кодирование, сжатие, декодирование и распознавание. Также рассматриваются вопросы обнаружения и исправления ошибок при передаче информации.

Одной из ключевых задач теории информации является измерение количества информации. Для этого вводится понятие информационной энтропии, которая позволяет оценить количество информации, содержащейся в сообщении.

Теория информации является основой для различных областей, связанных с передачей и обработкой информации, включая компьютерные сети, телекоммуникации, криптографию и машинное обучение.

Изучение теории информации в образовании позволяет студентам развить навыки анализа и обработки информации, а также понять основы работы с данными и алгоритмами.

Основные темы, изучаемые в теории информации:

• Информационная энтропия
• Кодирование и сжатие информации
• Теория кодов
• Канальное кодирование
• Корректировка ошибок
• Теория случайных процессов

Изучение теории информации является важным шагом для студентов, стремящихся стать специалистами в области информатики и связанных с ней отраслей.

Вопрос-ответ:

Какие дисциплины изучаются в рамках прикладной математики и информатики?

В рамках прикладной математики и информатики изучаются различные дисциплины, такие как математический анализ, линейная алгебра, дискретная математика, теория вероятностей, математическая статистика, теория графов, алгоритмы и структуры данных, численные методы, теория автоматов и формальных языков, и другие.

Зачем изучать прикладную математику и информатику в образовании?

Изучение прикладной математики и информатики в образовании имеет несколько важных целей. Во-первых, это позволяет студентам овладеть навыками анализа, моделирования и решения сложных задач. Во-вторых, это дает возможность развить логическое мышление и умение работать с большими объемами данных. В-третьих, это помогает студентам понять основы программирования и использование компьютерных технологий для решения задач в различных областях, таких как экономика, физика, биология и другие.

Какие навыки можно получить, изучая прикладную математику и информатику?

Изучение прикладной математики и информатики позволяет развить навыки анализа и моделирования, логического мышления и решения задач. Это также дает возможность научиться программированию и работе с компьютерными технологиями. Студенты получат навыки работы с большими объемами данных, использования статистических методов, анализа и визуализации данных. Такие навыки востребованы во многих областях, включая науку, технологии, экономику и финансы.

Какие профессии связаны с прикладной математикой и информатикой?

Изучение прикладной математики и информатики открывает двери к различным профессиям. Студенты могут стать программистами, аналитиками данных, научными сотрудниками, системными аналитиками, консультантами по информационным технологиям, инженерами-математиками, экономистами, статистиками и многими другими. Такие профессии востребованы во многих отраслях, включая IT-сферу, финансы, науку, телекоммуникации, медицину и другие.

Какие дисциплины входят в программу изучения прикладной математики и информатики?

В программу изучения прикладной математики и информатики входят такие дисциплины, как дискретная математика, математический анализ, алгебра и геометрия, теория вероятностей и математическая статистика, математическое моделирование, основы алгоритмизации и программирования, базы данных, компьютерные сети и многое другое.

Какие навыки можно приобрести при изучении прикладной математики и информатики?

При изучении прикладной математики и информатики можно приобрести навыки анализа и решения сложных математических и информационных задач, программирования, работы с базами данных, разработки и оптимизации алгоритмов, а также понимания основных принципов и методов математического моделирования и прогнозирования.