Как решать задачи на смеси и сплавы по математике ОГЭ: пошаговая инструкция и примеры

В статье рассказывается о том, как правильно решать задачи на смеси и сплавы по математике ОГЭ. Описаны основные принципы расчетов и способы их применения. Полезный материал для подготовки к экзамену и повышения уровня знаний в математике.

Задачи на смеси и сплавы являются одними из наиболее сложных для решения в рамках заданий по математике ОГЭ. Более того, их решение может занять много времени и привести к путанице, если вы не знаете некоторых секретов. Поэтому, мы предлагаем вам несколько полезных советов, которые помогут вам быстро и легко решать задачи на смеси и сплавы.

Сначала, важно понимать, что задачи на смеси и сплавы основаны на принципе сохранения массы: изначальный вес смеси или сплава должен быть равен конечному весу. Более того, вы можете использовать принцип сохранения массы, чтобы решить задачи на расчет общего содержания вещества или содержания конкретного вещества в смеси/сплаве.

Также, будьте внимательны при чтении условия задачи. Иногда, условие может содержать лишние данные, которые могут запутать вас и отвлечь от основного вопроса. Поэтому, вы должны читать условие задачи тщательно и выбирать только те данные, которые релевантны решению вопроса.

Важно понимать, что решение задач на смеси и сплавы может быть достаточно простым и быстрым, если вы знаете основные принципы и стратегии. В данной статье мы предоставим несколько примеров и подробных решений задач, которые помогут вам лучше понять важность этих принципов и стратегий.

Как быстро и легко решать задачи на смеси и сплавы по математике ОГЭ?

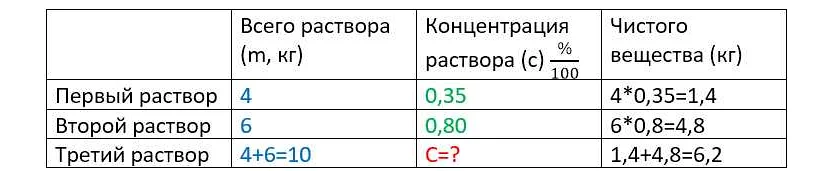
Задачи на смеси и сплавы очень часто встречаются на экзамене по математике ОГЭ, поэтому необходимо уметь быстро и легко решать такие задачи. Для того чтобы решить задачу на смеси, надо понимать, что это за задача и как ее решать.

Перед тем, как начать решать задачу, необходимо внимательно прочитать условие и выделить из него все необходимые данные. Важно также понимать смысл терминов, которые используются в задаче, например, плотность, концентрация, объем и т.д. Это поможет правильно сформулировать условие задачи и выбрать подходящую формулу для ее решения.

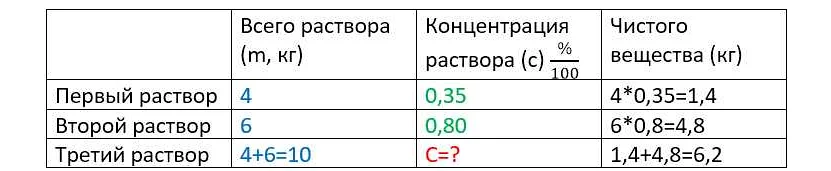
Часто задачи на смеси связаны с таблицами или графиками, поэтому важно уметь правильно их читать и анализировать. Если вы не уверены в своих знаниях, можно использовать таблицу соотношения растворов, которая поможет выбрать подходящую формулу для решения задачи.

Нельзя забывать, что в задачах на смеси и сплавы необходимо следить за единицами измерения и выбирать подходящие формулы для конкретных случаев. Если вы все же столкнулись с непонятными условиями в задаче, необходимо обратиться к учителю или разобраться с задачами по подготовительным курсам.

Основные определения и принципы решения задач на смеси и сплавы

Смесь – это вещество, состоящее из двух или более компонентов.

Сплав – это смесь металлов с целью изменения свойств и улучшения качества их конструкционных материалов.

При решении задач на смеси и сплавы необходимо учитывать следующие принципы:

• Записывайте все начальные данные задачи.
• Используйте формулу смеси для определения процента каждого компонента в смеси.
• Используйте формулу сплава для определения процента каждого металла в сплаве.
• Учитывайте испарение и добавление компонентов.
• Учитывайте изменение свойств при замене компонентов.

Пример задачи на смесь:

В бочку налили 80 литров сока, в котором содержится 20% фруктозы, а затем добавили 20 литров воды. Какой процент фруктозы теперь содержится в смеси?

Решение:

Фруктозы в соке: 80 x 20% = 16 литров.

В смеси всего: 80 + 20 = 100 литров.

Процент фруктозы в смеси: 16 / 100 x 100% = 16%.

Ответ: процент фруктозы в смеси после добавления воды составляет 16%.

Как классифицируются задачи на смеси и сплавы

Задачи на смеси и сплавы являются одними из наиболее распространенных в математике ОГЭ, их можно встретить на практически любом этапе экзамена. Они могут быть разделены на несколько типов, в зависимости от условий задачи:

• Задачи на расчет концентрации вещества в смеси. В таких задачах необходимо рассчитать процентное содержание компонентов в смеси, зная их массы и концентрацию.
• Задачи на расчет количества вещества в смеси. В таких задачах нужно определить количество компонентов в смеси, зная их массы и концентрацию.
• Задачи на составление смеси. В этом случае необходимо определить количество компонентов, которые необходимо смешать, чтобы получить определенную концентрацию смеси.
• Задачи на изменение концентрации. В таких задачах заранее известны базовая смесь и добавляемое количество компонентов, и необходимо рассчитать новую концентрацию.

Помимо этого, задачи на смеси и сплавы часто сопровождаются условиями, имеющими дело с теплоемкостью, плотностью и физическими свойствами компонентов, что добавляет сложности при решении. Однако с помощью правильной формулировки и расчетов задачи на смеси и сплавы можно решить быстро и легко, при условии хорошего знания соответствующих формул и правил расчета.

Решение задач на смеси и сплавы с помощью системы уравнений

Для решения задач на смеси и сплавы, можно использовать систему уравнений, где неизвестными будут количество исходных веществ и их концентрации в итоговом растворе или сплаве.

Например, задача может выглядеть так: из двух смесей, содержащих 20% и 40% спирта соответственно, приготовили 5 литров спиртовой смеси 30%-ной концентрации. Сколько литров каждой исходной смеси было использовано?

Для решения этой задачи можно составить систему из двух уравнений:

• Объем первой смеси: x литров
• Объем второй смеси: y литров
• Концентрация спирта после смешивания: 30%
• Количество спирта в первой смеси: 0,2x литров
• Количество спирта во второй смеси: 0,4y литров

Теперь можно записать систему уравнений:

0,2x + 0,4y = 0,3(x + y)

x + y = 5

Решив эту систему, мы найдем ответ на задачу: x = 3 литра первой смеси, y = 2 литра второй смеси.

Таким образом, использование системы уравнений позволяет решать задачи на смеси и сплавы более эффективно и точно.

Решение задач на сатурацию

Сатурация – это насыщение раствора определенным веществом в таком количестве, при котором дальнейшее добавление этого вещества уже не вызывает изменений состояния раствора. Решая задачи на сатурацию, необходимо знать, как находить объем раствора и количество вещества, которое нужно добавить или извлечь из раствора.

Чтобы решить задачу на сатурацию, необходимо знать концентрацию раствора и его объем. В зависимости от задачи, может быть дано количество добавляемого вещества, концентрация раствора после добавления вещества, или степень насыщения раствора.

Чтобы решить задачу на сатурацию, следует использовать формулу: C1V1 = C2V2, где С1 и C2 – концентрации раствора, V1 и V2 – объем раствора. Если известно количество добавляемого вещества, то используется формула: m = Vc, где m – масса вещества, V – объем раствора, c – концентрация раствора.

Знание формул и практика решения задач помогут разобраться с задачами на сатурацию быстро и легко. Важно также не забывать про правильную запись единиц измерения и округление ответа до нужного количества знаков после запятой.

Задачи на удаление излишков и недостатков со смеси и сплава

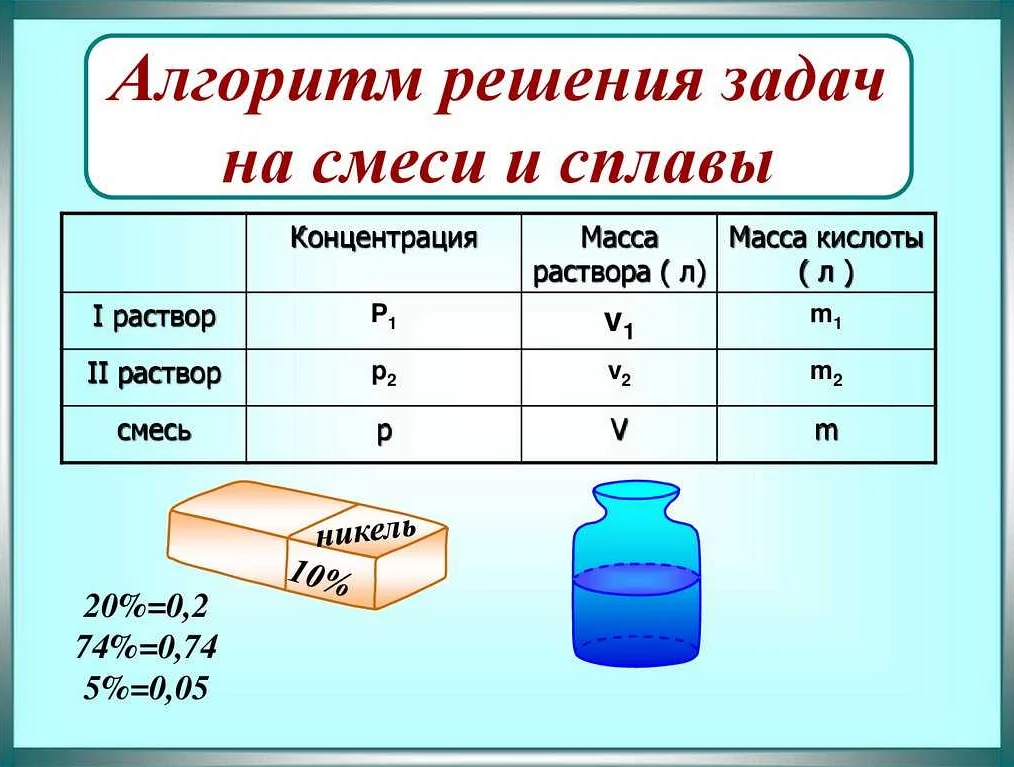
В задачах на удаление излишков и недостатков со смеси и сплава нужно найти количество нужного компонента, чтобы получить смесь или сплав с определенным процентным содержанием.

Для решения таких задач необходимо учитывать процентное содержание компонентов в исходной смеси, а также количество излишков и недостатков, которые нужно удалить или добавить для получения нужного процентного содержания.

Часто в таких задачах используются таблицы, где указывается процентное содержание каждого компонента в исходной смеси, а также необходимое процентное содержание в конечном продукте. Вычисляются необходимые количества компонентов, которые нужно добавить или удалить.

Важно учитывать, что если необходимо удалить излишки, то их содержание вычитается из процентного содержания исходной смеси. Если необходимо добавить недостатки, то их содержание прибавляется к процентному содержанию исходной смеси.

Умение решать задачи на удаление излишков и недостатков со смеси и сплава является ключевым навыком при подготовке к ОГЭ по математике.

Решение задач на процентное содержание компонентов в смеси

Для решения задач на процентное содержание компонентов в смеси необходимо использовать формулы из раздела алгебры. Наиболее употребимыми из них являются:

• Формула процентов: процент = (часть / целое) * 100%
• Формула среднего арифметического: среднее = (сумма всех чисел) / кол-во чисел

При решении задач необходимо учитывать, какие компоненты присутствуют в смеси и как их содержание изменяется при добавлении новых компонентов или вытяжки отдельных компонентов. Кроме того, необходимо учитывать, что проценты компонентов в смеси всегда должны приближаться к 100%

Пример решения задачи: В 30-литровом резервуаре находится смесь молока и воды в соотношении 5:1. Сколько литров молока необходимо добавить, чтобы получить смесь в соотношении 3:1?

Решение:

1. Найдем количество молока и воды в исходной смеси. Применим формулу процентов: 5 / (5+1) * 100% = 83.3% молока и 1 / (5+1) * 100% = 16.7% воды.
2. Найдем, столько молока и воды должно быть в конечной смеси. Так как соотношение молока и воды в конечной смеси 3:1, то получаем, что в конечной смеси должно быть 75% молока (3 / (3+1) * 100%) и 25% воды (1 / (3+1) * 100%).
3. Выразим количество нового молока, которое нужно добавить, используя формулу среднего арифметического: ((5 * 30) + (x)) / (30 + x) * 100% = 75%. Решив уравнение относительно x, получим, что нужно добавить 15 литров молока.

Итак, для получения смеси в соотношении 3:1 нужно добавить 15 литров молока.

Решение задач, связанных с изменением объема смеси или сплава

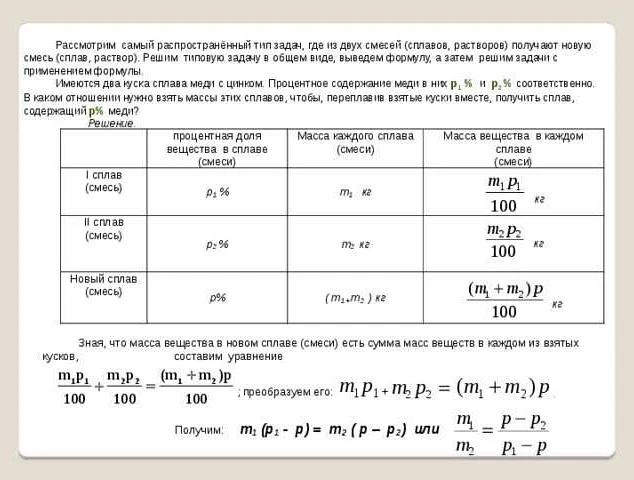
Если в задаче дано изменение объема смеси или сплава, то для решения нужно использовать формулу:

ΔV = V₂ — V₁

далее следует учитывать точный тип смеси или сплава. Например, если задача связана с изменением объема двух жидкостей, то можно воспользоваться формулой:

ΔV = ΔV₁ + ΔV₂ = V₁(1 — ρ₁/ρ) + V₂(1 — ρ₂/ρ)

где ρ₁ и ρ₂ — плотности соответствующих жидкостей, ρ — средняя плотность смеси, V₁ и V₂ — начальные объемы жидкостей.

Если же задача связана с изменением объема сплава, то может быть использована формула:

ΔV = Vα(γ₂ — γ₁)/(γ₂ — γ₁α)

где Vα — объем а, γ₁ и γ₂ — плотности расплавленного металла и сплава соответственно, γ₁α — плотность сплава α.

Важно также не забывать проверять единицы измерения, чтобы получить корректный ответ на задачу.

Примеры решения задач на смеси и сплавы

Задачи на смеси и сплавы являются одними из наиболее распространенных типов заданий на ОГЭ по математике. Часто они вызывают затруднения у учеников, но на самом деле, с их решением можно успешно справиться, следуя определенным правилам.

Рассмотрим пример задачи: «В 20 литрах раствора содержится 12% кислоты. Сколько литров воды следует добавить, чтобы получить 10% раствор?»

Решение:

1. Найдем количество кислоты в исходном растворе:
   • 12% от 20 литров = 2,4 литра кислоты
2. Пусть x — количество добавляемой воды в литрах. Тогда:
   • Конечный объем раствора = 20 + x литров
   • Конечное количество кислоты = 2,4 литра
   • Конечный процент кислоты = 10%
3. Составим уравнение:
   • 2,4 / (20 + x) * 100 = 10
4. Решим уравнение:
   • 2,4 * 100 = 10 * (20 + x)
   • 240 = 200 + 10x
   • 10x = 40
   • x = 4
5. Ответ: воды необходимо добавить 4 литра.

Таким образом, решение задач на смеси и сплавы не так сложно, как может показаться на первый взгляд. Главное — следовать логике и шаг за шагом решать поставленную задачу.

Советы по подготовке к решению задач на смеси и сплавы

1. Правильно составляйте уравнения для решения задач. Следите за правильным расчетом объемов и масс компонентов, при использовании процентных соотношений. Если нужно решить задачу на определение процентного состава смеси или сплава, используйте формулу: процентное соотношение = (масса компонента/общая масса смеси или сплава)*100.

2. Знайте основы химии. Хорошо знание периодической таблицы растительности, важных для решения задач на смеси и сплавы, таких как: молярная масса компонентов, стехиометрия реакций, состав понятие моль и граммовой-эквивалентности.

3. Не забывайте про блок с задачками на смеси и сплавы в учебнике. Решайте их по вашей стратегии, отслеживая, что работает хорошо и что нуждается в дополнительном времени и усилиях. При решении учебных задач, применяйте разные методы решения для разнообразия и учите разнообразные способы решения задач.

4. Практиковать, практиковать, практиковать! Задачи на смеси и сплавы могут быть подстерегают вас на экзаменах, так же как и в повседневной жизни. Примеры и упражнения в работе на дому, тестах и пробных экзаменах помогут вам избежать паники и смело решать задачи на экзамене.

5. Обращайте внимание на единицы измерения в ответах. Если в задаче предоставлены разные единицы измерения, убедитесь, что вы думаете в тех же своих ответах. Правильные единицы измерения помогут вам дать ответ, который можно легко сравнить с другими результатами и проверить его из соответствия.

6. Не забывайте об ошибках округления. Многие задачи на смеси и сплавы могут иметь не очень точные цифры, и в результате вы можете получить не слишком точный ответ. Важно понимать, когда округлять и сколько знаков исправления. Исправьте округление только после окончания решения задачи и проверьте свой ответ на правильность.

Видео по теме:

Вопрос-ответ:

Какие существуют способы решения задач на смеси и сплавы?

Существует несколько способов: метод алгебраических желаний, метод растворения, метод замен величин, метод эквивалентов и т.д. Важно для каждой конкретной задачи выбрать оптимальный метод и работать с ним внимательно.

Какие формулы нужно знать для решения задач на смеси и сплавы?

Для решения задач на смеси и сплавы нужно знать формулы нахождения концентрации вещества в растворе, формулы нахождения процентного содержания вещества в смеси, формулы эквивалентов.

Как выбрать правильно метод решения задачи на смеси и сплавы?

Для выбора метода решения задачи на смеси и сплавы нужно внимательно прочитать условие задачи, определить, какие величины нужно найти и какие известны, а затем выбрать подходящий метод, который даст возможность решить задачу.

Как рассчитать плотность сплава?

Плотность сплава можно рассчитать по формуле p = (масса сплава)/(объем сплава). Также массу сплава можно выразить через массы компонентов сплава и их плотности и подставить в формулу для нахождения плотности сплава.

Какие единицы измерения используются при решении задач на смеси и сплавы?

Единицы измерения, используемые при решении задач на смеси и сплавы — это граммы, миллилитры, проценты, молярные массы.

Как решать задачи на смеси и сплавы с использованием метода эквивалентов?

Для решения задач на смеси и сплавы с использованием метода эквивалентов нужно определить эквивалентные массы компонентов, затем выразить количество одного из компонентов через количество другого и подставить в формулу для нахождения искомой величины.

Как находить процентное содержание веществ в смеси?

Процентное содержание вещества в смеси можно найти, разделив массу данного вещества в смеси на общую массу смеси и умножив на 100%. Формула для вычисления процентного содержания вещества в смеси: % = (масса вещества в смеси)/(общая масса смеси) * 100%

Типичные ошибки при решении задач на смеси и сплавы

Решение задач на смеси и сплавы может быть сложным и требует тщательного анализа. К сожалению, многие студенты делают типичные ошибки, которые могут привести к неверному ответу или даже к провалу экзамена. В этом разделе мы рассмотрим некоторые из наиболее распространенных ошибок при решении задач на смеси и сплавы.

• Не учитывание изменения плотности при смешивании жидкостей. В задачах на смеси и сплавы необходимо учитывать, что при смешивании жидкостей может произойти изменение плотности. Это может привести к тому, что объем смеси не будет равен объему входящих в нее жидкостей.
• Неправильное определение доли компонента в смеси. Ошибки возникают, когда студенты пытаются рассчитать долю компонента в смеси, используя процентное содержание или общий объем смеси. Чтобы решить задачу правильно, необходимо использовать формулу для расчета доли компонента, учитывая исходные данные и конечный результат.
• Неверный выбор единиц измерения. В задачах на смеси и сплавы обычно представлены различные единицы измерения, такие как граммы, миллилитры, проценты и т.д. Необходимо тщательно выбрать соответствующие единицы измерения для всех входных данных и ответов, чтобы избежать ошибок при расчетах.
• Недостаточный анализ условия задачи. Некоторые задачи на смеси и сплавы требуют дополнительного анализа условия, чтобы правильно определить состав исходных компонентов и доли каждого из них. Если необходимо, студенты должны использовать дополнительные формулы и уравнения, чтобы решить задачу.

Избегайте этих распространенных ошибок, тщательно анализируйте условия задач и используйте соответствующие формулы и единицы измерения. Это поможет вам решить задачи на смеси и сплавы правильно и получить хороший балл на экзамене по математике ОГЭ.

Полезные ресурсы для тренировки решения задач на смеси и сплавы

1. Matematika-tutor.ru

На этом сайте собраны базовые понятия по теме смеси и сплавы, которые помогут уверенно решать задачи. Также здесь есть множество примеров, которые помогут понять, как правильно решать разные виды задач и как применять формулы.

2. Сайт ГИА и ОГЭ

На сайте ГИА и ОГЭ можно найти официальные задания, которые будут помогать тренироваться перед экзаменом. Кроме того, здесь также есть решения тестовых заданий, что позволит быстрее понять, как правильно решать задачи на смеси и сплавы.

3. Математика на EgE.Info

Этот сайт поможет углубить знания по математике и изучить теоретический материал по теме смеси и сплавы. Здесь вы найдете различные теоретические материалы, которые подробно описывают, как правильно решать задачи на эту тему.

4. Репетитор по математике

Воспользуйтесь услугами репетитора, который поможет в комфортной обстановке разобраться с темой смеси и сплавы и провести итоговую подготовку перед экзаменом. Репетитор может подобрать индивидуальный подход для каждого ученика и предоставить контрольные работы, которые помогут тренироваться и уверенно решать задачи на экзамене.

5. Учебники по математике

Лучшие учебники по математике содержат подробное описание как решать задачи по смеси и сплавам. В них дается конкретный материал и разное количество примеров. Вы можете найти такие учебники в библиотеках или купить их в магазинах книг или интернет магазинах.