Как решить 13 задание ЕГЭ по математике на базовом уровне: подробный алгоритм и советы
Содержимое
- 1 Как решить 13 задание ЕГЭ по математике на базовом уровне: подробный алгоритм и советы
- 1.1 Как решать 13 задание ЕГЭ по математике базового уровня: полезные советы и примеры решения
- 1.2 Понимание условия задачи
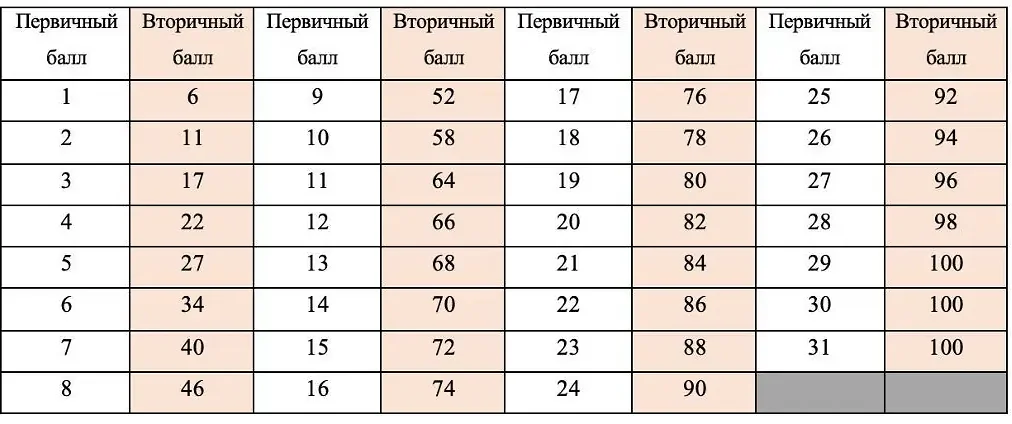
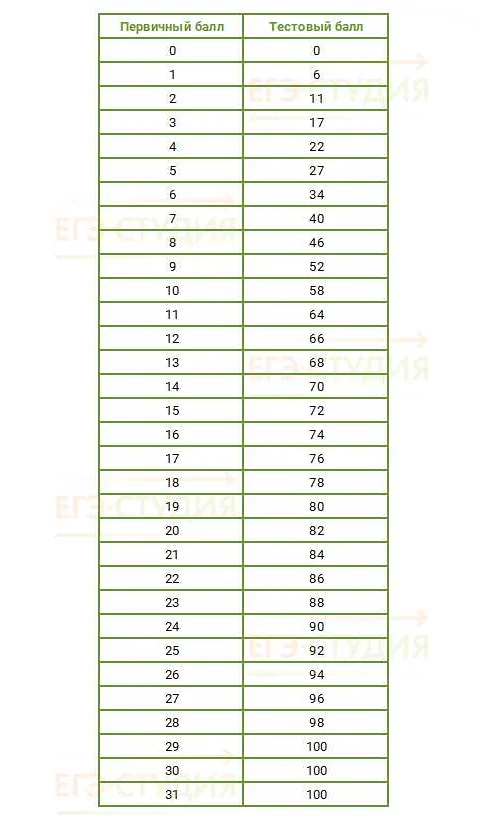
- 1.3 Использование графиков и таблиц
- 1.4 Вычисление вероятностей
- 1.5 Работа с координатной плоскостью
- 1.6 Определение функций
- 1.7 Применение формул и теорем
- 1.8 Решение уравнений и неравенств
- 1.9 Знание геометрических фигур и свойств
- 1.10 Применение формулы Герона
- 1.11 Видео по теме:
- 1.12 Вопрос-ответ:
- 1.12.0.1 Какие существуют типичные ошибки при решении 13 задания ЕГЭ по математике?
- 1.12.0.2 Какую базовую фигуру лучше всего выбрать при решении 13 задания ЕГЭ по математике?
- 1.12.0.3 Как грамотно использовать формулы при решении 13 задания ЕГЭ по математике?
- 1.12.0.4 Как лучше всего готовиться к решению задания?
- 1.12.0.5 Что делать при непонимании условия задачи по 13 заданию ЕГЭ по математике?
- 1.12.0.6 Какие методы можно использовать для проверки правильности решения задания по 13 заданию ЕГЭ по математике?
- 1.12.0.7 Какие существуют особенности решения 13 задания ЕГЭ по математике при экзамене?
- 1.13 Решение задач с пропорциями
- 1.14 Проверка корректности решения
Узнайте, как правильно решать 13 задание по математике на базовом уровне ЕГЭ. В статье вы найдете подробное объяснение алгоритмов решения.
Единый государственный экзамен является одним из самых ответственных моментов в жизни старшеклассников. Среди всех предметов, которые необходимо сдать, математика является одним из самых сложных. И, конечно же, 13 задание — это одно из самых затруднительных. Однако, есть несколько советов, которые могут помочь вам решить эту задачу с легкостью.
Прежде всего, необходимо понимать, что для решения данной задачи важно не только знание математических формул, но и умение грамотно работать с графиками, таблицами и данными. Кроме того, не стоит забывать, что в 13 задании нацелено на проверку не только знаний, но и навыков анализа и синтеза полученной информации.
Если вы хотите успешно сдать ЕГЭ по математике, то не забывайте тренироваться. Делайте контрольные и практикуйте решение задач самостоятельно. Таким образом, вы сможете подготовиться к экзамену наилучшим образом и с легкостью справиться с решением любой задачи, в том числе и 13 задания.
Как решать 13 задание ЕГЭ по математике базового уровня: полезные советы и примеры решения

13 задание ЕГЭ по математике базового уровня — это задание на составление уравнений, графиков и анализ их свойств. Для успешного решения этого задания необходимо иметь соответствующие знания и навыки.
В первую очередь, необходимо внимательно прочитать условие задачи и разобраться в его сути. Затем следует составить уравнение, исходя из условия, и проанализировать свойства графика этого уравнения.
Для решения 13 задания ЕГЭ по математике базового уровня полезно воспользоваться следующими советами:
- Не спешите. Внимательно читайте условие и разбирайтесь с ним.
- Используйте все данные, которые есть в условии задачи.
- Обращайте внимание на знаки в уравнениях и их изменение в зависимости от значений переменных.
- Рисуйте графики на координатной плоскости и анализируйте их свойства.
- Проверяйте свои решения, подставляя изначальные данные в полученные уравнения и проверяя, соответствует ли ответ заданному условию.
Рассмотрим пример решения 13 задания ЕГЭ по математике базового уровня:
Условие: Найдите уравнение прямой, проходящей через точку (-1, 3) и пересекающей ось ординат под углом 45 градусов.
- Составляем уравнение прямой: y = kx + b.
- Так как прямая проходит через точку (-1, 3), то: 3 = k*(-1) + b => b = k+3.
- Так как прямая пересекает ось ординат под углом 45 градусов, то тангенс угла наклона прямой равен 1.
- Таким образом, уравнение прямой имеет вид: y = x + 4.
Проверим полученный ответ, подставив изначальные данные: программа дает ответ на 13 задание ЕГЭ по математике базового уровня, то есть, полученное уравнение прямой является правильным.
Понимание условия задачи
Одной из самых важных составляющих решения задачи является правильное понимание ее условия. Часто бывает, что задача кажется сложной из-за непонятного или запутанного сформулированного условия. Поэтому важно уделить достаточное внимание этому этапу и попытаться проанализировать условие задачи.
Для начала нужно иметь представление о том, что стоит рассматривать в задаче. При этом необходимо обратить внимание на все важные элементы. Важно понимать, какие данные нужны для решения, а какие могут быть избыточными.
Чтобы лучше разобраться с условием задачи, можно воспользоваться различными методами. Например, можно визуализировать условие, изобразив схему или набросок. Также можно использовать переформулирование вопросов или задавать дополнительные вопросы для уточнения условия.
Не стоит забывать, что правильное понимание условия является основой для успешного решения задачи. Если вы сомневаетесь в правильности своего понимания, не стесняйтесь обратиться к учителю или другу для дополнительной помощи и объяснений.
Использование графиков и таблиц
Во время решения задач ЕГЭ по математике полезно использовать графики и таблицы. Графики позволяют наглядно представить зависимость двух переменных, что может помочь лучше понять условие задачи и выбрать правильный алгоритм решения. Таблицы удобны для организации и систематизации данных, поэтому их использование также может существенно упростить решение задачи.
Если задача имеет графическую иллюстрацию, рекомендуется начать с ее анализа. Изучите оси координат, шкалы, точки пересечения и прочие элементы графика. Попробуйте представить найденную информацию в математической форме, а затем используйте ее для решения задачи.
Когда речь идет о таблицах, важно уметь правильно считывать и анализировать информацию из них. Обратите внимание на значения в строках и столбцах, а также на значения, которые вычисляются на основе имеющихся данных. Используйте таблицу как руководство при выполнении задачи, и она поможет вам быстрее и точнее решить ее.
Не забывайте также об использовании формул и алгоритмов. Если вы представили задачу в виде графика или таблицы, можете попробовать вывести соответствующую формулу, которая позволит решить задачу для любых значений.
- Использование графиков и таблиц может значительно упростить решение задач ЕГЭ по математике;
- Анализ графической иллюстрации позволяет наглядно представить зависимость двух переменных;
- Таблицы позволяют организовать данные и использовать их для решения задачи;
- Не забывайте также об использовании формул и алгоритмов для получения более точных результатов.
Вычисление вероятностей

Вероятность – это шанс того, что определенное событие произойдет. Она вычисляется путем деления количества благоприятных исходов на общее количество исходов. В математической терминологии это можно записать так:
P(A) = благоприятные исходы/общее количество исходов
Знание вероятностей необходимо для решения многих задач, в том числе и для задач ЕГЭ по математике. Важно уметь правильно интерпретировать условия задачи и правильно вычислять вероятности.
Существует два типа вероятностей: априорная (теоретическая) и апостериорная (эмпирическая). Априорная вероятность вычисляется на основе теоретических соображений, а апостериорная – на основе опыта. Например, если мы кидаем игральную кость, то априорная вероятность выпадения каждой из ее граней равна 1/6, а апостериорная вероятность – это реальный шанс выпадения каждой грани на практике, который может отличаться от теоретического значения.
Вычисление вероятностей является важным инструментом для решения задачи ЕГЭ по математике. Оно позволяет правильно определять шансы на наступление определенного события и выбрать правильный путь решения задачи.
Работа с координатной плоскостью
Координатная плоскость — важно понимать, что это геометрическая конструкция, состоящая из двух осей – оси абсцисс и оси ординат. На этой плоскости можно изображать геометрические фигуры и задавать координаты точек. Знание основ работы с координатной плоскостью позволяет эффективно решать многие задачи, в том числе и задачи ЕГЭ.
Координаты точек — каждой точке на координатной плоскости соответствуют две координаты — абсцисса и ордината. Обычно, абсцисса обозначается буквой x, ордината — буквой y. Например, точка (2, 3) – это точка на расстоянии 2 от оси абсцисс и 3 от оси ординат.
График функции — график функции – это набор точек на координатной плоскости, которые соответствуют выбранным значениям функции. График функции может быть использован для анализа поведения функции на различных участках и нахождения ее основных характеристик, например, экстремумов, точек перегиба, асимптот и т.д.
Работа с плоскостью — при решении задач, связанных с координатной плоскостью, важно уметь находить расстояния между точками, строить отрезки, сравнивать углы, находить углы поворота фигур и многое другое. Для этого можно использовать геометрические формулы, а также знакомиться с графическими методами решения задач, такими как графический метод решения системы уравнений и метод графического построения функций.
Определение функций
Функция – это математический объект, который связывает элементы двух множеств: области определения и области значений. Область определения – это множество значений, для которых функция определена, а область значений – множество значений, которые функция может принимать.
Функция обозначается буквой f и записывается в виде f(x). Значение x называется аргументом, а значение f(x) – это значение функции в точке x. Любая функция должна удовлетворять свойству однозначности, то есть каждому значению x в области определения должно соответствовать не более одного значения f(x) в области значений.
Функция может быть задана аналитически, графически или в виде таблицы. Аналитическое задание функции происходит путем записи ее выражения, которое может содержать переменные, операции и константы. Графическое задание функции представляет ее в виде графика, который является наглядной интерпретацией значений функции. В табличном виде функция задается списком ее значений в соответствии с определенными аргументами.
- Область определения и область значений должны быть явно указаны в определении функции;
- Функция должна удовлетворять свойству однозначности;
- Функция может быть задана аналитически, графически или в виде таблицы.
Применение формул и теорем

Для решения задачи ЕГЭ по математике базового уровня необходимо знать и уметь применять различные формулы и теоремы. Наиболее важными из них являются:
- Теорема Пифагора, которая утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
- Формулы тригонометрии, позволяющие вычислять значения тригонометрических функций для различных углов.
- Формула Герона, используемая для определения площади треугольника по длинам его сторон.
Расчеты по этим формулам и теоремам могут быть применены к различным геометрическим фигурам и задачам связанным с нахождением расстояний, площадей и объемов. Кроме того, для решения задачиЕГЭ по математике базового уровня часто приходится использовать простейшие законы арифметики и алгебры, такие как закон ассоциативности и закон дистрибутивности.
Чтобы эффективно применять формулы и теоремы при решении задач ЕГЭ, необходимо уметь распознавать ситуации, в которых они могут быть использованы, и знать, какие данные нужны для их применения. Начать стоит с тщательного изучения теоретической части курса математики и систематической тренировки на задачах с постепенным усложнением.
Решение уравнений и неравенств
Решение уравнений и неравенств – одна из важнейших тем в математике. Для решения уравнений необходимо уметь применять различные алгебраические операции, знать свойства и изменения знаков в соответствии с правилами алгебры.
Для решения неравенств важно понимать различия между неравенствами с односторонним и двухсторонним знаком. Неравенства также могут быть решены с применением алгебраических приемов и правил, а также путем графического отображения на числовой прямой.
Для более эффективного решения уравнений и неравенств можно использовать таблицы и схемы для отображения возможных значений переменных и изменения знаков. Также полезно освоить методы последовательных приближений и анализа корней, чтобы быстрее и точнее получать ответы.
- Пример уравнения: 2x + 5 = 13
- Решение: 2x + 5 — 5 = 13 — 5, 2x = 8, x = 4
- Пример неравенства: x + 3 > 7
- Решение: x + 3 — 3 > 7 — 3, x > 4
При решении уравнений и неравенств необходимо быть аккуратными и внимательными, делать правильные выводы и не ошибаться в арифметике. После решения задачи важно проверить ответы на корректность и соответствие условию.
Знание геометрических фигур и свойств
Для успешного решения заданий ЕГЭ по математике базового уровня необходимо хорошо знать геометрические фигуры и их свойства. Например, знание как построить высоту, биссектрису, медиану треугольника поможет решить многие задания из геометрии.
Также, необходимо уметь работать с формулами для нахождения площади и периметра различных фигур. Например, формулы для прямоугольника, круга, треугольника и т.д. часто используются в заданиях ЕГЭ.
Важно понимать свойства параллелограмма, ромба и трапеции, так как они часто встречаются в заданиях на нахождение площади или периметра фигуры. Также, знание формул для объема и площади поверхности призмы, пирамиды и шара может помочь в решении заданий из геометрии.
- Необходимо хорошо знать геометрические фигуры и их свойства
- Умение работать с формулами для нахождения площади и периметра различных фигур является важным
- Параллелограмм, ромб, трапеция и другие фигуры нужно знать и понимать их свойства
- Формулы для объема и площади поверхности призмы, пирамиды и шара могут помочь в решении заданий
Применение формулы Герона

Формула Герона позволяет находить площадь треугольника, зная длины его сторон. Данная формула может быть полезна при решении 13 задания ЕГЭ по математике базового уровня, где часто предлагается найти площадь треугольника.
Формула Герона имеет простой вид:
S = √(p(p-a)(p-b)(p-c))
где S – площадь треугольника, p – полупериметр треугольника, a, b, c – длины сторон.
Для применения данной формулы нужно сначала найти полупериметр треугольника:
p = (a + b + c)/2
После этого можем подставить значения длин сторон треугольника в формулу Герона и найти площадь. Важно не забывать про порядок вычислений, особенно при использовании калькулятора.
Применение формулы Герона позволяет эффективно и быстро решать задачи на нахождение площади треугольника в рамках ЕГЭ по математике базового уровня.
Видео по теме:
Вопрос-ответ:
Какие существуют типичные ошибки при решении 13 задания ЕГЭ по математике?
Одной из наиболее распространенных ошибок является использование неправильной формулы для нахождения объема тела. Также многие студенты не учитывают наличие углов и ребер у тела, что приводит к неверному результату. Другой распространенной ошибкой является неправильный выбор базовой фигуры для нахождения объема.
Какую базовую фигуру лучше всего выбрать при решении 13 задания ЕГЭ по математике?
Лучше всего выбирать базовую фигуру с наибольшей симметрией и наиболее простой формой. Например, если тело имеет форму правильного треугольника, то лучше всего выбрать призму или пирамиду, основанием которой является треугольник. В таком случае объем будет легко вычислим.
Как грамотно использовать формулы при решении 13 задания ЕГЭ по математике?
Перед тем, как приступать к решению задания, необходимо вспомнить основные формулы для вычисления объема тел. При выборе формулы необходимо учитывать форму и размеры тела. Если формула не подходит для данной фигуры, то необходимо заменить ее на более подходящую.
Как лучше всего готовиться к решению задания?
Лучше всего готовиться к решению задания практикой. Необходимо брать различные фигуры и находить их объем по изученным формулам. Важно также уметь быстро определять базовую фигуру для нахождения объема сложных тел, так как на экзамене на это будет отводиться ограниченное время.
Что делать при непонимании условия задачи по 13 заданию ЕГЭ по математике?
Если вы не понимаете условие задачи, лучше всего перечитать его еще несколько раз и распробовать его переформулировать. Если это не помогает, то стоит обратиться к учителю или спросить у товарища, который уже справился с заданием. Главное не паниковать и не терять время на бесполезные размышления.
Какие методы можно использовать для проверки правильности решения задания по 13 заданию ЕГЭ по математике?
Один из методов – это перепроверка всех вычислений и переделывание задания сначала. Также можно использовать метод «обратной подстановки», когда найденный объем возвращают в исходное условие и проверяют, совпадает ли результат.
Какие существуют особенности решения 13 задания ЕГЭ по математике при экзамене?
На экзамене для решения 13 задания выделяется только 4 минуты. При этом могут предоставляться различные формулы и таблицы. Однако, необходимо помнить, что они могут быть неполными или содержать ошибки. Важно также уметь быстро находить базовую фигуру для нахождения объема тела.
Решение задач с пропорциями
Задачи с пропорциями — один из разделов математики, который часто встречается на ЕГЭ по математике базового уровня. Для решения задач необходимо знать определение пропорции и уметь применять ее свойства.
Пропорцией называют равенство двух отношений. Если дано четыре числа, a, b, c и d, то их можно записать в виде двух отношений: a/b и c/d. Если эти отношения равны, то получается пропорция a:b = c:d.
Для решения задач с пропорциями необходимо использовать свойства пропорций. Она гласит:
- Если два отношения a/b и c/d пропорциональны, то их можно умножить друг на друга: a/b = c/d ⇒ a ⋅ d = b ⋅ c;
- Если пропорциональные отношения a/b = c/d, то их можно поставить в соответствие с общим множителем k: a = k ⋅ b и с = k ⋅ d.
Одним из примеров задач с пропорциями является задача про расстояние между двумя городами. Рассмотрим ее решение:
| Условие: | Расстояние между городами А и В равно 200 км. Автомобиль, двигаясь со скоростью 50 км/ч, проехал это расстояние за некоторое время. С какой скоростью должен двигаться автомобиль, чтобы пройти расстояние между этими городами в 5 раз быстрее? |
| Решение: | Пусть искомая скорость равна x км/ч. Тогда, согласно свойству пропорции, можем написать: |
| 50 / x = 1 / 5 | |
| Перемножим обе части уравнения на x ⋅ 5: | |
| 250 = x ⋅ 5 | |
| Решим уравнение: x = 50 ⋅ 5 = 250 (км/ч). |
Таким образом, чтобы пройти расстояние между этими городами в 5 раз быстрее, автомобиль должен двигаться со скоростью 250 км/ч.
Проверка корректности решения

После того, как вы решили задачу, очень важно проверить корректность своего решения. Для этого можно использовать несколько способов.
- Перечитайте условие задачи еще раз, чтобы убедиться, что вы правильно его поняли и учли все условия.
- Проверьте правильность вычислений. Отметьте достаточно времени для проверки, избегайте ошибок вида: опечатки, знаки умножения вместо знаков деления или наоборот.
- Проверьте правильность ответа на задачу. Следите за единицами измерения, если они есть в задаче.
Если вы нашли ошибки в своем решении, попробуйте еще раз решить задачу, чтобы исправить ошибку. Если ошибок не нашли, затратьте еще некоторое время на проверку. Помните, что проверка решения по времени тратит меньше, чем перерешивание задачи.