Как правильно перевести условия задачи на математический язык: советы и примеры

Статья расскажет, как перевести условия задачи на математический язык. Вы узнаете, как правильно формулировать математические выражения и работы с формулами. Подробно описаны основные правила и примеры перевода задач на математический язык.

Один из главных навыков, необходимых для успешного решения математических задач, — это умение переводить условия задачи на язык математики. Не всегда это происходит легко и просто, иногда нужно правильно понять, как переводить товарищей и их задачи на математический язык. В этой статье мы рассмотрим подробное руководство по переводу условий задач на язык математики.

Особое внимание будет уделено тому, как правильно выбрать переменные, какие математические операции использовать, и как сделать определение переменных в вашем математическом решении. Кроме того, мы рассмотрим несколько примеров и пошагово разберем, как переводить условия задач на язык математики.

Грамотный перевод условия задачи на язык математики — это первый шаг к успешному ее решению. Следуйте нашим советам и не бойтесь трудностей, то, что казалось непонятным и сложным, станет понятным и простым!

Как перевести условия задач на язык математики: руководство

Перевод условий задач на язык математики – это не столь сложный процесс, как может показаться на первый взгляд. Однако, чтобы выполнить перевод правильно и точно, необходимо следовать определенным правилам. Данный гайд позволит вам избежать ошибок и в будущем успешно решать задачи на математику.

Шаг 1: Внимательно ознакомьтесь с условиями задачи на родном языке. Представьте себе, что вы повторяете задачу своим собеседником. Это поможет понять, какие математические понятия и операции необходимы для ее решения.

Шаг 2: Обратите внимание на ключевые слова, которые часто встречаются в условиях задач. Например, «больше», «меньше», «выше», «ниже», «сумма», «разность» и т.д. Они означают какие-то определенные операции в математике и помогут вам правильно перевести условия на язык математики.

Шаг 3: Используйте переменные для описания неизвестных величин. Например, «x» и «y» – это часто используемые переменные. Они помогают описать неизвестные величины и выразить математическое равенство или неравенство.

Шаг 4: Составьте математические формулы на основе промежуточных и главных выражений в задаче. Старайтесь использовать знаки математических операций, такие как «+»,»-«,»*»,»/»,»=»,»» в соответствии с тем, какое действие необходимо выполнить с данными.

Шаг 5: Проверьте, правильно ли написана формулировка задачи на языке математики. Выполните проверку на наличие неправильно переведенных слов и ошибок в описании операций. Если есть необходимость, проверьте свое решение и, при необходимости, исправьте.

Следуя этому руководству, вы сможете правильно и точно переводить условия задач на язык математики. Это значительно упростит вашу работу и позволит выполнять решение математических задач быстрее и эффективнее.

Видео по теме:

Основные термины и определения

Условие задачи – описание проблемной ситуации, которая требует решения в рамках математической задачи.

Переменная – символ, используемый для обозначения некоторого неизвестного значения в задаче.

Уравнение – математическое выражение, связывающее переменные и числа при помощи знаков операций (сложения, вычитания, умножения, деления) и знака равенства.

Система уравнений – набор уравнений, связывающих несколько переменных, которые необходимо решить одновременно.

График функции – графическое представление зависимости переменных в функции.

Производная функции – показатель изменения функции в каждой точке ее графика.

Интеграл функции – обратная операция производной, которая определяет площадь под графиком функции.

Значение функции – числовое значение, полученное в результате вычислений в функции с заданными аргументами.

Дискретная величина – величина, которая может принимать конечное или счетное множество значений.

Непрерывная величина – величина, значение которой может быть любым числом в определенном диапазоне.

Математическое ожидание – среднее арифметическое значение величин, умноженных на вероятность их появления.

Дисперсия – мера разброса значений величины относительно ее математического ожидания.

Статистика – наука, которая изучает методы сбора, обработки и анализа данных для принятия решений на основе информации.

Вероятность – числовая мера возможности появления определенного события.

Выборка – набор случайно выбранных элементов из генеральной совокупности с целью оценки свойств последней.

Генеральная совокупность – полный набор элементов, который изучается в статистическом исследовании.

Шаг 1: Чтение условий задачи

Первый и самый важный шаг при решении математической задачи — это тщательное чтение условий задачи. Цель этого шага — понять, что требуется найти в задаче и какие данные уже даны.

Очень важно читать задачу внимательно и не спешить к ее решению. Иногда нужно прочитать условие несколько раз, чтобы понять, что от вас требуется. Не стесняйтесь выписывать важную информацию на бумаге или в блокноте, чтобы не потерять ее.

Когда вы уже понимаете, что нужно найти в задаче, важно определить, какие данные уже даны. Сколько измеряемых величин вам известно? Какие ограничения предъявляются к этим измерениям? Эта информация позволит определить, какие формулы и методы можно применить для решения задачи.

Важно также обратить внимание на ключевые слова в условиях задачи, например, «если», «как», «задано», «имеется». Эти слова могут указывать на важные подробности, которые нужно учитывать при решении задачи.

Шаг 2: Выделение нужной информации

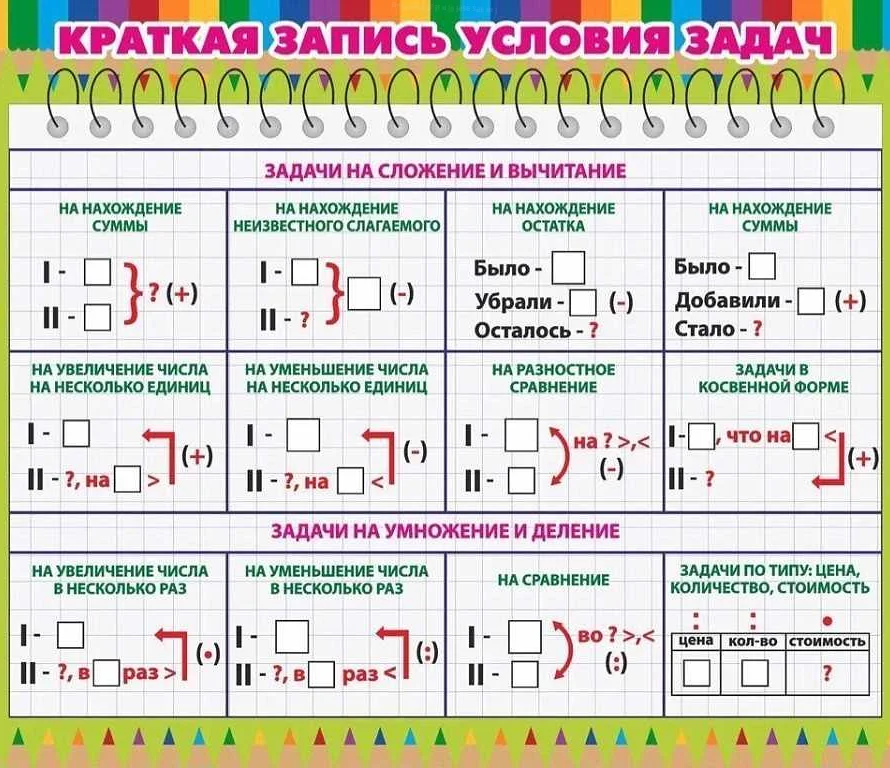
После того, как вы убедились, что понимаете условие задачи, нужно выделить все важные данные, которые понадобятся для ее решения. Перечислим, какие данные могут быть полезны:

• Количество объектов или предметов, о которых идет речь в задаче;
• Их свойства или характеристики (например, высота, вес, скорость);
• Количество людей или животных, участвующих в задаче;
• Длительность времени или расстояние;
• Цены, стоимости, скидки;
• Различные процентные ставки (например налоги, проценты);
• Другие важные данные, которые могут быть упомянуты в задаче.

Важно не упустить никаких деталей, потому что недостающая информация может стать причиной неправильного решения задачи.

Пример: Если мы решаем задачу на определение стоимости одного товара, нам необходимо знать общую стоимость всех товаров и количество товаров.

Количество товаровОбщая стоимость, руб

6

4500

Из этой информации мы можем выделить, что один товар стоит 750 рублей (4500 / 6).

Шаг 3: Формулировка математических условий

Формулировка математических условий – это ключевой шаг в решении математической задачи. На этом этапе необходимо перевести условия задачи на язык математики, используя известные математические символы и операции.

В начале этого шага важно определить все известные и неизвестные значения. Известные значения могут быть указаны явно в условии задачи, а неизвестные целесообразно обозначить переменными.

Затем необходимо проанализировать условие и сформулировать математическое уравнение или неравенство, которое позволит найти значение неизвестной величины. Математическое уравнение может включать в себя математические операции, такие как сложение, вычитание, умножение и деление.

Кроме того, важно учитывать единицы измерения и обозначения, используемые в условии задачи. Если значение неизвестной величины должно быть выражено в определенных единицах измерения, необходимо учесть соответствующие коэффициенты и факторы конвертации.

После того, как математические условия сформулированы, можно перейти к решению задачи, используя математические методы и инструменты.

Шаг 4: Составление уравнений и неравенств

После того, как мы более детально изучили условие задачи, можем перейти к составлению уравнений и неравенств. Этот шаг может быть довольно сложным, особенно если нет достаточного опыта в решении математических задач.

Во время составления уравнений и неравенств, мы должны учитывать все данные, представленные в условии. Мы должны попытаться сформулировать математическую модель задачи, которую мы будем использовать для ее решения.

Важно помнить, что всегда есть несколько способов составления уравнений и неравенств для одной и той же задачи. Нужно выбрать тот, который наиболее подходит для наших потребностей и умения в решении подобных проблем.

В результате составления уравнений и неравенств мы сможем перейти к следующему шагу, который заключается в решении полученной математической модели задачи.

Шаг 5: Приведение уравнений и неравенств к стандартному виду

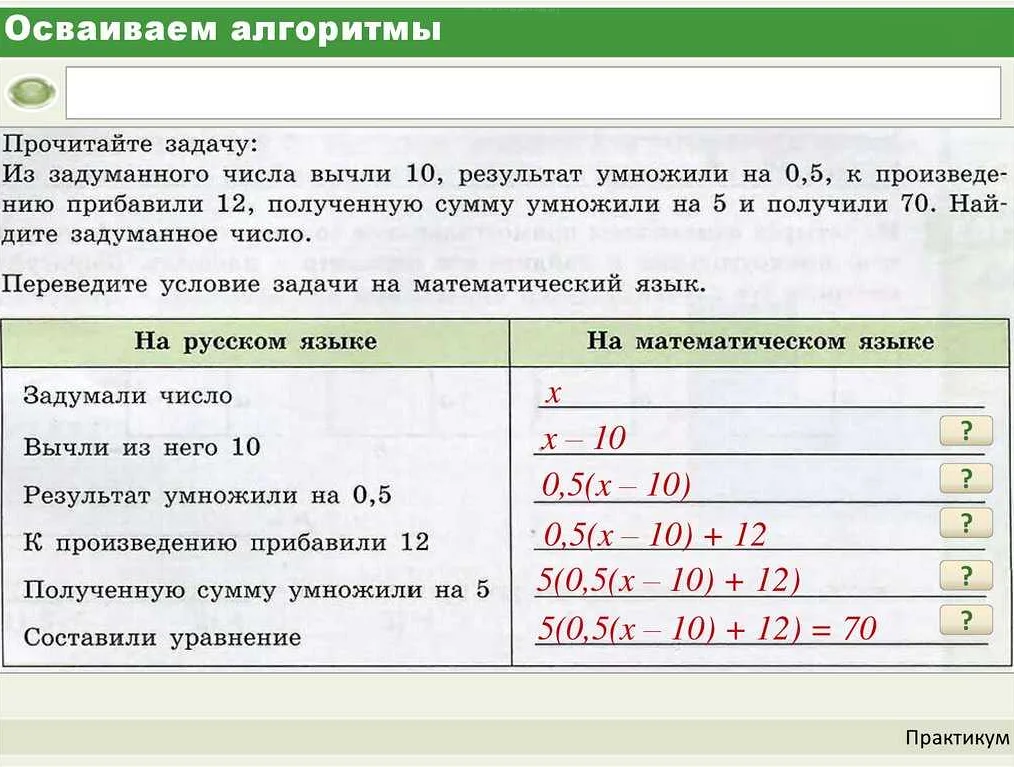
Важным этапом решения математических задач является приведение уравнений и неравенств к стандартному виду, который облегчает их дальнейшую обработку и решение. В стандартном виде уравнения и неравенства выглядят проще и привычнее, что облегчает восприятие задачи в целом.

Для приведения уравнений и неравенств к стандартному виду необходимо использовать определенные математические приемы, например, раскрытие скобок, объединение слагаемых, перенос элементов из одной части уравнения в другую и т.д. Каждый прием зависит от типа уравнения или неравенства и требует особого внимания со стороны решающего.

Иногда для приведения уравнений и неравенств к стандартному виду необходимо использовать дополнительные математические операции, например, взятие корня, возведение в квадрат и т.д. Однако необходимо помнить, что применение таких операций изменяет уравнение или неравенство, поэтому следует всегда проверять правильность применяемых действий и не допускать ошибок.

Поэтому важно не только знать математические приемы, но и уметь их правильно применять, чтобы получить правильное решение и верный ответ на задачу.

Шаг 6: Решение математической задачи

После того, как мы перевели условие задачи на язык математики и выразили все величины, необходимые для решения задачи, мы можем перейти к следующему шагу — решению задачи.

Для начала, нужно определить какие формулы и методы могут быть применены для ее решения. Здесь мы можем использовать базовые математические операции, такие как сложение, вычитание, умножение и деление, а также более сложные методы, такие как пропорции, преобразования уравнений и т.д.

Далее, нужно подставить известные значения в формулу и решить уравнение, чтобы найти неизвестное значение. В некоторых случаях может потребоваться выполнить несколько манипуляций с формулами для получения необходимого результата. Не стесняйтесь использовать калькулятор или инструменты компьютерной математики для выполнения более сложных вычислений.

Важно помнить, что ответ должен быть проверен на корректность и соответствие условию задачи. После этого можно сделать выводы о решении задачи.

Если решение задачи не подходит по каким-либо причинам, необходимо вернуться к предыдущим шагам и проверить правильность перевода условия на язык математики, выбор формул и методов.

Таким образом, последний шаг — решение математической задачи — позволяет сделать выводы о значении неизвестной величины на основе данных из условия задачи.

Особые случаи: задачи на проценты, вероятность и пропорции

Решение задач на проценты часто сводится к применению формулы:

Искомое значение = Исходное значение * (1 ± процентная ставка)

Если указано увеличение числа на определенный процент, то используется знак «+», а если уменьшение, то знак «-«. Важно также правильно определить, какую величину нужно найти и какую величину задавать как исходную.

Задачи на вероятность могут быть решены путем применения формулы:

Вероятность события = количество благоприятных исходов / количество всех возможных исходов

Важно учитывать все условия задачи, чтобы правильно подсчитать количество благоприятных исходов и общее количество возможных исходов. Также может потребоваться использование формулы суммы вероятностей для нескольких событий.

Задачи на пропорции требуют правильного сравнения двух величин. Для этого используется формула:

Отношение величин = большая величина / меньшая величина

Для решения задач на пропорции также могут потребоваться дополнительные условия, например, что сумма двух величин равна определенному числу или что одна из величин является процентом от другой.

Частые ошибки при переводе условий задач на язык математики

1. Неправильное определение переменных

Одна из частых ошибок при переводе условий задач на язык математики — это неправильное определение переменных. Некоторые слова могут иметь несколько значений, и в зависимости от контекста могут использоваться разные переменные. Поэтому необходимо внимательно проанализировать условие задачи и выбрать правильные переменные для каждого элемента.

2. Неправильно построенные выражения

Еще одна распространенная ошибка — неправильно построенные выражения. При переводе условий задач на язык математики, необходимо строго следовать математическим правилам и синтаксису. Некоторые слова или выражения могут привести к неправильному синтаксису, поэтому перевод нужно осуществлять с осторожностью.

3. Неверное понимание математических терминов

Некоторые математические термины могут иметь разные значения в разных областях математики. Неправильное понимание терминов может привести к неверному переводу условия задачи на язык математики. Поэтому перед переводом нужно убедиться, что вы понимаете термины с точки зрения математики, а не с вашей собственной интерпретации.

4. Отсутствие определенности

Иногда условия задач могут быть недостаточно четкими, что приводит к неточности в переводе на язык математики. Отсутствие ключевых слов или неопределенность в формулировке условия могут существенно затруднить перевод на язык математики. В этом случае обязательно нужно уточнить все непонятные моменты у автора задачи, чтобы правильно сформулировать условие.

5. Ошибки в расчетах

Наконец, при переводе условий задач на язык математики, не стоит забывать, что ошибка в расчетах может привести к неверному ответу. Поэтому, после перевода, обязательно нужно проверить правильность расчетов и тщательно анализировать каждый этап решения задачи.

Практика: примеры задач с решением

Пример 1

Одна коробка весит 12 кг. Сколько будет весить 5 таких коробок?

Решение

Для решения этой задачи нужно умножить вес одной коробки (12 кг) на количество коробок (5):

5 × 12 = 60

Ответ: 5 коробок будут весить 60 кг.

Пример 2

Дано 6 яблок. Сколько яблок останется, если отдать два яблока другу?

Решение

Для решения этой задачи нужно отнять количество яблок, которые отдают другу (2), от общего количества яблок (6):

6 — 2 = 4

Ответ: Останется 4 яблока.

Пример 3

Подсчитать сумму 5 последовательных натуральных чисел.

Решение

Сумма 5 последовательных натуральных чисел может быть найдена путем сложения чисел от 1 до 5:

1 + 2 + 3 + 4 + 5 = 15

Ответ: Сумма 5 последовательных натуральных чисел равна 15.

Пример 4

В прямоугольнике длиной 6 м и шириной 4 м необходимо выложить квадратные плитки со стороной 0,5 м. Сколько плиток требуется для этого?

Решение

Сначала нужно вычислить площадь прямоугольника, а затем разделить ее на площадь одной плитки:

Площадь прямоугольника = длина × ширина = 6 × 4 = 24 м²

Площадь плитки = сторона × сторона = 0,5 × 0,5 = 0,25 м²

Количество плиток = площадь прямоугольника / площадь плитки = 24 / 0,25 = 96

Ответ: Для выкладывания квадратных плиток со стороной 0,5 м требуется 96 плиток.

Итоги

Важность правильного перевода условий задачи: правильный перевод условий задачи на язык математики является фундаментом для корректного решения задачи. Даже небольшое недопонимание может привести к неправильному решению и потере баллов на экзамене или олимпиаде.

Основные приемы перевода: использование переменных, правильное расположение арифметических операций, перевод ключевых слов в математические термины. Кроме того, необходимо уметь интерпретировать математические символы и операции, используемые в условии задачи.

Примеры задач: были рассмотрены примеры задач разной сложности, и показано, как правильно переводить условия задач на язык математики. Отработаны навыки перевода словесных задач на язык математических формул.

Вывод: правильный перевод условий задач на язык математики является неотъемлемой частью решения многих задач. Следует уделять этому достаточно времени и внимания, чтобы минимизировать вероятность ошибок и повысить свои шансы на успех.

Вопрос-ответ:

Как перевести условие задачи с английского на язык математики?

Для перевода условия задачи с английского на язык математики необходимо уметь распознавать ключевые слова и фразы, связанные с математическими операциями (например, «плюс», «минус», «умножить», «разделить») и математическими понятиями (например, «число», «квадрат», «корень», «процент»). После распознавания слов и фраз следует составить математическое уравнение, отражающее условие задачи.

Есть ли какие-то правила для перевода условия задачи на язык математики?

Да, есть. Основное правило — переводить слова и фразы буквально, т. е. без истолкований и переносов значения. Также следует обращать внимание на порядок выполнения операций и определять неизвестные значения.

Какие ошибки чаще всего допускаются при переводе условия задачи на язык математики?

Ошибки могут быть различными, например, неправильный выбор математической операции, нарушение правил порядка выполнения операций, неправильное определение неизвестных значений и т. д. Ошибки также могут возникать из-за неудачного перевода ключевых слов и фраз. Важно внимательно читать и анализировать условие задачи и проверять свой перевод.

Какие инструменты помогают переводить условия задач на язык математики?

Существуют различные инструменты, которые могут помочь перевести условие задачи на язык математики. Например, программы-переводчики, которые могут распознавать математические операции и понятия. Также существуют онлайн-сервисы и технологии, которые позволяют составлять математические уравнения по условию задачи автоматически.

Должен ли я переводить условия задач на язык математики самостоятельно или могу использовать готовые переводы?

Желательно переводить условия задач на язык математики самостоятельно, чтобы лучше понимать суть задачи и корректно составлять математические уравнения. Однако, если вы затрудняетесь в переводе, можно воспользоваться готовыми переводами, но необходимо проверять их корректность.

Есть ли какие-то советы для того, чтобы правильно переводить условия задач на язык математики?

Да, советы могут быть следующими: внимательно читать условия задач, определять все ключевые слова и фразы, рассматривать порядок выполнения операций, не торопиться с переводом и проверять свой перевод. Также полезно ставить математические задачи с разными условиями и практиковаться в их переводе.

Может ли неправильный перевод условия задачи привести к неверному решению задачи?

Да, неправильный перевод условия задачи может привести к неверному решению задачи, так как неправильно составленное математическое уравнение не отражает сути задачи и может вести к неверным результатам. Поэтому важно внимательно и точно переводить условия задач на язык математики.