Как решить седьмое задание ЕГЭ по математике профиль: подробная инструкция

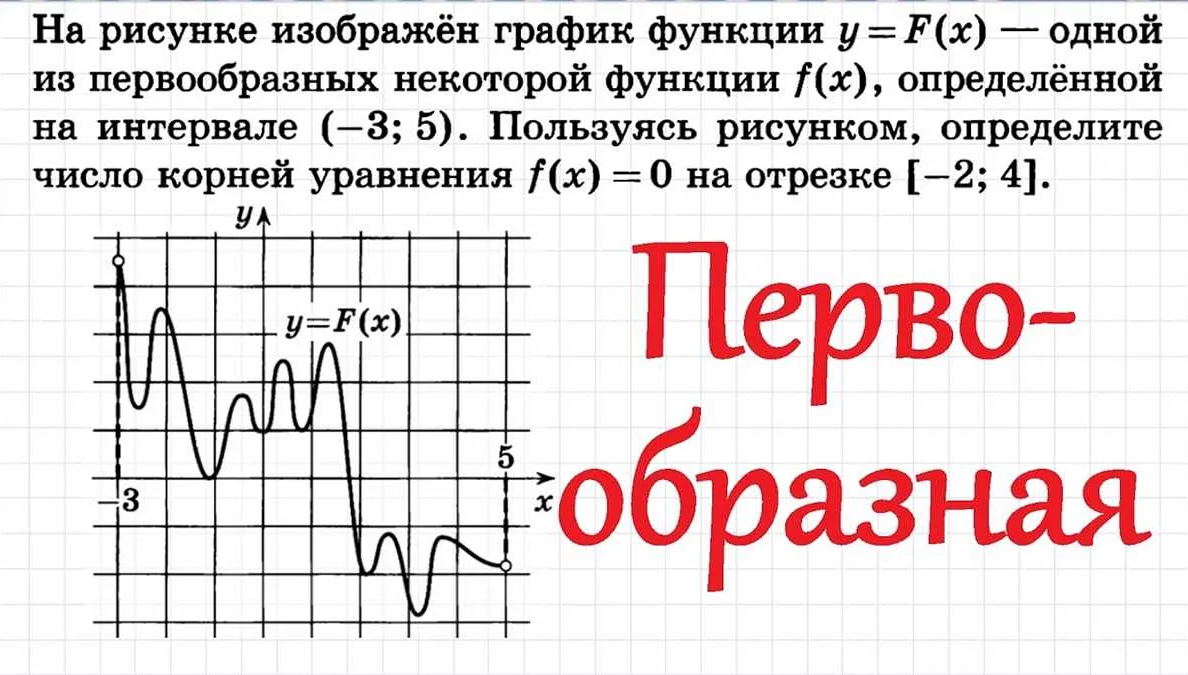
Узнайте, как успешно решать 7 задание по математике профильного уровня на ЕГЭ. В статье представлены полезные советы и рекомендации, которые помогут легко и быстро выполнить задание и получить высокий балл. Не бойтесь сложных формул и графиков, с нашими подсказками вы справитесь с экзаменом на отлично!

Все, кто готовится к сдаче ЕГЭ по математике профиль, знают, что 7 задание является одним из самых сложных на экзамене. Оно включает в себя задачу на нахождение экстремума функции. Для того, чтобы правильно выполнить эту задачу, необходимо твердо знать теорию и уметь применять её на практике.

В данном гайде мы рассмотрим подробно правильную стратегию решения задачи на нахождение экстремума функции. Опишем все шаги по порядку и предоставим несколько примеров для лучшего понимания.

Важно понимать, что экстремумы функций являются важным элементом в математике и многих других науках. Поэтому, правильное решение 7 задания на ЕГЭ может оказаться полезным в будущих исследованиях и работы по профилю.

Как решать 7 задание ЕГЭ по математике профиль: подробный гайд

7 задание ЕГЭ по математике профиль – это задача на составление уравнения. Чтобы успешно решить это задание, нужно иметь хорошее знание алгебры и уметь работать с координатами точек на координатной плоскости.

Первым шагом при решении этой задачи является выделение информации, которая дана в задании. Нужно внимательно прочитать условие и выделить все необходимые данные, такие как координаты точек, длины отрезков и другие характеристики фигур.

Далее необходимо определить тип геометрической фигуры, которую нужно описать уравнением. Например, это может быть прямая, окружность, парабола или гипербола.

После этого нужно воспользоваться знаниями алгебры и геометрии, чтобы составить уравнение искомой геометрической фигуры. В зависимости от типа фигуры, может потребоваться решить систему уравнений или использовать другие методы решения задач.

Напоследок необходимо проверить полученное уравнение и убедиться, что оно корректно описывает искомую геометрическую фигуру.

Решение 7 задания ЕГЭ по математике профиль требует хорошей подготовки и умения применять знания алгебры и геометрии на практике. Следуя рекомендациям в этом гайде, вы сможете успешно решить это задание и получить высокий балл на экзамене.

Видео по теме:

Понимание условия задачи

Понимание условия задачи является одним из самых важных аспектов при решении любой математической задачи. Некоторые задачи могут содержать скрытые детали или ограничения, которые могут повлиять на выбор используемого алгоритма или формулы.

Перед тем как начать решать задачу, необходимо внимательно прочитать условие и убедиться, что вы понимаете каждую часть. Если есть незнакомые термины или формулы, нужно изучить их и понять, как они связаны с решением задачи.

Кроме того, необходимо обращать внимание на заданные ограничения и условия. Они могут быть как количественными (например, «необходимо найти максимальное значение функции при условии, что x не может быть больше 5»), так и качественными (например, «необходимо разделить 12 яблок между 3 друзьями равномерно, но нельзя разрезать яблоки на части»).

Важно учитывать также более общие факты о задаче, такие как цель или контекст. Некоторые задачи могут иметь несколько подходов к решению, и выбор подходящего метода может зависеть от того, для чего решается задача или от ее смысла.

В целом, понимание условия задачи требует внимательности и тщательности. Если вы уверены, что понимаете условие, вы можете гораздо более эффективно выбирать методы и решать задачу.

Изучение предложенных формул

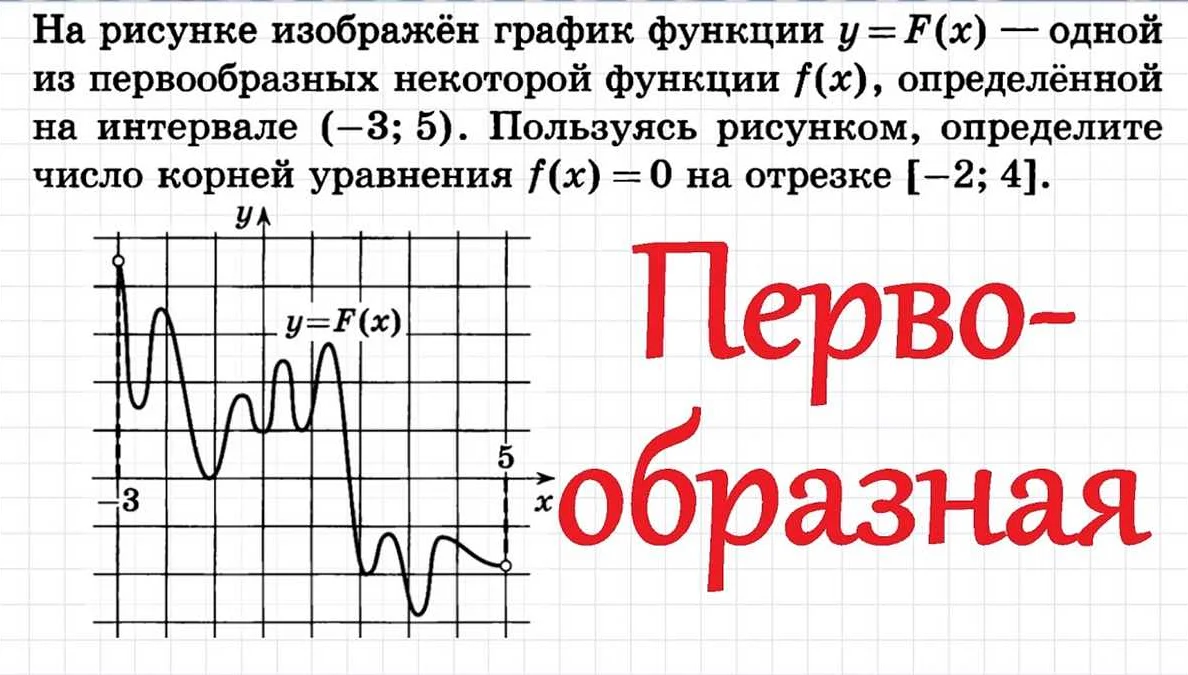
Одним из важных этапов подготовки к решению седьмой задачи ЕГЭ по математике является изучение предложенных формул. В ЕГЭ приведены несколько формул, которые необходимо знать и уметь применять.

В первую очередь, стоит изучить формулы для нахождения площади и периметра различных фигур. Это могут быть формулы для круга, треугольника, прямоугольника, трапеции и т.д. Кроме того, нужно знать формулу для объема и площади поверхности цилиндра, шара и конуса.

Важным моментом является знание формулы для решения квадратных уравнений. В седьмой задаче ЕГЭ нередко возникает необходимость решить квадратное уравнение. Для этого необходимо знать формулу дискриминанта и общую формулу решения квадратного уравнения.

Также стоит изучить формулу для нахождения среднего арифметического нескольких чисел. Эта формула может быть полезна при решении задач, связанных с нахождением средней оценки по нескольким предметам, или среднего возраста нескольких людей.

Важно не только знать формулы, но и уметь их применять. Поэтому рекомендуется не только выучить список формул, но и решать практические задания, чтобы закрепить их использование в практической деятельности.

Вопрос-ответ:

Какие методы можно использовать для решения 7 задания ЕГЭ по математике профиль?

Для решения этого задания можно использовать различные методы: метод разностей, метод наименьших квадратов, метод неопределенных коэффициентов, метод взвешивания уравнений. Каждый из них имеет свои преимущества и недостатки, поэтому перед началом решения задачи необходимо выбрать самый подходящий метод в зависимости от конкретной ситуации.

Как вычислить контрольную сумму в 7 задании ЕГЭ по математике профиль?

Для вычисления контрольной суммы в 7 задании следует сложить цифры полученного числа, начиная с последней. Если в результате получится число, состоящее из нескольких цифр, следует продолжить сложение, пока не останется одна цифра. Эта цифра и будет являться контрольной суммой.

Какие ошибки часто допускаются при решении 7 задания ЕГЭ по математике профиль?

Ошибки, которые часто допускаются при решении 7 задания, связаны с неправильным применением методов решения. Также может возникнуть ошибка при вычислении контрольной суммы. Для избежания ошибок необходимо тщательно проработать теоретическую часть и не спешить при выполнении задания.

Какие навыки необходимы для успешного решения 7 задания ЕГЭ по математике профиль?

Для успешного решения 7 задания необходимо умение применять различные методы решения, умение работать с большими числами и вычислять контрольную сумму. Также важно умение анализировать задание и выбирать наиболее подходящий метод решения.

Как правильно оформить решение 7 задания ЕГЭ по математике профиль?

Решение 7 задания следует оформлять в соответствии с требованиями ЕГЭ: указывать все промежуточные вычисления, необходимые для получения ответа, а также контрольную сумму. Также рекомендуется использовать разные способы решения и описывать их достоинства и недостатки.

Как выбрать самый подходящий метод решения для 7 задания ЕГЭ по математике профиль?

Для выбора подходящего метода решения необходимо внимательно прочитать задание и определить основные характеристики числа, которое необходимо найти. Затем следует оценить свои знания и умения в применении разных методов решения и выбрать тот, который больше всего подходит к данной задаче.

Какие материалы могут помочь при подготовке к решению 7 задания ЕГЭ по математике профиль?

Для подготовки к решению 7 задания можно использовать учебники по математике, задания и тесты для подготовки к ЕГЭ, а также видеоуроки и онлайн-курсы по математике. Также полезно заниматься самостоятельным решением задач и анализом своих ошибок.

Определение неизвестных величин

Определение неизвестных величин – это один из ключевых этапов решения задач по математике. Неизвестные величины – это те числа или величины, которые необходимо найти в результате решения задачи.

Прежде всего, необходимо внимательно прочитать условие задачи, чтобы выяснить, какие величины описываются, и определить, какие из них являются неизвестными.

Далее, можно использовать различные методы для определения неизвестных величин в зависимости от задачи. Например, для решения задач на пропорциональность можно использовать метод подобия фигур. Для алгебраических задач можно составлять уравнения и выполнять различные алгебраические операции.

Важно помнить, что в процессе определения неизвестных величин необходимо воспользоваться имеющимися в условии данными и ограничениями, чтобы избежать неверного результата. Также стоит проверять полученный ответ на соответствие смыслу задачи и ожиданиям.

Нахождение связей между величинами

Один из ключевых навыков, который требуется при решении седьмого задания ЕГЭ по математике, это умение находить связи между величинами. Очень часто в задании присутствуют несколько величин, и необходимо понять, как они зависят друг от друга.

Чтобы выявить связи между величинами, следует обратить внимание на их размерности и единицы измерения. Если две величины имеют одинаковую размерность и выражаются в одних и тех же единицах измерения, то можно предположить, что они имеют некоторую связь друг с другом.

Также необходимо обращать внимание на формулы, которые присутствуют в условии задачи. Если формулы содержат данные величины, то, вероятно, между ними есть какая-то связь.

Для того чтобы более наглядно представить связи между величинами, можно использовать таблицы, графики и диаграммы. Они позволят увидеть зависимость между величинами и лучше понимать условие задачи.

Наконец, стоит обратить внимание на смысловую нагрузку задачи и на область, к которой она относится (например, физика или экономика). Это позволит лучше понять, какие величины могут быть связаны друг с другом в данной ситуации.

Таким образом, нахождение связей между величинами является одним из важных компонентов при решении седьмого задания ЕГЭ по математике. Для этого следует обратить внимание на размерности и единицы измерения, формулы, использовать графики и таблицы, а также учитывать смысловую нагрузку задачи.

Поиск эквивалентных выражений

Эквивалентные выражения — это выражения, которые имеют одинаковое значение в любых условиях. В заданиях ЕГЭ это очень важно, поскольку они предлагают именно поиск таких выражений. Используя знание свойств алгебраических операций и законов математики, вы можете легко сделать задание.

Во-первых, следует запомнить свойства алгебраических операций. Например, вы можете использовать свойство дистрибутивности: a(b+c) = ab + ac. Это свойство очень полезно в задачах, где необходимо упростить сложные выражения. Также, не забывайте, что значения полученных выражений должны быть равными.

Во-вторых, помните о законах математики, таких как ассоциативность, коммутативность и др. Эти законы также могут помочь вам в поиске эквивалентных выражений.

Кроме того, следует использовать замены переменных и переводы с одной системы измерения в другую. Например, значение выражения в зависимости от одной переменной может быть эквивалентным значению другого выражения в зависимости от другой переменной. Также, перевод одной системы измерения в другую может помочь в заданиях, где нужно найти эквивалентные значения.

Чтобы проиллюстрировать это, рассмотрим следующее выражение: 2x + 4y — 5x + 2z. Используя закон коммутативности, мы можем переставить местами переменные и получить эквивалентное выражение: -3x + 4y + 2z.

Важно понимать, что нахождение эквивалентных выражений требует времени и практики. Но, если вы научитесь навыку поиска эквивалентных выражений, это значительно упростит решение задач ЕГЭ по математике профильной биологической направленности.

Подстановка конкретных значений в уравнения

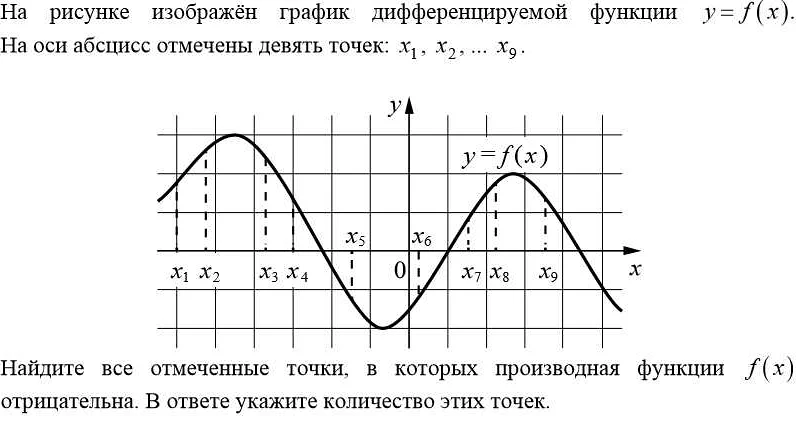
Одним из важных шагов при решении задач по математике является подстановка конкретных значений в уравнения. Это помогает проще понять условие задачи и применить соответствующую математическую формулу.

Например, в задаче на расчет периметра квадрата можно предположить, что его сторона равна 5. Затем подставить значение в формулу периметра P=4a, где a — сторона квадрата. Получим P=4*5=20.

Если задача будет формулироваться в виде уравнения, например, решить уравнение 3x+5=17, то конкретное значение можно найти, выразив x из уравнения. В данном случае x=(17-5)/3=4.

При решении задачи на нахождение значения функции можно также использовать подстановку конкретных значений. Например, если нужно найти значение функции y=2x-1 при x=3, то подставим значение x в формулу и получим y=2*3-1=5.

Подстановка конкретных значений в уравнения помогает не только найти решение задачи, но и проверить его правильность. После нахождения решения следует проверить его, подставив результат в исходное уравнение. Если обе части уравнения равны, то решение верное.

Решение уравнений и неравенств

Решение уравнений и неравенств — это важный шаг в разделе алгебры и может часто встречаться в заданиях ЕГЭ по математике. Основной принцип при решении уравнений и неравенств заключается в том, что обе стороны должны быть равны или одна должна быть больше или меньше другой. При этом необходимо правильно применять операции и свойства арифметики.

Кроме того, при решении неравенств необходимо учитывать знаки чисел и правильно определять, когда они изменяют свое значение. При решении уравнений существует несколько методов, включая подстановку, приведение подобных слагаемых и использование формулы дискриминанта.

Также при решении уравнений и неравенств необходимо учитывать условия задачи, которые могут повлиять на правильность ответа. Использование таблиц и графиков может помочь в наглядном представлении решения уравнений и неравенств.

• • При решении уравнений и неравенств необходимо:
    1. правильно применять операции и свойства арифметики;
    2. учитывать знаки чисел и условия задачи;
    3. использовать различные методы решения, включая подстановку, приведение подобных слагаемых и использование формулы дискриминанта.

Правильное решение уравнений и неравенств является неотъемлемой частью решения заданий ЕГЭ по математике и может повлиять на итоговую оценку. Поэтому важно уделить ему достаточно внимания и времени.

Проверка ответа на соответствие условию задачи

После того, как вы решили задачу, необходимо проверить правильность своего ответа. Для этого нужно внимательно прочитать условие задачи и удостовериться, что ответ соответствует ее требованиям.

В случае, если в условии задачи есть ограничения на значение переменных или определенные условия, например, «x должна быть больше нуля», необходимо убедиться, что решение удовлетворяет этим условиям. Если это не так, то ответ неверен.

Также важно проверить ответ на предмет правильного перевода единиц измерения, если они присутствуют в задаче. Например, если в задаче говорится о расстоянии в километрах, ответ должен быть дан также в километрах, а не в метрах.

При проверке ответа можно использовать таблицу значений, если она была построена в ходе решения. Если ответ таблицы совпадает с ответом задачи, значит, решение верное.

Наконец, можно проверить ответ, подставив его обратно в исходное уравнение или неравенство. Если полученное равенство или неравенство верны, значит, ответ корректный.

Проверка корректности вычислений

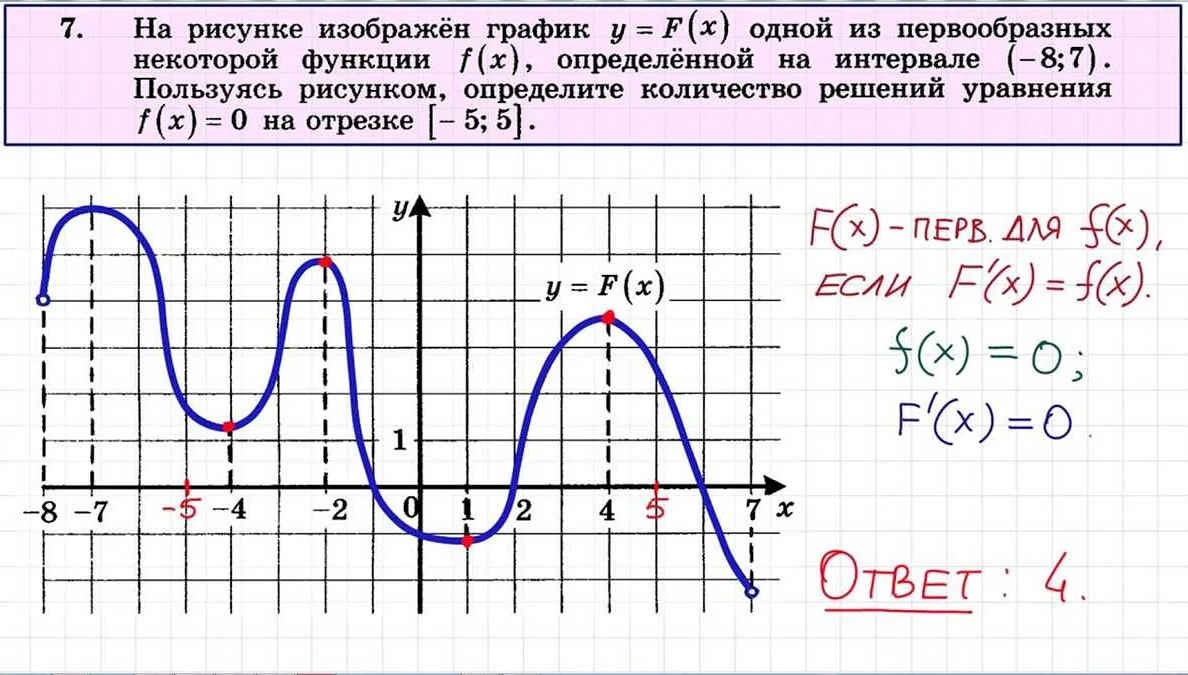
Когда вы решаете задания ЕГЭ по математике, особенно в профильной части, очень важно не только получить правильный ответ, но и проверить его корректность. Ведь одна ошибка может привести к неверному результату и потере баллов.

Первым шагом в проверке вычислений является повторение действий. Вычислите ответ еще раз, используя другой метод или проверочную формулу. Если вы получили тот же результат, значит, скорее всего, все верно.

Вторым шагом является анализ условия задачи. Проверьте, что вы правильно поняли условие и правильно выбрали математические операции. Например, если в задаче нужно найти скорость, то необходимо разделить пройденное расстояние на время, а не наоборот.

Третьим шагом является проверка промежуточных результатов. Если в задаче есть несколько действий, то необходимо проверить каждый из них. Если вы получили неверный промежуточный результат, то нужно найти ошибку в вычислениях и исправить ее.

• • • Не забывайте про порядок действий. В математике существует определенный порядок выполнения действий. Если вы используете скобки, то сначала нужно выполнить действия в скобках, а только потом — остальные действия.
    • Округление. Если в задаче требуется округлить ответ, то не забудьте, что не все числа округляются по правилам «большое к меньшему». Иногда требуется округление до определенного знака после запятой или до целого числа, а иногда нужно округлить до ближайшего четного числа.

Таким образом, для проверки корректности вычислений нужно повторять действия, анализировать условие задачи, проверять промежуточные результаты, не забывать про порядок действий и особенности округления. При этом стоит обращать внимание на каждую цифру и каждое действие, чтобы минимизировать ошибки.

Использование графических методов

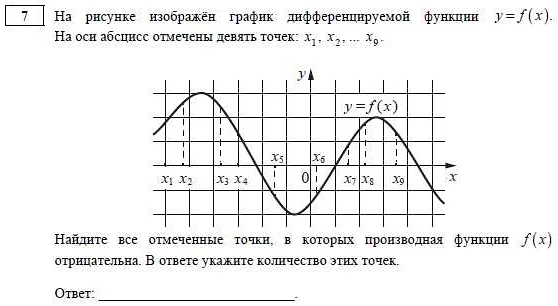
Графические методы могут быть очень полезны при решении математических задач, включая задания ЕГЭ. Например, использование графиков позволяет наглядно представлять функции и их свойства, что может помочь в поиске решения. Кроме того, графические методы, такие как построение графиков функций, могут помочь в проверке правильности ответа.

Одним из самых полезных графических методов является построение графика функции. Это позволяет увидеть форму функции, определить точки пересечения графиков, максимальные и минимальные значения функции и т.д. Если задание включает в себя график, то его необходимо анализировать и использовать для решения задачи.

Еще одним полезным графическим методом является использование координатной плоскости. Это позволяет наглядно представлять расположение точек и линий на плоскости и решать задачи, связанные с геометрией и алгеброй.

Важно помнить, что графические методы должны использоваться в сочетании с алгебраическими методами, а не в качестве их замены. Кроме того, необходимо уметь читать и анализировать графики функций, чтобы правильно использовать графические методы при решении задач.

• • • Полезные советы:
    • Внимательно читайте условие задачи и выделяйте ключевые слова.
    • Прорабатывайте графические методы на примерах и упражнениях.
    • Не забывайте, что графические методы должны использоваться в сочетании с алгебраическими методами.

Практика на примерах

На практике, чтобы решить задание 7 ЕГЭ по математике профиль, необходимо уметь правильно применять полученные знания на конкретных примерах. Для этого можно использовать различные источники, такие как учебники, задачники и онлайн курсы.

Например, вы можете попробовать решить задачи из официальных сборников ЕГЭ для подготовки к экзамену. Эти задачи являются наиболее подходящими для тренировки, так как они максимально приближены к тому, что вы встретите на экзамене.

Кроме того, на практике полезно использовать различные приёмы и стратегии для решения задач. Например, можно использовать метод перебора вариантов, применять формулы и методы изученных тем, а также делать схемы и рисунки для визуализации задачи.

• • • Также стоит обратить внимание на стратегию времени, когда решаете задачу. Не стоит тратить слишком много времени на одну задачу, если у вас на это недостаточно времени. Лучше перейти к следующей задаче и вернуться к той, которая вызвала затруднения, в конце.
    • Ещё одна полезная стратегия — проверка ответа. Важно проверять свои ответы до того, как перейдете к следующей задаче. Также не забудьте о том, что на экзамене можно проверить свои ответы несколько раз, поэтому стоит использовать эту возможность.
    • Наконец, рекомендуется решать экзаменационные задачи в том порядке, который вам удобен. Некоторые считают, что лучше начинать с самых простых задач, а затем переходить к более сложным, но это не всегда справедливо. Выбирайте стратегию, которая работает лучше для вас.