Огэ математика задачи про шины как решать

Учебное пособие по решению задач ОГЭ по математике на тему шины. Подробное объяснение решения задач, примеры и советы для успешной подготовки к экзамену.

Задачи по математике ОГЭ — это обязательная часть экзамена, и они могут быть различной сложности. Одной из типичных тем, которые могут встретиться в задачах, является шины. Решение задач на эту тему требует понимания основных понятий и формул, а также умения применять их на практике.

Перед тем как решать задачи, важно внимательно прочитать условие и выделить основные данные. Некоторые задачи про шины могут содержать информацию о диаметре, ширине, протекторе и других характеристиках шин. Далее необходимо разобраться, какие формулы и правила применимы к данной задаче.

Одна из ключевых формул, которую следует знать при решении задач про шины, — это формула для вычисления длины окружности. Она выглядит следующим образом: L = 2πr, где L — длина окружности, а r — радиус шины. Из этой формулы можно вывести другие формулы, например, для вычисления диаметра (D = 2r) или радиуса (r = D/2).

Важно помнить, что при решении задач по математике ОГЭ про шины необходимо быть внимательным к деталям и не забывать проверять свои вычисления. Если возникли затруднения, полезно использовать подсказки и шаблоны решения задач на эту тему, которые можно найти в учебниках или интернете.

Итак, чтобы успешно решать задачи по математике ОГЭ про шины, необходимо уметь анализировать условие задачи, применять соответствующие формулы и правила, а также проверять свои вычисления. Практика и знание основных понятий помогут вам стать уверенным в решении таких задач и достичь хороших результатов на экзамене.

Как решать задачи по математике ОГЭ про шины

Задачи по математике ОГЭ про шины могут быть сложными, но с правильным подходом и методикой их можно успешно решить. В этом разделе мы рассмотрим несколько шагов, которые помогут вам справиться с такими задачами.

1. Внимательно прочитайте условие задачи. Это может показаться очевидным, но очень важно внимательно прочитать условие задачи, чтобы понять, какие данные даны и какие величины нужно найти. Используйте подчеркивание или выделение ключевых слов, чтобы лучше запомнить их.

2. Постройте схему или рисунок. Во многих задачах про шины полезно нарисовать схему или рисунок, чтобы визуализировать ситуацию. Это поможет вам лучше понять, какие данные вам нужны и как их использовать.

3. Определите неизвестные величины. В задачах про шины часто нужно найти какую-то неизвестную величину, например, диаметр или радиус шины. Посмотрите, какие данные даны и какие величины нужно найти. Если возможно, обозначьте неизвестные величины буквами, чтобы вам было проще работать с ними.

4. Используйте подходящие формулы и свойства. Вам может потребоваться использовать формулы и свойства из геометрии или алгебры, чтобы решить задачу. Проверьте, какие формулы и свойства изучены вам на уроках и примените их соответствующим образом.

5. Решите уравнение или систему уравнений. Если задача требует решения уравнения или системы уравнений, приступите к их решению. Используйте изученные методы решения уравнений, такие как подстановка или выделение корней.

6. Проверьте свой ответ. После того, как вы получили ответ на задачу, проверьте его, подставив значения обратно в условие задачи. Это поможет вам убедиться, что ваш ответ верный.

Следуя этим шагам и уделяя достаточно времени на каждый из них, вы сможете успешно решать задачи по математике ОГЭ про шины и достигнуть хороших результатов на экзамене.

Понимание основных понятий

Для успешного решения задач по математике ОГЭ про шины необходимо хорошее понимание основных понятий. Рассмотрим некоторые из них:

• Радиус шины — это расстояние от центра шины до ее внешней поверхности. Обозначается буквой R.
• Диаметр шины — это расстояние между двумя точками на внешней поверхности шины, проходящими через ее центр. Обозначается буквой D.
• Периметр шины — это длина окружности, образующей внешнюю поверхность шины. Обозначается буквой P.
• Площадь поверхности шины — это площадь внешней поверхности шины. Обозначается буквой S.

Понимание этих понятий позволит вам правильно формулировать и решать задачи, связанные с шинами. Кроме того, они помогут вам лучше понять свойства и характеристики шин.

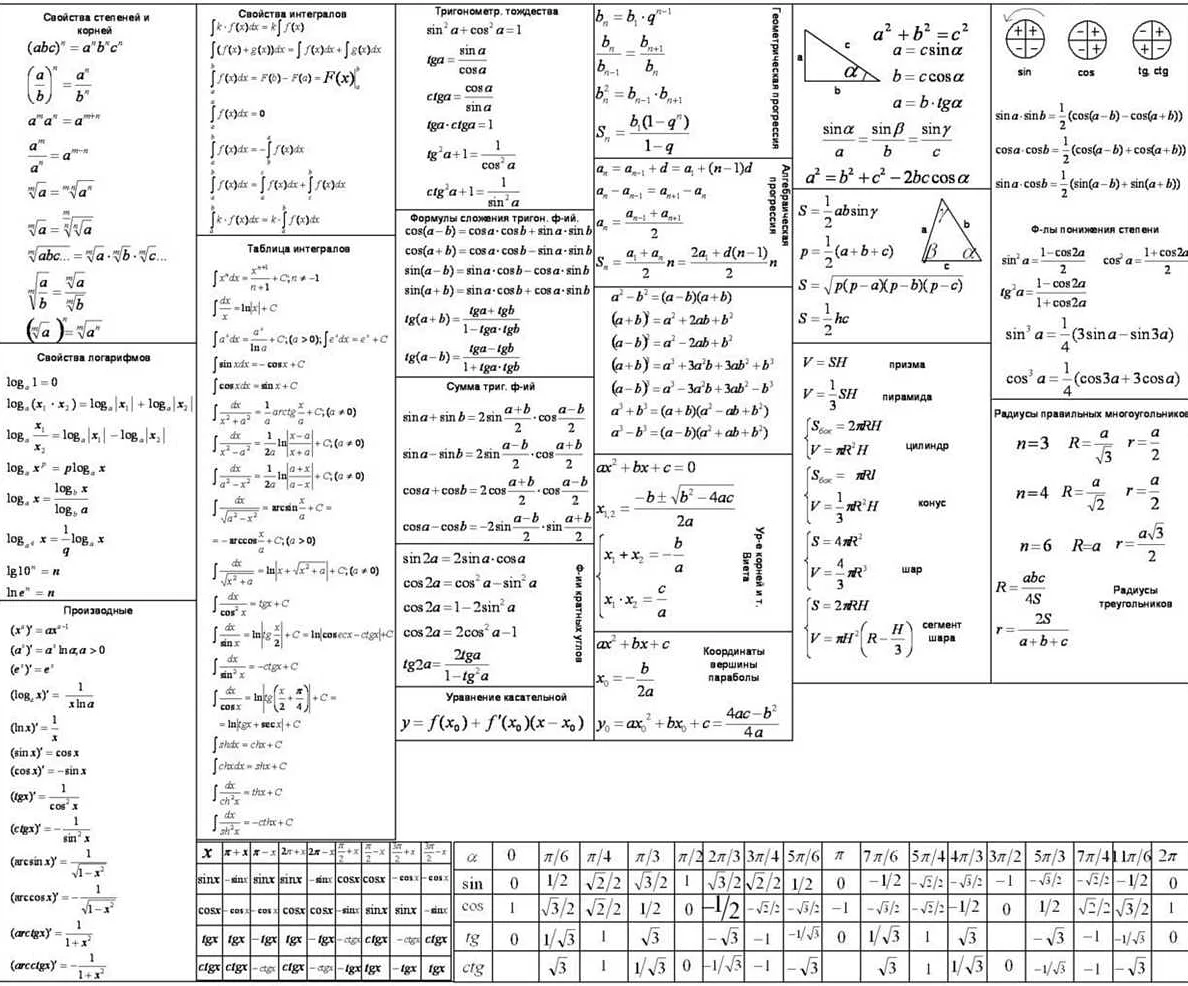
Знание формул и уравнений

Для успешного решения задач по математике на ОГЭ, необходимо хорошо знать основные формулы и уравнения, которые применяются в данной теме. Это позволит вам быстро и точно анализировать задачу и выбирать правильный подход к ее решению.

В задачах по шинам на ОГЭ часто используются следующие формулы:

1. Скорость — это отношение пройденного пути к затраченному времени: V = S / t, где V — скорость, S — пройденное расстояние, t — время, потраченное на преодоление данного расстояния.

2. Ускорение — это отношение изменения скорости к изменению времени: a = ΔV / Δt, где a — ускорение, ΔV — изменение скорости, Δt — изменение времени.

3. Средняя скорость — это отношение общего пройденного пути к общему затраченному времени: Vср = Sобщ / tобщ, где Vср — средняя скорость, Sобщ — общее пройденное расстояние, tобщ — общее время.

4. Работа — это произведение силы, действующей на тело, на путь, по которому она приложена: А = F * S, где А — работа, F — сила, S — путь.

5. Мощность — это отношение работы к времени, за которое она выполнена: P = A / t, где P — мощность, A — работа, t — время.

6. Закон сохранения энергии — энергия не может появиться из ничего и не может исчезнуть, она может только переходить из одной формы в другую: Ek + Ep = const, где Ek — кинетическая энергия, Ep — потенциальная энергия.

Знание данных формул и уравнений позволит вам более уверенно и эффективно решать задачи на ОГЭ по шинам, а также ускорит процесс решения.

Работа с геометрическими фигурами

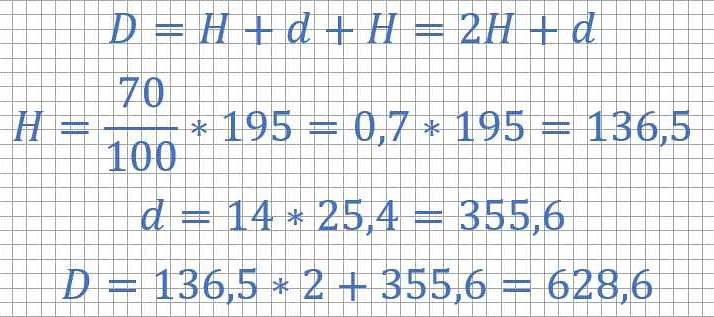
Решение задач по математике ОГЭ, связанных с геометрическими фигурами, требует от ученика умения анализировать и применять основные свойства фигур, а также применять соответствующие формулы и теоремы.

Перед тем как приступить к решению задачи, важно внимательно прочитать условие и проанализировать информацию о заданной фигуре. Затем нужно определить, какие известные данные можно использовать для решения задачи. Обратите внимание на ключевые слова и фразы, которые могут помочь вам выбрать правильную стратегию решения.

Для работы с геометрическими фигурами полезно знать основные свойства и формулы, такие как формула площади и периметра разных фигур, теоремы о сумме углов треугольника, параллельности прямых и другие. Необходимо также уметь применять эти знания в практике и применять их для решения конкретных задач.

Важно уметь рисовать схематические рисунки, чтобы проиллюстрировать свои рассуждения и лучше понять геометрическую ситуацию. Это поможет вам визуализировать задачу и легче найти решение. Используйте линейку и угольник для построения точных и четких рисунков.

При решении задач по геометрии не стесняйтесь использовать метод проб и ошибок. Если один подход не работает, попробуйте другой. Иногда задачи могут иметь нестандартное решение или требовать неожиданный подход к решению. Будьте творческими и ищите разные способы решения задачи.

Важно также проверить полученное решение и ответ на задачу. Перечитайте условие и убедитесь, что ваш ответ соответствует требованиям задачи. Проверьте расчеты и использованные формулы на возможные ошибки.

Решение задач по геометрии требует практики и упорства. Чем больше задач вы решите и чем больше вы будете практиковаться, тем лучше вы будете разбираться в геометрических фигурах и решать соответствующие задачи.

Использование пропорций и процентов

Проценты также часто встречаются в задачах про шины. Они используются для выражения отношения одной величины к другой в процентном выражении. Например, процент скидки или процент износа шин.

При решении задач с пропорциями и процентами, важно уметь правильно выразить отношения между величинами и правильно считать проценты. Для этого необходимо знать основные формулы и правила использования пропорций и процентов.

Пропорцию можно записать в виде: a/b = c/d, где a и b – известные величины, а c и d – неизвестные величины. Для решения пропорции необходимо найти значение одной из неизвестных величин.

Чтобы выразить процент одной величины относительно другой, используется формула: процент = (часть/целое) * 100%. Например, если шина износилась на 25%, это означает, что изначально осталось 75%.

Использование пропорций и процентов позволяет более удобно и точно решать задачи по математике ОГЭ про шины. Отработка навыков работы с пропорциями и процентами поможет вам успешно справляться с подобными заданиями и достигнуть хороших результатов на экзамене.

Анализ графиков и диаграмм

При анализе графиков следует обращать внимание на оси координат, шкалы и единицы измерения. Это поможет понять, какие значения представлены на графике и как они связаны между собой.

Для анализа графиков можно использовать различные методы. Например, можно определить точки перегиба и экстремумы, чтобы найти значения, при которых функция достигает максимального или минимального значения. Также полезно изучить форму графика или его направление, чтобы определить общую тенденцию изменения.

Диаграммы также могут быть полезны для анализа данных. Например, круговая диаграмма позволяет проанализировать состав целого и определить долю каждого компонента. Столбчатая диаграмма помогает сравнить значения различных категорий и найти тенденцию изменения.

При анализе графиков и диаграмм важно уметь читать и интерпретировать представленные данные. Это поможет в правильном решении задач по математике ОГЭ про шины и облегчит понимание материала.

Решение задач на скорость и расстояние

Для решения задач на скорость и расстояние важно знать основные формулы и уметь применять их в конкретных ситуациях. В данном разделе мы рассмотрим несколько типичных задач и покажем, как их решать.

Первый тип задач связан с расчетом времени, которое затрачивает автомобиль на проезд определенного расстояния с известной скоростью. Для этого воспользуемся формулой:

время = расстояние / скорость

Например, если автомобиль едет со скоростью 60 км/ч и нужно проехать расстояние 150 км, то время, которое затратит автомобиль на это, можно рассчитать следующим образом:

время = 150 км / 60 км/ч = 2.5 часа

Второй тип задач связан с расчетом расстояния, которое пройдет автомобиль за определенное время при известной скорости. Для этого воспользуемся формулой:

расстояние = скорость * время

Например, если автомобиль едет со скоростью 80 км/ч и движется в течение 3 часов, то расстояние, которое автомобиль пройдет за это время, можно рассчитать следующим образом:

расстояние = 80 км/ч * 3 часа = 240 км

Третий тип задач связан с расчетом скорости, при которой автомобиль проехал определенное расстояние за известное время. Для этого воспользуемся формулой:

скорость = расстояние / время

Например, если автомобиль проехал расстояние 400 км за 5 часов, то скорость, с которой он двигался, можно рассчитать следующим образом:

скорость = 400 км / 5 часов = 80 км/ч

Запомните эти формулы и умение применять их поможет вам успешно решать задачи на скорость и расстояние.

Применение алгоритмов и логики

Для успешного решения задач по математике ОГЭ про шины необходимо уметь применять алгоритмы и логику. Алгоритмы позволяют разбить сложную задачу на более простые шаги и последовательно их решить.

Первым шагом в решении задачи является внимательное прочтение условия. Необходимо понять, что именно требуется найти или решить. Затем необходимо проанализировать предоставленные данные и выделить самые важные из них.

Далее следует определить необходимые формулы и связи между величинами. Важно понимать, какие физические законы или математические формулы могут быть применены в данной задаче.

На основе полученных данных и формул можно составить план решения задачи. Разбить задачу на более простые шаги и определить последовательность их выполнения. Важно следовать этому плану и не пропускать какие-либо шаги.

При решении задач по шинам необходимо также уметь применять логические рассуждения. Здесь часто требуется провести анализ различных вариантов и их последствий. Например, при решении задачи о взаимосвязи скорости движения автобуса и времени в пути необходимо учитывать, как меняется расстояние, время и скорость в зависимости от заданных условий.

Важно помнить, что при решении задач по математике ОГЭ про шины ключевыми являются алгоритмы и логика. Они помогают систематизировать информацию, выявлять связи между величинами и проводить логические рассуждения. Такой подход позволит успешно решать задачи и достигать высоких результатов на экзамене.

Практика и повторение задач

Для успешного решения задач по математике ОГЭ про шины необходимо проводить регулярную практику и повторение уже решенных задач. Это поможет закрепить материал, развить навыки быстрого решения и уверенность в своих знаниях.

При решении задач рекомендуется следовать определенному алгоритму:

1. Внимательно прочитайте условие задачи и понимайте, что требуется от вас.
2. Выделите основные данные и величины, которые вам даны.
3. Составьте уравнение или систему уравнений, которые позволят решить задачу.
4. Решите полученное уравнение или систему уравнений и найдите ответ на задачу.
5. Проверьте полученный ответ и удостоверьтесь в его корректности.

Чтобы закрепить материал и развить навыки, рекомендуется регулярно решать задачи по шинам из предыдущих экзаменов, а также использовать учебники и дополнительные материалы с задачами на данную тему.

При решении задач можно использовать разные методы и подходы, поэтому рекомендуется изучить различные решения и подходы к задачам. Это поможет развить гибкость мышления и расширить набор инструментов для решения задач.

Не забывайте о регулярной практике и повторении уже решенных задач. Это поможет вам уверенно справляться с любыми задачами по математике ОГЭ про шины.

Видео по теме:

Какие основные шаги нужно выполнить при решении задачи по математике ОГЭ про шины?

Для решения задачи по математике ОГЭ про шины, следует выполнить следующие основные шаги: 1) Внимательно прочитать условие задачи; 2) Выделить ключевые данные и величины; 3) Составить и решить уравнение с использованием данных и известных величин; 4) Проверить полученное решение и ответ в условии задачи.

Как определить, какое количество шин нужно купить для замены старых, если известно, что автомобиль имеет n колес?

Для определения количества шин, необходимых для замены старых, можно использовать следующую формулу: количество шин = n / 2, где n — количество колес у автомобиля. Важно учесть, что автомобиль имеет четное количество колес, поэтому результат деления необходимо округлить в меньшую сторону.

Как найти суммарную стоимость покупки шин, если известна цена одной шины и количество шин?

Для определения суммарной стоимости покупки шин, необходимо умножить цену одной шины на количество шин. Формула для вычисления суммарной стоимости покупки шин выглядит следующим образом: суммарная стоимость = цена одной шины * количество шин.

Как определить, какое количество шин можно купить на заданную сумму, если известна цена одной шины?

Для определения количества шин, которое можно купить на заданную сумму, нужно разделить заданную сумму на цену одной шины. Формула для вычисления количества шин выглядит следующим образом: количество шин = заданная сумма / цена одной шины. Важно учесть, что результат деления нужно округлить в меньшую сторону.

Как определить, какую сумму нужно заплатить за n шин, если известна цена одной шины, а также известно, что при покупке m шин действует скидка?

Для определения суммы, которую нужно заплатить за n шин с учетом скидки, можно использовать следующую формулу: сумма = (n — m) * цена одной шины, где n — количество шин, m — количество шин, на которое действует скидка. Если никакая скидка не предусмотрена, то формула примет вид: сумма = n * цена одной шины.

Какой метод решения задачи про шины наиболее эффективен?

Эффективность метода решения задачи про шины зависит от конкретной задачи и уровня подготовки учащегося. Однако, в большинстве случаев рекомендуется использовать метод алгебраического решения задачи. Этот метод позволяет составить уравнение или систему уравнений, которые можно решить аналитически и получить точный ответ на вопрос задачи. В некоторых случаях также может быть полезно использовать графический метод решения задачи или метод последовательных приближений.