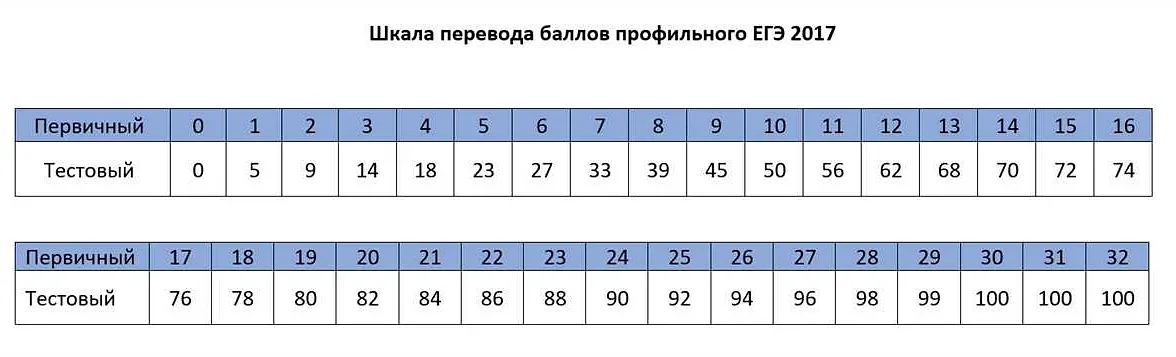
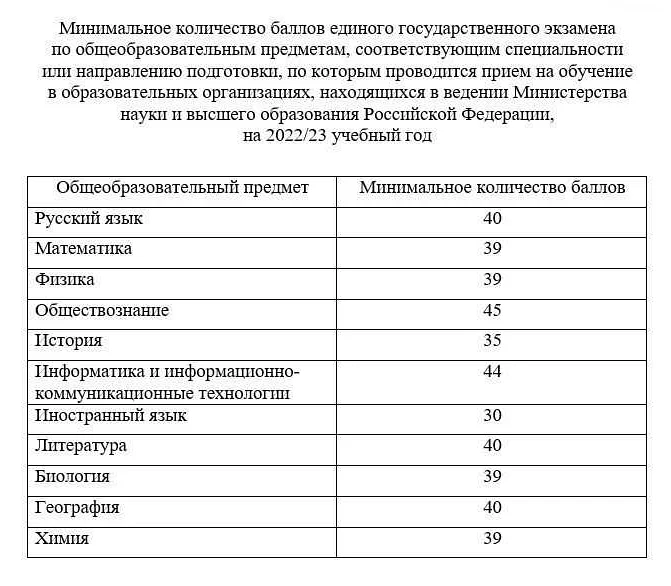
Как правильно оформить 13 задание в профильной математике: подробная инструкция

Узнайте, как правильно оформить 13 задание по профильной математике и получить максимальный балл на экзамене. В статье рассмотрены особенности задачи и подробное объяснение решения. Подготовьтесь к экзамену эффективно и успешно!

Решение 13-го задания по профильной математике может стать настоящей головной болью для большинства студентов. Оно требует не только знаний и умения применять математические формулы, но и логики и тщательной работы со всеми условиями задачи.

В данной статье мы представим вам подробный гайд, как правильно решить 13-е задание по профильной математике. Расскажем о особенностях задачи, дадим шаг за шагом инструкцию по ее решению и предоставим полезные советы, чтобы облегчить вам выполнение задания.

Решение 13-го задания по профильной математике может казаться сложным, но с нашим подробным гайдом вы сможете справиться с ним без проблем.

Как решить 13-е задание по профильной математике

13-е задание по профильной математике может показаться сложным на первый взгляд, но с правильным подходом можно быстро и легко решить эту задачу.

Первым шагом является внимательное прочтение условия задачи. Необходимо понять, какие данные нам даны и что именно требуется найти. Обратите внимание на каждую деталь, они могут быть ключевыми для решения задачи.

Далее, следует построить математическую модель, которая поможет решить задачу. Вы можете использовать формулы и принципы, изученные на уроках, чтобы составить такую модель. При этом не забывайте про соотношение между данными и тем, что требуется найти.

Когда математическая модель построена, необходимо решить уравнения и получить ответ на задачу. Важно не ошибаться в расчетах, поэтому старайтесь следовать поэтапно и проверять каждое действие.

Не забывайте проверить ваш ответ на корректность и соответствие условию задачи. Если вы допустили ошибку в расчетах, то лучше вернуться к этапу построения математической модели и перепроверить все действия.

Следуя этим шагам, вы сможете успешно решить 13-е задание по профильной математике. Не забывайте, что практика делает мастера, поэтому старайтесь решать как можно больше математических задач, чтобы улучшить свои навыки и успех в школе или на экзаменах.

Видео по теме:

Секреты успешного решения 13-го задания

1. Внимательно прочитайте условие задачи

Перед тем, как приступить к решению задачи, вам необходимо внимательно прочитать ее условие. Изучите все данные, которые даны в условии, и определите, какие из них необходимы для решения задачи. Это поможет вам составить правильный план решения и избежать ошибок.

2. Составьте план решения задачи

Прежде чем приступать к самому решению задачи, составьте план действий. Определите, какой метод решения задачи будет наиболее эффективным, и разбейте задачу на несколько подзадач. Это поможет вам не запутаться и решить задачу правильно.

3. Используйте все необходимые формулы и определения

13-е задание требует хорошего знания математических формул и определений. Применяйте их на практике, чтобы решить задачу. Если вы не уверены в своих знаниях, проконсультируйтесь со своим учителем или обратитесь за помощью к соответствующим учебникам и ресурсам.

4. Не забывайте про проверку ответа

После того, как вы закончите решать задачу, не забудьте проверить свой ответ. Снова прочитайте условие задачи, проверьте правильность применения формул и убедитесь в правильности полученного результата.

5. Практикуйтесь регулярно

Чтобы справляться с 13-м заданием и другими математическими задачами, необходимо практиковаться регулярно. Решайте разные задачи, изучайте новые формулы и определения, и тренируйте свой ум.

Понимание условия задачи на примере

Часто задачи по математике содержат много информации, которую нужно разобрать и понять, чтобы правильно решить ее. В этом нам может помочь пример.

Допустим, мы решаем задачу: «Тренажерная площадка предлагает своим клиентам абонементы на месяц, полгода и год. Стоимость абонемента на месяц составляет 2000 рублей, на полгода — 9000 рублей, а на год — 16000 рублей. Если клиент планирует посещать площадку 2 раза в неделю, какой абонемент выгоднее для него?»

Чтобы понять задачу, нужно разобраться, что такое абонемент и сколько раз в неделю хочет посещать площадку клиент. Из условия мы узнаем, что есть абонементы на месяц, полгода и год, и их стоимость. Наиболее выгодный для клиента будет абонемент, при котором общая стоимость за посещение площадки будет минимальной.

Используя информацию из условия, мы можем расчитать стоимость посещения для каждого из абонементов: для месячного — 8 000 рублей, для полугодового — 4 500 рублей, и для годового — 3 077 рублей. На основе этих данных можно сделать вывод, что выгоднее всего купить годовой абонемент.

Таким образом, пример помогает разобраться в задаче, выделить ключевую информацию и понять как ее использовать для решения задачи.

Анализ типичных ошибок

Решая 13-е задание по профильной математике, можно столкнуться с определенными ошибками. Ниже мы рассмотрим наиболее распространенные из них.

1. Неопределенность вида 0/0

При решении задачи может возникнуть неопределенность вида 0/0, которую сложно преобразовать. Чтобы избежать такой ситуации, рекомендуется внимательно проверять условия задачи и использовать все имеющиеся формулы.

2. Неправильный выбор способа решения

Для решения 13-го задания по профильной математике есть несколько способов, и неправильный выбор может привести к ошибке. Чтобы избежать этого, необходимо знать все возможные методы решения и выбирать тот, который подходит к данной задаче.

3. Несоблюдение правил алгоритма решения

Алгоритм решения 13-го задания по профильной математике необходимо строго соблюдать, и нарушение его правил может привести к ошибке. Рекомендуется внимательно читать условие задачи, следовать по шагам и проверять каждый результат перед переходом к следующему шагу.

4. Ошибки в расчетах и невнимательность

При решении 13-го задания по профильной математике следует быть крайне внимательным и не допускать ошибок в расчетах. Один пропущенный знак может привести к неверному ответу. Рекомендуется проверять результаты каждого действия и использовать калькулятор в случае необходимости.

Помните, что ошибки в решении 13-го задания по профильной математике могут привести к неверному ответу и уменьшению баллов на экзамене. Поэтому следуйте правилам решения и будьте крайне внимательными.

Выбор метода решения — подходы и рекомендации

При решении 13-го задания по профильной математике необходимо выбрать подходящий метод решения. Для этого следует тщательно изучить условие задачи, выделить важные данные и привести их в математическую форму. Только после этого можно переходить к выбору метода решения.

Один из основных подходов — использование формул и теорем. Если задача имеет математическую формулировку, необходимо проверить, есть ли для нее соответствующая формула или теорема. Если есть, то применение их может значительно ускорить решение.

Еще один подход — метод проб и ошибок. Для этого следует попробовать решить задачу разными способами и выбрать наиболее эффективный. Однако этот метод может занять много времени, поэтому следует использовать его только в крайних случаях.

Также можно использовать метод сравнения. Если задача связана с размерами, количеством или изменением какого-то параметра, можно сравнить его с другими известными и провести аналогию. Этот метод полезен в тех случаях, когда формулы и теоремы не подходят для решения задачи.

Важно помнить, что выбор подхода зависит от условий задачи и индивидуальных навыков и предпочтений каждого ученика. Поэтому рекомендуется практиковаться в решении разнообразных задач и выбирать оптимальный метод решения для каждой из них.

Использование графиков для упрощения решения

Графики могут быть полезным инструментом для упрощения решения математических задач. Они могут помочь визуализировать данные и облегчить анализ. В частности, графики могут быть использованы для решения задач на прямую и обратную пропорциональность, неравенства и многое другое.

При решении задач с помощью графиков, необходимо понимать, как выбирать точки для построения графика и как интерпретировать результаты. Один из способов выбора точек — использование таблицы значений. Для простоты рассмотрим задачу на прямую пропорциональность.

Пример: Найти формулу прямой, проходящей через точки (2, 4) и (4, 8).

Для решения этой задачи, нужно построить график с этими точками. Затем, используя таблицу значений, можно определить, что коэффициент пропорциональности равен 2. Значит, формула прямой имеет вид y = 2x.

Но не всегда можно решить задачу с помощью точек. Иногда приходится использовать другие способы. Например, при решении задач на неравенства, можно построить график неравенства и определить значимую область. Если решение не является явным, можно использовать метод проб и ошибок, подставляя значения и определяя, допустимы ли они в условии неравенства.

Графики также могут быть полезны при решении задач на определение максимума и минимума. Нужно построить график функции и найти ее экстремумы.

Наконец, следует отметить, что использование графиков не всегда является необходимым или возможным при решении задач. Но они могут быть полезным инструментом для упрощения процесса решения и визуализации данных.

Описание основных шагов решения

1. Прочитайте условие задачи и определите, какие данные вам представлены.

2. По условию задачи определите, какой метод решения требуется применить.

3. Составьте математическую модель задачи, используя приведенные данные.

4. Проведите необходимые вычисления, используя математическую модель.

5. Проверьте полученный ответ и убедитесь в его правильности.

6. При необходимости, перепроверьте свои вычисления и вернитесь к шагу 3.

7. Представьте ответ в виде числа или формулы, которая выражает его математически.

8. Проверьте правильность оформления ответа в соответствии с условием задачи.

9. Оформите решение задачи в аккуратной и читаемой форме, подчеркивая ключевые шаги и результаты.

10. Проверьте решение на наличие ошибок и опечаток.

Запомните, что правильное решение задачи зависит от нескольких важных шагов, каждый из которых требует точности и внимательности.

Примеры решения конкретных задач

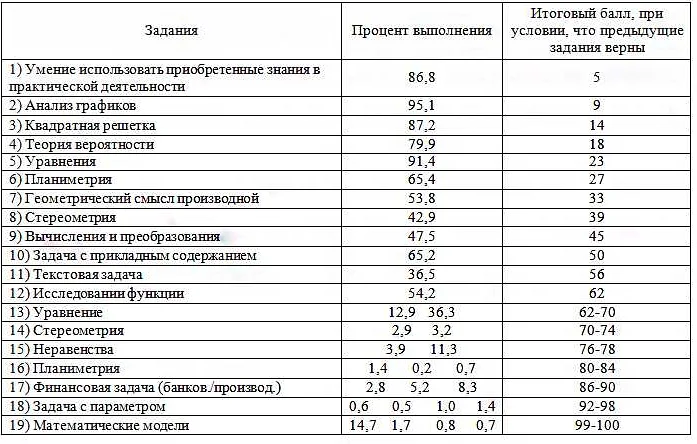
Задача 1. Найдите угол между диагоналями куба, если известен его объем.

Обозначим сторону куба через a. Тогда его объем будет равен V = a3.

Как известно, диагональ куба равна a√3. Таким образом, найдем значение диагоналей:

• Диагональ первой параллелепипедной грани равна a√2.
• Диагональ второй параллелепипедной грани равна a√2.
• Диагональ третьей параллелепипедной грани равна a√2.
• Диагональ первой поперечной грани равна a√3.
• Диагональ второй поперечной грани равна a√3.
• Диагональ третьей поперечной грани равна a√3.

Изобразим полученный куб:

	Диагонали поперечных граней
Диагонали параллелепипедных граней	a√2	a√2
	a√2	a√2
Диагонали поперечных граней		a√3

Займемся поиском угла между диагоналями. Для этого воспользуемся формулой косинусов:

cos(α) = (a√2)2 + (a√2)2 — (a√3)2 / 2(√2)2

cos(α) = 0.5

Таким образом, угол между диагоналями куба будет:

α = arccos(0.5) ≈ 60°

Обобщенный алгоритм решения

Задание 13 по профильной математике включает в себя решение нескольких задач с использованием систем неравенств и уравнений. Обобщенный алгоритм решения данных задач может быть разделен на несколько составляющих:

1. Определение переменных и запись уравнений;
2. Определение области значений переменных;
3. Решение системы уравнений и неравенств;
4. Проверка полученного решения на соответствие условиям задания и нахождение ответа.

Первый этап заключается в записи уравнений в соответствии с условиями задачи. Например, в том случае, если заданы два числа, их сумма их равна 10, то уравнение имеет вид: x + y = 10.

Далее следует определить область значений переменных, используя условия задачи. Например, если x — целое число от 0 до 5, а y — дробное число, большее 1, то можно определить области значений: 0 ≤ x ≤ 5 и y > 1.

Следующим шагом является решение системы уравнений и неравенств, которые были записаны на первом этапе. Это может быть сделано с помощью метода подбора, графического метода, метода коэффициентов и других методов.

Наконец, необходимо проверить полученное решение на соответствие условиям задания и определить ответ на задачу. Например, если условием задачи является поиск максимального значения x при удовлетворении системе уравнений и неравенств, то ответом будет максимальное значение x, которое нашлось в последнем этапе.

Рекомендации по тренировке навыков решения 13-го задания

Для того чтобы успешно решать задание №13 по профильной математике, необходимо усвоить основные понятия логики: логические выражения, тавтологии, противоречия, эквивалентные выражения и т.д.

Также важно разбираться в конструкциях «если-то» и «тогда-иначе», уметь работать с отрицанием и доказательством.

Чтобы тренировать свои навыки в решении задания №13, рекомендуется:

• Читать и понимать логические задачи и упражнения;
• Решать многочисленные примеры на логические выражения, используя таблицы истинности;
• Учиться проводить логические заключения и выводы на основе информации, содержащейся в условии задачи;
• Разбираться в различных логических конструкциях и их свойствах;
• Решать похожие задачи, чтобы облегчить процесс мышления при решении новых.

Помните, что все навыки приходят со стажем и требуют времени и терпения в упорядоченном развитии.

Если вы чувствуете, что на текущий момент не уверены в своих навыках решения задачи №13, не расстраивайтесь! Начните с простых задач и упражнений в логике, и тогда вы постепенно сможете улучшить свой уровень в решении сложных задач.

Возможные варианты усложнения задачи и их решение

1. Усложненный вариант задачи с добавлением еще одного поезда

В этом случае нам необходимо добавить еще один поезд в расписание и пересчитать минимальное время ожидания между отправлениями двух подряд идущих поездов. Для этого можно использовать аналогичные формулы и методы расчета, описанные выше.

2. Усложненный вариант задачи с учетом максимальной вместимости поезда

Если ограничить вместимость поезда, то расписание будет зависеть не только от времени отправления, но и от маршрута, наличия свободных мест и количества людей, которые должны поехать по данному маршруту. В этом случае можно использовать алгоритмы оптимального распределения пассажиров по поездам с учетом их вместительности и маршрута следования.

3. Усложненный вариант задачи с учетом погодных условий

При изменении погодных условий может измениться и время отправления поезда. Например, если по дороге будет сильный снегопад, то поезд может отправиться позже, чтобы увеличить безопасность передвижения. В этом случае можно использовать данные о погодных условиях и алгоритмы прогнозирования времени отправления и прибытия.

4. Усложненный вариант задачи с учетом времени на техническое обслуживание поезда

В реальной жизни поезда не всегда могут отправляться в срок из-за технических проблем или необходимости проведения профилактических работ. В этом случае можно использовать данные о времени на техническое обслуживание и алгоритмы оптимального управления расписанием.

Полезные источники для дополнительного изучения темы

Для более глубокого понимания материала, который подразумевается в 13-м задании по профильной математике, следует обратиться к следующим источникам:

• Учебники по теме — в них раскрыты основные теоретические положения и приведены различные методы решения задач. Для этой задачи рекомендуется ознакомиться со следующими учебниками: «Алгебра 10-11 класс» В. Г. Бевз, «Высшая математика за 24 часа» М.В. Иванов, «Алгебра. 10-11 класс» Д.В. Никольский.
• Онлайн-курсы — такие курсы доступны через Интернет и раскрывают материалы по всем разделам математики для разных уровней сложности. Например, на reshatel.pro можно найти онлайн-курсы по алгебре, геометрии, тригонометрии и другим разделам математики.
• Видеоуроки — обычно наглядным образом объясняются основные теоретические положения по теме, рассматриваются примеры решения задач. Советуем обратить внимание на видеоуроки математика В. Аргунова и Школа математики Фоксфорд.
• Практика решения задач — наиболее важный этап в изучении математики. На сайте math24.ru можно найти большое количество задач по алгебре, геометрии, тригонометрии, что позволяет не только закрепить знания, но и развивать навыки решения задач.

Вопрос-ответ:

Какие формулы надо запомнить для решения 13-го задания по профильной математике?

Перед началом решения задания стоит вспомнить формулы для расчета площадей и объемов, а также формулу Герона для вычисления площадей треугольников. Также пригодятся формулы тригонометрии для нахождения углов и сторон.

Можно ли использовать калькулятор при решении задания?

Обычно при решении заданий на профильной математике запрещается использование калькулятора. Однако, если в условиях задания это не указано, то можно воспользоваться калькулятором. В любом случае, рекомендуется доводить свойство умножить и разделить в уме до автоматизма, чтобы не тратить время на элементарные вычисления.

Как понять, какую формулу использовать для решения задания?

Чтобы правильно выбрать формулу для решения задания, нужно внимательно изучить условия задачи и определить известные и неизвестные величины. После этого выбирается нужная формула и подставляются известные величины. В некоторых заданиях может потребоваться несколько формул для решения, поэтому стоит внимательно читать задание перед выбором первой формулы.

Как ускорить решение задания?

Чтобы решить задание быстрее, стоит сначала рассмотреть более простые частные случаи, которые могут быть выведены из условия задания. Также можно использовать графический метод и нарисовать схему решения задания. Если задание просит найти численный ответ, то можно оценить его порядок величины перед решением, чтобы избежать дополнительных вычислений.

Как проверить верность решения задания?

Для проверки правильности решения задания можно воспользоваться методом обратной проверки, то есть подставить полученные ответы в уравнения условия и проверить, что они верны. Также можно перепроверить все расчеты и убедиться, что нет ошибок в вычислениях. Если есть возможность, то стоит сравнить свое решение с другими и убедиться, что результаты совпадают.

Как справиться с заданием, которое кажется сложным?

Если задание кажется сложным, стоит поделить его на более простые части и рассмотреть их по отдельности. Также можно использовать методы оценки и аппроксимации, чтобы примерно оценить ответ и ограничить его диапазон возможных значений. Не стоит отчаиваться и впадать в панику, лучше собраться и начать решать задание по шагам, перебирая различные варианты решения.

Как найти ошибку в решении задания?

Если в решении задания есть ошибка, стоит вернуться к началу и перепроверить все расчеты и формулы. Также можно попробовать перестроить решение задачи и рассматривать ее с другой стороны, чтобы найти ошибку. Если ошибка все еще не найдена, стоит обратиться за помощью к преподавателю или товарищу по учебе, который сможет подсказать точное место, где возникла ошибка.