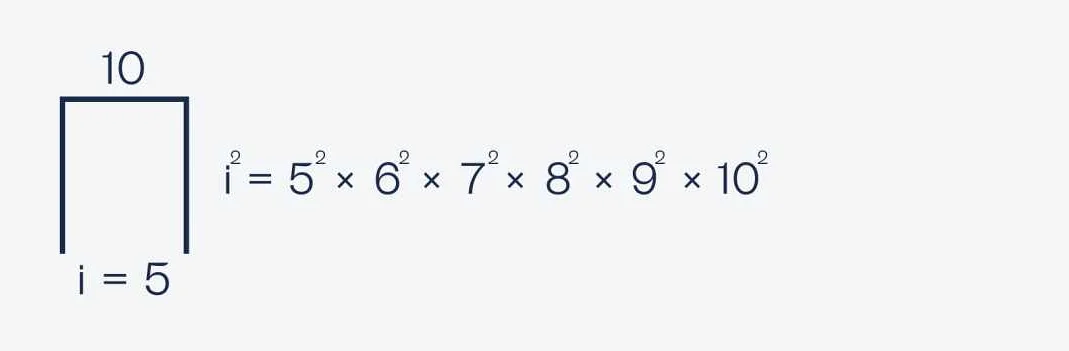Как правильно считать математическую сумму: простые правила и примеры

Узнайте, как правильно считать математические суммы и не допускать ошибок. Подробные объяснения простых и сложных примеров с пошаговыми инструкциями и примерами решения. Практические советы для упрощения расчетов и снижения вероятности ошибок.

Математические суммы являются основой многих математических задач и применений в реальной жизни. Однако, даже опытные математики могут иногда допустить ошибки при решении сложных задач. В этой статье мы рассмотрим полезные советы, которые помогут правильно считать математические суммы и избежать ошибок.

Первым и важным советом является правильное понимание терминов и обозначений. Некоторые обозначения могут быть запутывающими и вызвать путаницу при решении задач. Поэтому, перед тем как приступать к решению, необходимо внимательно изучить все обозначения и термины, связанные с задачей.

Кроме того, необходимо правильно организовать математические выражения и действия. Часто математические задачи содержат в себе множество операций и элементов, которые нужно правильно организовать и провести соответствующие действия. Важно не перепутать порядок действий и всегда следовать правилам и принципам математических операций.

В статье также будут представлены примеры решения различных математических задач, которые помогут читателю лучше понять и закрепить полученные знания и навыки в решении математических сумм. Надеемся, что эта статья будет полезной и поможет читателям успешно справляться с математическими задачами и суммами.

Значение математических сумм в жизни

Математические суммы играют важную роль в нашей жизни. Они помогают нам решать множество задач в различных областях, начиная от повседневных расчетов до научных и технических вычислений.

В повседневной жизни мы постоянно используем математические суммы для решения различных задач. Например, мы можем посчитать общую стоимость покупок в магазине или определить, сколько нужно выложить за чек в ресторане.

В научных и технических областях математические суммы также являются неотъемлемой частью их работы. Они помогают ученым и инженерам решать сложные задачи и создавать новые технологии.

Кроме того, умение считать математические суммы является важным навыком, который помогает в развитии аналитического, логического и критического мышления. Оно также может быть полезно в карьере, особенно в областях, связанных с наукой, технологией и экономикой.

Таким образом, понимание и умение считать математические суммы может иметь важное значение в нашей жизни, как на личном, так и на профессиональном уровне.

Основные правила работы с математическими суммами

Когда мы говорим о математических суммах, мы обычно имеем в виду суммирование ряда чисел. И чтобы грамотно считать математические суммы, нужно уметь следовать нескольким правилам. Следующие советы помогут вам справиться с этой задачей.

1. 1. Определите, как был задан ряд чисел. Прежде чем приступить к суммированию, нужно знать, как был задан ряд чисел. Это может быть арифметическая или геометрическая прогрессия, или же случайная последовательность чисел. Это поможет выбрать правильный метод суммирования.
   2. Используйте формулы для суммирования прогрессий. Если вы имеете дело с арифметической или геометрической прогрессией, то для суммирования можно использовать соответствующие формулы. Например, для суммирования арифметической прогрессии можно воспользоваться формулой суммы арифметической прогрессии:

S = (n/2)(a1 + an),

1. Учитывайте знаки чисел. Когда вы суммируете ряд чисел, нужно обратить внимание на знаки каждого числа. Некоторые числа могут быть отрицательными, что может привести к изменению знака общей суммы.
2. Следите за порядком суммирования. Когда вы суммируете ряд чисел, важно учитывать порядок суммирования. Например, при суммировании дробей, нужно умножать числитель первой дроби на знаменатель второй дроби и т.д.

Следуя этим простым правилам, вы сможете грамотно считать математические суммы, даже если ряд чисел является сложным или содержит отрицательные числа. Суммирование является важной задачей в математике и может применяться в различных областях, таких как финансы, наука и технологии.

Простые примеры суммирования

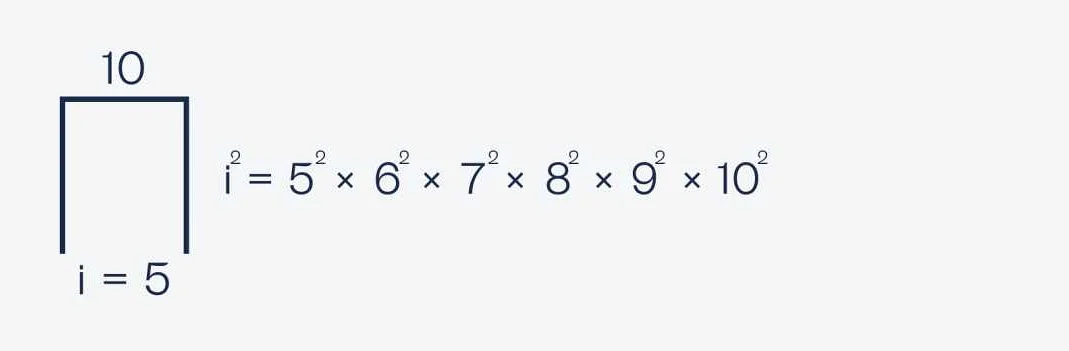
Прежде чем перейти к сложным математическим выражениям, давайте рассмотрим несколько простых примеров суммирования. Это поможет нам лучше понять основы и правила суммирования.

• Пример 1: Найдите сумму чисел от 1 до 5.
• Решение: Для нахождения суммы от 1 до 5, необходимо сложить все числа в этом диапазоне. То есть 1 + 2 + 3 + 4 + 5 = 15.

• Пример 2: Найдите сумму четных чисел от 2 до 10.
• Решение: Чтобы найти сумму четных чисел в заданном диапазоне, необходимо сложить все четные числа. В данном примере это: 2 + 4 + 6 + 8 + 10 = 30.

• Пример 3: Найдите сумму квадратов чисел от 1 до 3.
• Решение: Чтобы найти сумму квадратов чисел в заданном диапазоне, нужно возвести каждое число в квадрат, затем сложить полученные результаты. В данном случае, это будет: 1^2 + 2^2 + 3^2 = 14.

Эти простые примеры демонстрируют основы суммирования чисел. Они могут быть полезны для понимания более сложных математических операций.

Калькуляторы и программы для суммирования

Существует множество калькуляторов и программ, которые предназначены для упрощения работы с математическими суммами. Они могут быть как встроенными в операционную систему, так и скачиваемыми из интернета.

Один из самых распространённых калькуляторов, который входит во все операционные системы, – это Калькулятор Windows. В нём присутствуют функции для суммирования, вычитания, умножения и деления. Он также позволяет работать с процентами, вычислять квадратный корень и возведение в степень.

Если нужно произвести большое количество сложений и вычитаний, то можно воспользоваться специализированными программами. Например, программа MathCad предназначена для решения сложных математических задач, включая суммирование. Она позволяет выполнять операции как с числами, так и с переменными.

Если работать с большими объёмами данных, то удобно использовать электронные таблицы, такие как Excel или Google Sheets. Они предоставляют возможность вводить данные в таблицу, а затем производить необходимые операции, включая суммирование. При этом результаты автоматически обновляются при изменении входных данных.

В любом случае, выбор программы или калькулятора зависит от целей, которые нужно достичь, и объёма данных, с которыми необходимо работать.

Наиболее распространенные ошибки при суммировании

Суммирование – одна из самых базовых операций в математике, но при этом она может стать источником ошибок, которые могут сильно повлиять на результат расчетов. Рассмотрим наиболее распространенные ошибки при суммировании.

• Неправильное понимание синтаксиса – при суммировании необходимо правильно расставлять скобки, приоритеты операций, а также учитывать правила знаков. Так, умножение и деление выполняются до сложения и вычитания, и приоритет операций можно менять с помощью скобок.
• Неравномерный шаг – при суммировании суммы ряда обязательно нужно использовать равномерные шаги. Если шаг не равномерный, это может привести к ошибке в суммировании, особенно если ряд содержит большое количество слагаемых.
• Неучтенные элементы ряда – при суммировании нужно быть внимательным и учесть все элементы ряда. Например, если при суммировании ряда вы пропустили какую-то часть, то решение может быть неверным.
• Недостаточная точность – при суммировании нужно учитывать точность, особенно если ряд содержит большое количество слагаемых. Если вы устанавливаете недостаточную точность, то это может привести к существенным ошибкам в решении.

Избежать этих ошибок можно, если соблюдать правила математического синтаксиса, использовать равномерный шаг при суммировании, учитывать все элементы ряда и правильно устанавливать точность.

Обработка математических сумм в Excel

Microsoft Excel – это удобный инструмент, который в автоматическом режиме может выполнять сложные математические расчеты и суммирование значений. Рассмотрим, как обрабатывать математические суммы в Excel.

Сумма чисел в ячейках

Для суммирования значений в Excel необходимо выделить ячейки, которые нужно сложить, и затем кликнуть на кнопку суммирования, расположенную на верхней панели. Также можно использовать формулы, зависящие от типа данных, с которыми работает Excel.

Сумма ячеек с помощью функции SUM

Функция SUM используется для суммирования чисел в диапазоне ячеек или во всей таблице. Формула выглядит следующим образом: SUM(C2:C10), где C2:C10 – это диапазон ячеек, которые нужно сложить. Вычисление суммы можно автоматизировать, используя автозаполнение.

Сумма ячеек по условию с помощью функции SUMIF

Функция SUMIF используется для суммирования ячеек, удовлетворяющих определенному условию. Например, нужно посчитать сумму продаж конкретного товара. Формула выглядит так: SUMIF(A2:A10,»Товар1″,B2:B10), где A2:A10 – диапазон ячеек с наименованиями товаров, «Товар1» – условие, B2:B10 – диапазон ячеек с ценами на товар.

Сумма диапазона ячеек с помощью функции SUBTOTAL

Функция SUBTOTAL суммирует только видимые ячейки в диапазоне. Это очень удобно, когда при работе с большими таблицами нужно посчитать сумму только определенных строк или колонок. Формула выглядит так: SUBTOTAL(9, A2:A10), где 9 – функция суммирования, A2:A10 – диапазон ячеек, которые нужно сложить.

В заключение хочется отметить, что существует множество способов обработки математических сумм в Excel. Выберите тот, который наиболее удобен в работе с вашей конкретной таблицей и используйте его в своих проектах.

Различия между суммированием целых, дробных и отрицательных чисел

При суммировании целых чисел необходимо учитывать знак каждого слагаемого: если слагаемое положительное, то оно прибавляется к сумме, а если отрицательное, то вычитается из суммы. Например, сумма 3 + (-5) будет равна -2.

При суммировании дробных чисел также нужно учитывать их знаки. Важно общий знаменатель, чтобы слагаемые можно было складывать. Если знаменатели не совпадают, требуется их привести к общему знаменателю, а затем найти общий числитель. Например, сумма 1/5 + (-2/5) будет равна -1/5.

При суммировании отрицательных чисел можно сначала преобразовать их к положительным и затем сложить. Например, сумма -3 + (-2) можно записать как (-1)(3) + (-1)(2) = (-1)(3+2) = -5.

При суммировании различных типов чисел (между целыми, дробными и отрицательными) необходимо сначала преобразовать их к единому типу, чтобы их можно было складывать. Например, сумма 2 + (1/4) + (-3) может быть записана как 8/4 + 1/4 — 12/4 = -3.

• При суммировании целых чисел нужно учитывать знак каждого слагаемого
• При суммировании дробных чисел нужно учитывать их знаки и общий знаменатель
• При суммировании отрицательных чисел можно преобразовать их к положительным
• При суммировании различных типов чисел нужно привести их к единому типу

Задачи на суммирование в школьном курсе математики

В школьном курсе математики существует множество задач на суммирование, которые помогают студентам развить навыки работы с числами и научиться решать сложные математические задачи.

Одна из самых распространенных задач на суммирование — это подсчет суммы арифметической прогрессии. В такой задаче студенту нужно найти сумму всех чисел от начального до конечного. В школе студенты учатся находить суммы арифметических прогрессий, используя формулу: Sn=n(2a+(n-1)d)/2, где Sn — сумма прогрессии, n — количество элементов, а и d — начальный элемент и разность.

Еще одна популярная задача на суммирование — это нахождение суммы геометрической прогрессии. В такой задаче студенту нужно найти сумму всех членов геометрической прогрессии. Формула для нахождения суммы геометрической прогрессии выглядит следующим образом: S=a(1-q^n)/(1-q), где S — сумма прогрессии, a — первый элемент, q — интересующий нас множитель, а n — количество элементов.

Также существуют задачи на нахождение суммы ряда чисел разных порядков. В таких задачах студентам нужно научиться правильно раскладывать числовые ряды и уметь находить их суммы. Для решения таких задач необходимо уметь применять знания о числовых рядах и знаках суммирования.

В школьном курсе математики существуют различные задачи на суммирование, которые помогут вам развить умение работать с числами и научиться находить суммы разных прогрессий и рядов. Главное — понимать материал и уметь применять полученные знания на практике.

Сложение матриц и векторов

Сложение матриц — это одна из основных операций в алгебре. Для того чтобы сложить две матрицы, необходимо выполнить операцию с каждым элементом, находящимся на соответствующей позиции в каждой матрице. Результирующая матрица будет иметь такую же размерность, как и исходные матрицы.

Сложение векторов — это операция, при которой к каждому соответствующему элементу первого вектора добавляется соответствующий элемент второго вектора. Результатом является новый вектор, содержащий сумму элементов исходных векторов. Важно отметить, что при сложении векторов они должны иметь одинаковую длину.

Для удобства, сложение матриц и векторов можно представить в виде таблицы. Например, для сложения двух векторов a и b:

a = [3, 5, 2]

b = [1, 2, 3]

Координатаaba+b

1	3	1	4
2	5	2	7
3	2	3	5

Аналогично, для сложения матриц A и B:

A =

• [2 4 1]
• [3 5 2]

B =

• [1 3 3]
• [2 4 4]

ABA+B

1	2 4 1	1 3 3	3 7 4
2	3 5 2	2 4 4	5 9 6

Математические суммы в науке и технике

Математические суммы – это один из важнейших элементов математики, который применяется не только в науке, но и в технике. В науке суммы используются для описания различных закономерностей и моделей, которые помогают ученым понять многие явления в мире.

В технике суммы используются для решения разнообразных задач, например, оптимизация производственных процессов, расчеты электронных схем и многое другое. Неправильные расчеты могут привести к серьезным последствиям, поэтому правильное использование математических сумм является необходимым условием успешного выполнения технических задач.

Формулы сумм часто используются в механике и физике, например, для расчета скорости тела, энергии и т.д. В финансовой математике суммы используюся для расчета доходности инвестиционных портфелей. Без правильного использования суммы могут быть неверными, что может привести к ошибкам в решении задач.

• Пример: В формуле расчета доходности инвестиционного портфеля используется сумма всех инвестиций. Если инвестор не учитывает какую-то инвестицию, это может повлиять на общий расчет доходности портфеля.

Таким образом, понимание математических сумм является очень важным для решения задач в различных областях, где требуются точные расчеты и предсказания.

Вопрос-ответ:

Как правильно считать математические суммы?

Существует несколько методов для подсчета математических сумм, включая методы арифметических и геометрических прогрессий, методы интегралов и серий Тейлора, а также методы использования теории вероятностей и комбинаторики. При выборе метода считывания математических сумм необходимо учитывать сложность задачи, определяемой степенью сложности формулы и заданных данных, а также уровень математической подготовки исполнителя.

Как рассчитать сумму арифметической прогрессии?

Сумма арифметической прогрессии может быть рассчитана по формуле: S = (n/2)(2a + (n-1)d), где S — сумма, a — первый член прогрессии, d — разница между членами, n — количество членов. Например, для прогрессии 1, 3, 5, 7, 9 сумма будет равна 25.

Как рассчитать сумму геометрической прогрессии?

Сумма геометрической прогрессии может быть рассчитана по формуле: S = (a1(1-r^n))/(1-r), где S — сумма, a1 — первый член прогрессии, r — соотношение между членами, n — количество членов. Например, для прогрессии 1, 2, 4, 8, 16 сумма будет равна 31.

Как использовать интегралы для подсчета математических сумм?

Использование интегралов для подсчета математических сумм может быть полезным при решении задач высокой сложности, например, при расчете площади под кривой. Для этого необходимо преобразовать сумму в интеграл и применить методы интегрирования, например, метод замены переменных или интегрирование по частям. Однако, этот метод требует высокого уровня математической подготовки.

Как использовать теорию вероятности и комбинаторику для подсчета математических сумм?

Комбинаторика и теория вероятности могут быть использованы для подсчета математических сумм в задачах, связанных с числом сочетаний и перестановок, вероятностью событий и т.д. Например, для расчета числа сочетаний можно использовать формулу C(n,k) = n!/(k!(n-k)!), где n — количество элементов в множестве, k — количество выбранных элементов.

Как найти сумму бесконечного ряда?

Некоторые бесконечные ряды могут быть решены аналитически, используя методы анализа функций, теоремы о рядах и другие методы математического анализа. Однако, большинство бесконечных рядов требуют численного подсчета, который может быть выполнен, используя методы численного анализа, например, методы Монте-Карло или метод средних прямоугольников.

Как подсчитать сумму заданного ряда чисел в Excel?

Для подсчета суммы заданного ряда чисел в Excel необходимо использовать формулу SUM. Например, для расчета суммы чисел от A1 до A10, необходимо ввести в ячейку: =SUM(A1:A10).

Символьное суммирование и разложения

Символьное суммирование – это метод, в котором математическое выражение представляется как сумма функций. Такое представление часто используется для упрощения сложных формул и расчетов.

Символьное суммирование может быть реализовано с помощью специальных символов, таких как символ суммы. Он обозначается знаком «Σ» и позволяет записать сумму конечного или бесконечного числа слагаемых.

При символьном разложении выражения на несколько частей, мы можем применить формулы и правила сокращения, которые помогают упростить выражение. Например, если мы знаем формулу разложения произведения суммы двух чисел на слагаемые, мы можем применить ее, чтобы упростить сложное выражение.

Символьное суммирование и разложения используются во многих областях математики, физики, инженерных наук и иных научных дисциплинах. Они позволяют сократить количество вычислений и упростить сложные формулы.

• Примеры символьного суммирования:
  1. Сумма квадратов: Σn² = 1² + 2² + 3² + … + n²
  2. Формула Гаусса: 1 + 2 + 3 + … + n = (n * (n+1)) / 2

Правила символьного разложения:ПравилоПример

Произведение суммы на число	a * (b + c) = a * b + a * c
Разность квадратов	a² — b² = (a+b) * (a-b)
Сложение кубов	a³ + b³ = (a+b) * (a² — ab + b²)

Видео по теме: