Как правильно составить задачу по математике: советы и примеры

Полезные советы и инструкции по составлению задач по математике. Узнайте, как сделать свою задачу более интересной и подходящей для учеников всех уровней и возрастов.

Математика — это один из самых важных предметов в школьной программе. Сложность задач может варьироваться от простых уравнений до дифференциальных формул и интегралов. Однако, независимо от уровня сложности, задача учителя — не просто преподнести материал, но и научить учеников правильно составлять задачи. Это очень важный процесс, который помогает ученикам понимать материал и развивать логическое мышление.

Составление задач — это не только процесс придумывания математических примеров. Это искусство учителя, заключающееся в создании захватывающих, реалистичных и понятных задач, которые вызывают интерес у учеников. Хорошо составленная задача не только проверяет знания ученика, но и заставляет его думать, рассуждать и искать решение.

В этой статье мы расскажем о том, как правильно составлять задачи по математике. Вы узнаете о важности правильной формулировки задачи, о типах математических задач и о том, как их преподносить ученикам. Мы также предоставим некоторые примеры хорошо составленных задач, которые помогут вам лучше понять процесс составления задач.

Как составлять задачи по математике: советы и примеры

Составление задач по математике – это не только создание числовых примеров, но и умение поставить интересный вопрос и выбрать правильный уровень сложности. Ниже приводятся несколько советов для тех, кто хочет научиться составлять задачи по математике.

1. Определить цель

Прежде чем начинать создание задачи, необходимо определить ее цель. Это может быть демонстрация новой математической концепции, проверка знаний студентов, развитие художественного воображения и творческого мышления.

2. Выбрать подходящую тему

Тема задач должна соответствовать уровню знания и возрасту учеников. Выбирая тему, необходимо убедиться, что задача подходит для того уровня, на котором находятся ученики.

3. Использовать реальные примеры

Реальные примеры позволяют лучше понять и запомнить материал. Поэтому лучше использовать задачи, которые касаются повседневной жизни учеников.

4. Определить правильный уровень сложности

Необходимо определить правильный уровень сложности задачи. Если задача слишком легкая, ученики не будут заинтересованы. Если задача слишком сложная, ученики могут просто сдаться и потерять интерес к математике в целом.

5. Использовать различные типы задач

Чтобы задачи были интересными и разнообразными, нужно использовать различные типы задач: задачи на нахождение неизвестного, задачи на построение, задачи на сравнение, задачи на чтение графиков и т.д.

Следуя этим пяти советам, можно создать интересные и понятные задачи по математике, которые не только помогут ученикам понять новый материал, но и заинтересуют их.

Формулировка задачи: суть и примеры

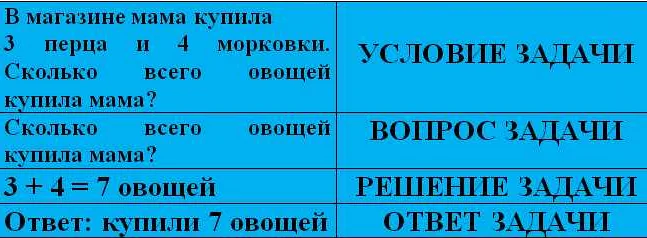
Одним из ключевых аспектов успешного решения математических задач является правильная формулировка самой задачи. Формулировка — это описание проблемы, которую необходимо решить, и определение того, что конкретно требуется найти в результате решения.

Хорошая формулировка задачи должна быть ясной, точной и содержательной. Она должна содержать все необходимые данные и условия, а также явно указывать на то, какой ответ также может быть полезен.

Примеры задач:

• Какова площадь квадрата, если известно, что его периметр равен 28 см?
• Сколько стоит 5 килограммов апельсинов, если 1 килограмм стоит 50 рублей?
• Для того, чтобы делить поле на две части, одну достаточно отгородить провелой-горизонтальной, а другую проволокой вертикальной, косо поставленной. Если проволока имеет длину 24а, то как надо выбрать ее расположение, чтобы оба куска поля были равными?

В каждой из этих задач формулировка включает все необходимые данные и условия, а также явно указывает на то, что требуется найти в результате решения. Таким образом, правильная формулировка задачи является важной составляющей ее решения.

Настройка ученика на математическую мысль

Правильная настройка ученика на математическую мысль – важный этап обучения, определяющий основу для дальнейшего успеха. В процессе изучения математики необходимо формировать у ученика соответствующие умения и навыки, а также внушать ему положительный настрой на эту наук.

Важным элементом настройки учащегося на математические задачи является понимание ключевых понятий и терминов. Объясните ученику что такое множество, функция, уравнение, график и другие математические термины, относящиеся к его уровню знаний. Также крайне важно помочь студенту сформировать понимание математических операций и связей между ними.

Далее рекомендуется научить ребенка четко думать и анализировать математические задачи. Сложные задачи нужно разбивать на части, чтобы легче было понимать, какие операции необходимо выполнить. Важно показать ученику, что каждая задача имеет свой подход и приложить усилия, чтобы научить его разбираться в нестандартных заданиях.

Наконец, важно помочь студенту развить его математическую интуицию. Решение задачи в большей части будет зависеть от его предзнания материала. Грамотное объяснение и правильно составленные упражнения помогут ученикам полностью погрузиться в математический мир и подготовиться к выполнению сложных заданий в будущем.

• Основные элементы настройки ученика на математическую мысль:
  1. Понимание ключевых терминов и понятий.
  2. Развитие умения анализировать задачи.
  3. Разработка математической интуиции.

Определение цели: какой знакомить ученика с материалом

Перед тем, как создавать задания по математике, необходимо определить цель знакомства ученика с материалом. Одним из важных моментов является понимание, какой уровень знаний и навыков уже имеет ученик.

Если ученик только начинает изучать определенную тему, то следует начинать с простых задач, которые помогут освоить основные понятия. Например, если ученик знакомится с геометрией, то можно предложить задания на построение простых фигур или определение их свойств.

Если же ученик уже имеет определенные знания, то цель может быть более сложной. Для таких учеников можно предложить задания с более сложными формулами или более глубокими математическими понятиями.

Однако, не стоит забывать о том, что каждый ученик уникален, и то, что для одного будет трудным заданием, для другого может быть достаточно легким. Поэтому, необходимо учитывать индивидуальные особенности каждого ученика при составлении заданий.

Выбор подходящих материалов для решения задач

Выбор подходящих материалов для решения задач играет важную роль в обучении математике. При правильном выборе материалов обучаемые овладевают необходимыми знаниями и навыками. Ошибки в выборе материалов могут привести к неэффективному обучению, а также к потере мотивации учащихся.

Как выбирать материалы для решения задач:

• Соответствие материалов уровню знаний учащихся;
• Применение различных типов задач: простых, средней сложности, сложных;
• Использование задач различной тематики для развития интереса учащихся к математике;
• Использование материалов с четкими пособиями и объяснениями;
• Выявление ошибок и допущенных учащимися опечаток.

Важно, чтобы материалы были легко доступны и удобны для использования как учителями, так и учениками. Адаптивные материалы, которые могут быть использованы в различных форматах и устройствах, также представляют собой важный критерий при выборе материалов. Также можно использовать интерактивные игры и задания, которые помогут ученикам лучше понять материал и повысить мотивацию к учебе.

Одним из важных критериев является достаточность и разнообразие задач. Слишком маленькое количество задач может не дать полного представления об умении учеников решать сложные задачи. Для создания успешной математической атмосферы учитель должен включать в уроки не только решение типовых задач, но и задач, развивающих логическое мышление и творческий потенциал.

Вывод: Правильный выбор материалов для решения задач является ключевым элементом обучения математике. Использование различных типов задач, разнообразие тематик, адаптивность и доступность материалов помогают обучаемым овладевать полным набором знаний, навыков и умений в математике. Качественные материалы способствуют повышению мотивации и интереса учеников к предмету.

Использование графических и текстовых подсказок

При создании задач по математике, кроме ясности и точности формулировок, важно также использовать графические и текстовые подсказки, которые помогут ученикам разобраться в условии задачи и выбрать правильный путь решения.

Графические подсказки могут быть представлены в виде схем, рисунков, графиков или таблиц. Например, если решается задача на построение графика функции, то его можно нарисовать на листе, указав оси координат, точки пересечения с осями и т.д. Это поможет ученикам визуально представить задачу и лучше понять, какие данные нужно использовать.

Текстовые подсказки могут быть представлены в виде ключевых слов или фраз, которые подчеркивают важность определенной информации. Например, если решается задача на расчет периметра треугольника, то в условии можно указать фразу «найдите сумму длин сторон треугольника» для того, чтобы правильно выделить необходимую информацию.

Также можно использовать списки с указанием порядка действий, которые нужно выполнить для решения задачи. Например, если решается задача на расчет площади круга, то можно указать следующие шаги: 1) найти радиус круга; 2) возведите радиус в квадрат; 3) умножьте результат на число Пи. Подобные списки помогут ученикам структурировать свои мысли и не пропустить важные детали при решении задачи.

Использование графических и текстовых подсказок упрощает процесс решения задач по математике и помогает ученикам получить лучшее понимание материала. Кроме того, это помогает повысить интерес и мотивацию учеников к изучению математики.

Деление задачи на несколько частей

Одним из важных принципов в составлении задач является их деление на несколько частей. Это позволяет сделать задачу более структурированной и понятной для ученика, а также помогает ему лучше понимать материал.

Первым шагом при делении задачи является формулировка вопроса. Например, «Сколько книг прочитал Максим на этой неделе?». Затем нужно определить необходимые данные. Например, сколько дней было на этой неделе и сколько книг Максим прочитал каждый день.

Следующим шагом будет разбиение задачи на части. Например, первая часть задачи может заключаться в том, чтобы вычислить количество дней на этой неделе, а вторая — определить, сколько книг прочитал Максим каждый день. Третья часть может заключаться в подсчете общего количества книг, которые Максим прочитал на этой неделе.

Каждая часть задачи может быть выделена в отдельный абзац или помечена номером. Это позволяет ученику проще ориентироваться в задаче и не пропустить ничего важного.

Оценка времени на решение задачи

Оценка времени на решение задачи является важным элементом успешного выполнения математических задач. От правильной оценки времени зависит не только качество ответа, но и скорость выполнения задания.

Важно учитывать уровень сложности задачи, количество данной информации и приведенных условий. Также необходимо учесть свой личный опыт решения подобных задач и уровень математической подготовки.

Нужно учитывать, что знание математических формул и алгоритмов необходимо для эффективного решения задач. Поэтому оценка времени на решение задачи должна включать в себя не только время самого решения, но и время на подготовку и изучение материала.

Изучив примеры и опыт других успешных решений, можно определить целесообразную стратегию для выполнения задачи: например, выбор оптимального решения по формуле или построения графиков. Еще одним полезным приемом является постановка задачи во время ночного сна, что часто ведет к неожиданным, но эффективным решениям.

Итак, предварительная оценка времени на решение задачи является ключевым элементом успеха в выполнении математических задач. Задача может занимать несколько минут или несколько часов — важно оценить время правильно.

Обеспечение возможности обратной связи

Важным аспектом при составлении задач по математике является возможность обратной связи для учеников.

Это может быть уточнение правильности ответа, пояснение решения, подсказка в случае затруднения или еще какой-либо комментарий от учителя.

Важно не только предоставить возможность задать вопрос или получить отклик на свой ответ, но и осуществлять это оперативно, чтобы ученики не теряли мотивацию и интерес к предмету.

Чтобы обеспечить максимальную эффективность обратной связи, можно использовать различные способы:

• создание электронных тестов, которые автоматически проверяются и выдают результат сразу же;
• организация общих консультаций после выполнения заданий;
• разработка заданий с пошаговым объяснением решения;
• индивидуальная работа с учениками, когда остается возможность уточнить каждый ответ.

Обеспечение возможности обратной связи при составлении задач по математике является необходимым условием для успешного обучения.

Мотивация ученика на решение задачи

Мотивация ученика на решение задачи играет очень важную роль. Если ученик видит цель и понимает, зачем ему нужно решить задачу, он будет к ней относиться более ответственно. Поэтому перед началом решения задачи необходимо объяснить ученикам, какая выгода ждет их после ее решения. Например, можно сказать, что правильное решение задачи поможет им лучше понять материал и подготовиться к экзамену.

Кроме того, важно создать интерес к задаче. Если ученик не видит в ней никакого интереса, то он будет решать ее просто из-за обязательства. Чтобы это не произошло, нужно показать, как задача связана с повседневной жизнью, какие ее приложения в реальном мире. Это поможет ученикам лучше увидеть ценность знаний, которые они получают, и захотеть решать задачи более осознанно.

Еще один метод мотивации учеников на решение задач – это дать им возможность решать интересные задачи. Решение избитых и однообразных задач может вызвать ученика чувство усталости и отвращения. В то же время, интересные задачи, которые требуют творчества и нестандартного подхода, вызовут больше интереса и восхищения. Они будут мотивировать учеников на поиск необычного решения и новых подходов к решению задач.

Таким образом, мотивация учеников на решение задачи является очень важным компонентом успешного процесса обучения математике. Мотивированные ученики будут стремиться к получению новых знаний, испытывать чувство удовлетворения от решения задачи и получать положительный опыт, которым можно поделиться с окружающими.

Видео по теме:

Вопрос-ответ:

Какие принципы необходимо учитывать при составлении задач по математике?

При составлении задач по математике необходимо учитывать не только образовательную ценность задачи, но и её практическую значимость для решения реальных проблем. Также важно учитывать возрастную категорию учащихся, чтобы задачи не были слишком простыми или, наоборот, слишком сложными для них.

Как сделать задачу более интересной и увлекательной для учащихся?

Чтобы задача была интересной и увлекательной для учащихся, её нужно связать с реальной жизнью, используя примеры из реального мира. Также можно добавить нестандартные условия, чтобы учащиеся не могли решить задачу, используя только стандартные алгоритмы и формулы.

Какое количество задач нужно давать на одно занятие?

Количество задач, которое нужно давать на одно занятие, зависит от сложности задач и уровня подготовки учащихся. В среднем, на одно занятие можно давать 5-7 задач, чтобы они успевали их решить и не уставали.

Какие типы задач по математике существуют?

Существует множество типов задач по математике, например: задачи на нахождение неизвестного числа (уравнения), задачи на нахождение площади и объема фигур, задачи на нахождение процента от числа, задачи на расчет времени и скорости и т.д.

Как использовать задачи с открытым ответом?

Задачи с открытым ответом полезны тем, что учащиеся могут показать свой творческий потенциал, а не ограничиваться стандартным ответом. Однако, чтобы использовать такие задачи, необходимо иметь возможность проверить ответ учащихся и оценить его корректность.

Каких ошибок нужно избегать при составлении задач по математике?

При составлении задач по математике нужно избегать использования сложных формул и условий, которые запутывают учащихся и усложняют задачу без необходимости. Также нужно избегать повторения уже известных учащимся задач, чтобы не утомлять их и не затягивать процесс решения.

Как оценивать решение задач учащихся?

Оценка решения задач учащихся должна быть объективной и основываться на правильности решения, а не на сложности задачи. Также нужно учитывать способ и скорость решения задачи, чтобы оценить не только результат, но и процесс решения.

Способы проверки решения задачи

Когда вы решаете математическую задачу, важно не только найти правильный ответ, но и убедиться, что он верный. Для этого существуют различные способы проверки решения.

Проверка в обратном порядке – один из самых простых способов проверки. Суть его заключается в том, чтобы использовать полученный ответ в обратной задаче и убедиться, что получим тот же результат. Например, если задача была на нахождение площади прямоугольника, то можно проверить свой ответ, найдя значение одной из сторон и сравнить результат с начальными данными.

Проверка с помощью аналогии – подходит для решения задач с похожими условиями. Для этого нужно найти аналогичную задачу, решить ее и сравнить результаты. Например, если задача была на нахождение длины окружности, то можно найти аналогичную задачу на нахождение площади круга, решить ее и сравнить полученные значения.

Проверка с помощью второго метода – используется для задач, которые можно решить несколькими способами. Для этого нужно выбрать другой метод решения задачи и сравнить результаты. Например, если задача на нахождение корней квадратного уравнения была решена с помощью формулы Дискриминанта, то можно использовать другую формулу и сравнить результаты.

Проверка решения задачи – важный этап в решении любой математической задачи. Она позволяет убедиться в правильности ответа и избежать ошибок. Выбирайте тот способ проверки, который наиболее удобен и соответствует условиям задачи.

Поощрение ученика: как усилить его успехи в математике

Математика может быть вызовом для многих учеников. Для того чтобы мотивировать их, необходимо уделить внимание следующим правилам:

• Привнести интерес: ученики, которые не видят в математике интереса, не будут стремиться изучать ее. Привнесите в уроки математики интерес с помощью задач, связанных с реальной жизнью, игр и головоломок.
• Наградить усилия: награда за усилия способствует мотивации учеников. Оцените учеников не только за результаты, но и за их усилия в учении, оцените их труд и терпение.
• Убедиться в успехе: помогите ученикам увидеть свой успех. Подтверждение того, что они делают, важно; подчеркивайте как они продвигаются в своем учении, даже если это малые шаги.
• Создать комфортную и безопасную обстановку: ученики должны чувствовать себя комфортно в классе. Они должны знать, что не только результаты важны, но и их чувства и мнение. Дайте им возможность высказываться, слушать, общаться, работать в группах.

Разработка убедительной стратегии поощрения учеников поможет им получить удовольствие от изучения математики и постоянно прогрессировать в ней.