Математика 6 класс как решать уравнения

Узнайте, как решать уравнения в математике 6 класса с помощью простых методов и правил. Научитесь упрощать уравнения и находить значение неизвестной переменной. Подробные объяснения и примеры помогут вам понять основы решения уравнений в 6 классе математики.

Решение уравнений — одно из важнейших навыков в математике. Умение правильно решать уравнения позволяет находить неизвестные значения и дает возможность решать самые разнообразные задачи. В шестом классе ученики начинают изучать основы алгебры и первые простые уравнения. На первый взгляд может показаться, что решение уравнений — сложный и запутанный процесс, но на самом деле все гораздо проще.

Первый шаг к решению уравнения — это понять его структуру и выделить неизвестную величину. Обычно неизвестная обозначается буквой, например, «х». Важно помнить, что уравнение представляет собой равенство двух выражений. Второй шаг — применить различные математические операции с целью избавиться от знаков и переместить все известные и неизвестные величины на одну сторону уравнения.

Важно помнить, что при применении операций к уравнению нужно сохранять равенство. Это означает, что то, что делается с одной стороной уравнения, должно делаться и с другой стороной.

Следующий шаг — решение полученного уравнения. Для этого необходимо выразить неизвестную величину через известные и рассчитать ее значение. Последний шаг — проверка полученного решения. Для этого заменяют найденное значение неизвестной величины в исходное уравнение и убеждаются, что оно верно. Если равенство сохраняется, то решение верно, если нет — необходимо повторить предыдущие шаги.

Решение уравнений может быть не только интересным, но и полезным умением, которое пригодится в жизни. Оно поможет решать задачи в финансах, физике, химии и других областях науки и техники. Важно развивать этот навык с самого раннего возраста, чтобы ученик мог успешно справляться с математическими задачами и достигать своих целей.

Шаги к решению уравнений в 6 классе

Вот простые шаги, которые помогут вам решить уравнения в 6 классе:

1. Изучите уравнение: внимательно прочитайте задачу и разберитесь, что она от вас требует. Определите неизвестную переменную, которую нужно найти.
2. Упростите уравнение: если уравнение содержит скобки или операции с числами, сначала выполните все эти действия. Упростите выражение, чтобы оно было более компактным и понятным.
3. Примените обратные операции: используйте обратные операции, чтобы избавиться от известных переменных и найти значение неизвестной переменной. Например, если уравнение содержит сложение, вычтите значение одной переменной из обеих сторон уравнения.
4. Проверьте свое решение: подставьте найденное значение переменной обратно в исходное уравнение и проверьте, что обе стороны равны. Если они совпадают, значит ваше решение верно.

Следуя этим шагам, вы сможете решать уравнения в 6 классе с легкостью. Постепенно, с практикой, ваш навык решения уравнений будет становиться все сильнее и вы сможете решать более сложные задачи.

Видео по теме:

Определение типа уравнения

Перед тем, как начать решать уравнение, необходимо определить его тип. Существуют различные типы уравнений, каждый из которых имеет свои особенности и правила решения.

Один из способов определить тип уравнения – это посмотреть на количество переменных в уравнении. Если уравнение содержит только одну переменную, то оно называется одномерным уравнением. Примеры одномерных уравнений: 3x + 2 = 8, 2x — 5 = 10.

Если уравнение содержит две переменные, то оно называется двумерным уравнением. Примеры двумерных уравнений: 2x + 3y = 10, x^2 + y^2 = 25.

Также существуют и другие типы уравнений, такие как системы уравнений, квадратные уравнения и т.д. Определение типа уравнения важно, так как для каждого типа уравнения существуют свои специальные методы решения.

Знакомство с базовыми математическими символами

Символы — это специальные знаки, которые обозначают определенные действия или элементы в математике. Вот некоторые из наиболее распространенных базовых математических символов:

1. Символ «+»

Символ «+» обозначает операцию сложения. Например, 2 + 3 = 5 означает, что если сложить число 2 и число 3, то получится число 5.

2. Символ «-«

Символ «-» обозначает операцию вычитания. Например, 5 — 3 = 2 означает, что если из числа 5 вычесть число 3, то получится число 2.

3. Символ «×»

Символ «×» обозначает операцию умножения. Например, 2 × 3 = 6 означает, что если умножить число 2 на число 3, то получится число 6.

4. Символ «÷»

Символ «÷» обозначает операцию деления. Например, 6 ÷ 3 = 2 означает, что если число 6 разделить на число 3, то получится число 2.

5. Символ «=»

Символ «=» используется для обозначения равенства. Например, 2 + 2 = 4 означает, что сумма чисел 2 и 2 равна числу 4.

Знакомство с базовыми математическими символами — это первый шаг к успешному решению уравнений. Они позволяют нам понимать и записывать математические задачи и операции правильно. Следующим шагом будет изучение правил использования этих символов в различных математических задачах.

Вопрос-ответ:

Как решать уравнения в 6 классе?

Для решения уравнений в 6 классе нужно следовать нескольким простым шагам. Сначала нужно записать уравнение, затем привести его к простейшему виду, избавиться от скобок и упростить выражение. Далее следует применить обратные операции для нахождения значения неизвестной переменной. Наконец, нужно проверить полученное решение, подставив его обратно в исходное уравнение.

Какие операции нужно применять для решения уравнений в 6 классе?

Для решения уравнений в 6 классе нужно знать основные операции сложения, вычитания, умножения и деления. Также необходимо уметь применять обратные операции, то есть противоположные к данным операциям. Например, если в уравнении присутствует сложение, то для его решения нужно применить вычитание.

Какой вид должны иметь уравнения в 6 классе?

Уравнения в 6 классе должны быть простыми и содержать только одну неизвестную переменную. Например, x + 5 = 10 или 2x = 12. Они также должны быть записаны в правильной математической форме, с правильным расположением знаков операций и скобок.

Как проверить правильность решения уравнения в 6 классе?

Для проверки правильности решения уравнения в 6 классе нужно подставить найденное значение переменной обратно в исходное уравнение и проверить, что обе его стороны равны. Если полученное равенство выполняется, то решение верно. Если же равенство не выполняется, то нужно перепроверить все шаги решения уравнения.

Какие ошибки чаще всего допускают ученики при решении уравнений в 6 классе?

При решении уравнений в 6 классе ученики часто допускают ошибки при выполнении арифметических операций, например, при сложении или вычитании. Они также могут забывать применить обратные операции или делают неправильные выводы на промежуточных шагах решения. Ошибки также могут возникать при приведении уравнения к простейшему виду или при проверке полученного решения.

Разбор простейшего типа уравнений

Простейший тип уравнений представляет собой уравнение вида ax = b, где a и b — известные числа, а x — неизвестное число, которое нужно найти.

Процесс решения простейшего уравнения включает следующие шаги:

1.	Перенесите число b на другую сторону равенства, меняя его знак.
2.	Разделите новое число слева на коэффициент a, чтобы найти значение x.

Например, для уравнения 2x = 8, мы переносим число 8 на другую сторону равенства и меняем его знак: 2x = -8. Затем делим -8 на 2, чтобы найти значение x: x = -4.

Таким образом, решение простейшего типа уравнений может быть достигнуто, следуя этим простым шагам. Этот метод позволяет ученикам разобраться с уравнениями и научиться находить их решения.

Использование операций для решения уравнений

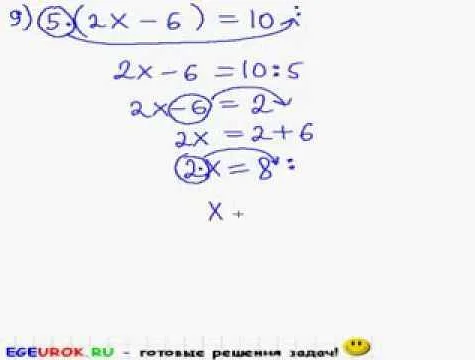
Для решения уравнений в 6 классе математики необходимо использовать различные операции: сложение, вычитание, умножение и деление. Зная правила этих операций, вы сможете легко решать простые уравнения и получать правильные ответы.

Первым шагом при решении уравнения является выделение неизвестного значения, которое обычно обозначается буквой. Например, в уравнении «2x + 5 = 15» неизвестное значение обозначено буквой «x».

Далее, используя операции сложения и вычитания, необходимо перенести все известные значения на одну сторону уравнения, а неизвестное значение на другую сторону. Например, чтобы решить уравнение «2x + 5 = 15», нужно вычесть 5 с обеих сторон уравнения: «2x = 10».

Затем, при помощи операции деления, можно найти значение неизвестного. В данном случае, нужно разделить обе части уравнения на 2: «x = 5».

Таким образом, значение неизвестной переменной равно 5, исходное уравнение «2x + 5 = 15» решено.

Важно помнить, что при использовании операций для решения уравнений необходимо выполнять одни и те же операции с обеими сторонами уравнения, чтобы сохранить его равенство. Если, например, вы добавляете число к одной стороне, нужно добавить его и к другой стороне.

Использование операций для решения уравнений может быть простым и эффективным способом получить правильный ответ. Поэтому, при выполнении математических задач, всегда старайтесь использовать правила операций и последовательно решать уравнения.

Практика на примерах

Вот несколько примеров уравнений, которые вы можете решить для тренировки:

Пример 1:

Решите уравнение: 2x + 3 = 9

Решение:

Для начала, вычтите 3 с обеих сторон уравнения:

2x = 6

Затем, разделите обе стороны на 2:

x = 3

Пример 2:

Решите уравнение: 5y — 2 = 13

Решение:

Для начала, добавьте 2 к обеим сторонам уравнения:

5y = 15

Затем, разделите обе стороны на 5:

y = 3

Постепенно решая все больше примеров, вы становитесь более уверенными в решении уравнений и развиваете свои навыки в математике. Не бойтесь экспериментировать и задавать вопросы своему учителю, если вам необходима дополнительная помощь.

Проверка правильности решения

После того, как вы получили ответ на уравнение, важно проверить его правильность. Ведь ошибки могут случаться, и нам нужно быть уверенными в полученном результате.

Для проверки правильности решения, мы подставим ответ обратно в исходное уравнение и убедимся, что обе его части равны друг другу.

Возьмем, например, уравнение: 3x + 5 = 17. Решением этого уравнения будет x = 4. Теперь подставим это значение вместо x в исходное уравнение:

1. 3 * 4 + 5 = 17
2. 12 + 5 = 17
3. 17 = 17

Обе части уравнения равны 17, что значит, что наше решение x = 4 верно.

Таким образом, чтобы убедиться в правильности решения, достаточно подставить его вместо переменной в исходное уравнение и проверить равенство обеих его частей.

Расширение навыков решения уравнений

Один из способов расширить навыки решения уравнений — решение уравнений с переменными в обоих членах. В этом случае уравнение выглядит следующим образом: a + x = b + x. Для решения таких уравнений необходимо применить принципы алгебры, а именно свойство равенства, которое позволяет прибавить или вычесть одно и то же число к обоим членам уравнения.

Еще один способ расширить навыки решения уравнений — решение уравнений с дробями. В этом случае уравнение может содержать дроби как в числителях, так и в знаменателях. Решение таких уравнений требует знания правил работы с дробями, а именно умение приводить дроби к общему знаменателю и производить операции с дробями.

Также можно расширить навыки решения уравнений путем решения систем уравнений. Система уравнений — это набор уравнений, которые решаются одновременно. Для решения систем уравнений необходимо применять различные методы, такие как метод подстановки, метод сложения или вычитания уравнений, метод графического представления и т. д.

Для расширения навыков решения уравнений также полезно решать задачи, в которых требуется составить и решить уравнение. Такие задачи помогут применить полученные знания на практике и развить логическое мышление.

Расширение навыков решения уравнений поможет ученикам справиться с более сложными задачами и развить алгебраическое мышление. Постепенно уровень сложности задач можно увеличивать, что позволит ученикам совершенствоваться и достигать математического успеха.

Полезные советы для успешного решения уравнений

Решение уравнений может показаться сложным заданием, но с правильным подходом и практикой, вы сможете справиться с ними легко. Вот несколько полезных советов, которые помогут вам успешно решать уравнения.

1. Внимательно читайте задачу. Перед тем, как приступить к решению уравнения, внимательно прочитайте задачу и понимайте, что она требует от вас. Выделите ключевые слова и фразы, которые помогут вам определить, какой тип уравнения вам нужно решить.

2. Постепенно раскрывайте уравнение. Постепенно раскрывайте уравнение, выполняя одни и те же операции на обеих сторонах. Используйте законы алгебры для переноса переменных и чисел из одного места в другое. Убедитесь, что вы выполнили одни и те же действия на обеих сторонах уравнения, чтобы сохранить его равенство.

3. Ответ проверяйте. После того, как вы решили уравнение, не забудьте проверить свой ответ, подставив его обратно в исходное уравнение. Убедитесь, что обе стороны уравнения равны друг другу. Если они это не делают, проверьте свои вычисления еще раз.

4. Упражняйтесь. Решение уравнений требует практики. Чем больше уравнений вы решаете, тем легче вам будет справляться с ними. Используйте упражнения и примеры из учебника, а также попросите своего учителя дать вам дополнительные задания для тренировки.

Следуя этим полезным советам, вы сможете успешно решать уравнения и достичь математического успеха. Не забывайте, что практика — ключ к успеху в математике!